Sharing tips on parabolic motion of images in HTML5
Jan 11, 2018 am 10:17 AMThis article mainly introduces some thoughts on the parabolic motion of pictures in h5, and introduces in detail the method of motion along the Bezier curve. It has certain reference value. Interested friends can refer to it. I hope it can Help everyone.
Commonly, objects/pictures move in a parabola or, more accurately, move along a Bezier curve. This is a common requirement in H5 development. So how to quickly calculate the movement path based on the design draft is the first solution for developers. The problem.
The commonly used design draft size for H5 development here is 640 * 1008, so the solution idea based on this size is as follows:
1. First, separate the elements to be displaced in PS Export a png. If the motion route has been planned in the design draft, you also need to export the route as png;
2. Create a new file in AI with the same size as the design draft, and then add the displacement elements Drag it into the file twice. If there is a motion route, also drag it in, as shown below:
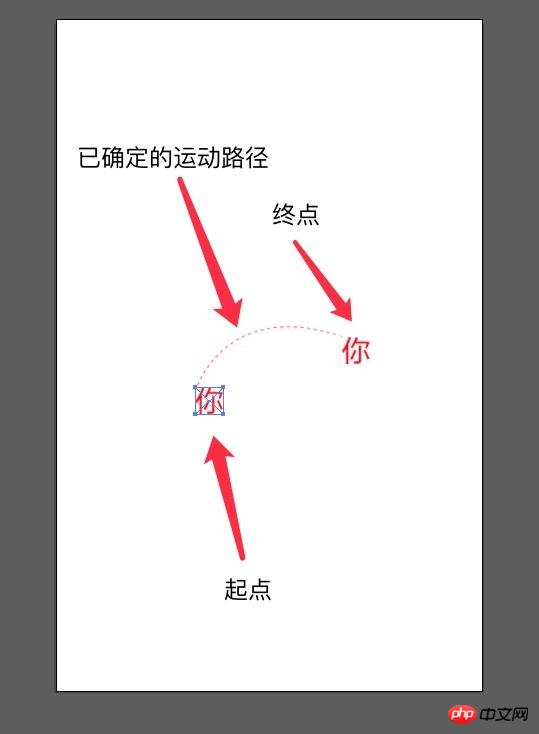
What needs to be paid attention to here is the placement of the displacement image. The starting point and end point of the path should correspond to the moving point of the picture. The corresponding situations are as follows:
There is no deformation processing in the canvas, then the moving point is the upper left corner of the picture
In the canvas, the image has been translated and moved because drawImage(image, sx, sy, sWidth, sHeight, dx, dy is added according to x1 and y1 in translate(x1, y1) , dWidth, dHeight) the final offset of dx and dy.
If the element is positioned through position:absolute and the position is controlled by translate3d(x, y, z) in transform , the offset should be x, y. Generally, in transform, we may imitate left, top and additional margin to control the position of the element, and add an additional translate3D(marginLeftX, marginLeftY, 0) in transform. Also needed Take the value of this margin into consideration.
3. Use the ctrl + r keys to pull out the reference line in AI, and move the element image to pull out its x and y positions, as follows As shown in the picture:
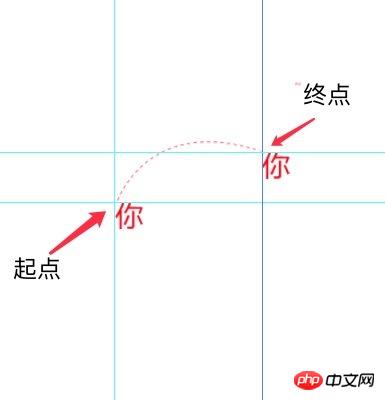
Then select the pen tool, click on the starting point and the end point successively, do not release the mouse after clicking the end point, drag the AI directly and it will automatically add 2 Control points. You can adjust the position of the two control points by moving the mouse to adjust the path generated by the pen tool until it is consistent with the reference line path on the design draft. As shown below:
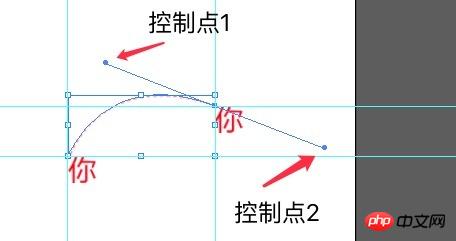
After dragging to the desired position, release the mouse and press Enter to confirm the path. If the outlined path is not what you want, you can continue to drag the control points to make adjustments.
4 , after the adjustment is completed, drag two additional reference lines to the position of control point 1, then open the information panel through the menu bar - window - information, and set the starting point, control point, end point, and the coordinates of the three points respectively. Take it out.
5, calculate the pixel difference between the control point, the end point and the starting point respectively, and calculate the real control point based on the real x, y coordinate values and pixel difference of the picture to be displaced in H5. End point coordinates. Then apply these three coordinate points to the formula.
Copy code
The code is as follows:
var path = getBezierPath([278 + 119, 572 - 32], [ 278 - 4, 572 - 137] , [278 + 119, 572 - 32] , [ 278, 572], 50);
Among them, the parameters are getBezierPath (end point, control point 1, control point 2, starting point, number of movements). If there is no control point 2, directly talk about the end point. Just fill in the coordinates. The final formula of _getBezierPath is as follows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
|
Related recommendations:
Two JSs to realize the parabolic trajectory of the ball Method of movement
Code case for parabolic movement of elastic potential energy animation in JavaScript
The above is the detailed content of Sharing tips on parabolic motion of images in HTML5. For more information, please follow other related articles on the PHP Chinese website!

Hot Article

Hot tools Tags

Hot Article

Hot Article Tags

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)















