
The red-black tree is a type of balanced binary search tree. In order to deeply understand red-black trees, we need to start with binary search trees.
Binary Search Tree (In-depth analysis of Javas implementation of red-black trees (picture) for short) is a binary tree. The value of its left child node is smaller than the value of the parent node, and the value of the right node is larger. Greater than the value of the parent node. Its height determines its search efficiency.
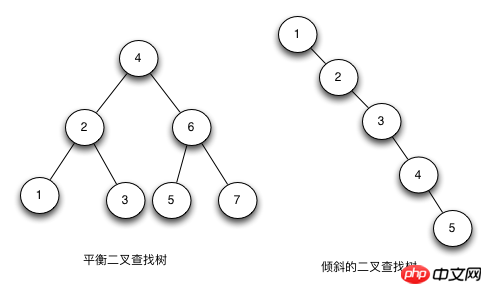
In ideal circumstances, the time complexity of adding, deleting, and modifying a binary search tree is O(logN) (where N is the number of nodes), and in the worst case it is O(N). When its height is logN+1, we say that the binary search tree is balanced.
T key = a search key
Node root = point to the root of a In-depth analysis of Javas implementation of red-black trees (picture)
while(true){
if(root==null){
break;
}
if(root.value.equals(key)){
return root;
}
else if(key.compareTo(root.value)<0){
root = root.left;
}
else{
root = root.right;
}
}
return null;As can be seen from the program, when In-depth analysis of Javas implementation of red-black trees (picture) searches, it first compares with the current node:
If equal, return the current node;
If it is less than the current node, continue to search for the left node of the current node;
If it is greater than the current node, continue to search for the right node of the current node.
Until the current node pointer is empty or the corresponding node is found, the program search ends.
Node node = create a new node with specify value
Node root = point the root node of a In-depth analysis of Javas implementation of red-black trees (picture)
Node parent = null;
//find the parent node to append the new node
while(true){
if(root==null)break;
parent = root;
if(node.value.compareTo(root.value)<=0){
root = root.left;
}else{
root = root.right;
}
}
if(parent!=null){
if(node.value.compareTo(parent.value)<=0){//append to left
parent.left = node;
}else{//append to right
parent.right = node;
}
}The insertion operation first finds the parent node of the node to be inserted through a loop. The logic of finding the parent node is the same, which is smaller than the size and goes to the left. The big one goes to the right. After finding the parent node, compare the parent node, the smaller one is inserted into the left node of the parent node, and the larger one is inserted into the right node of the parent node.
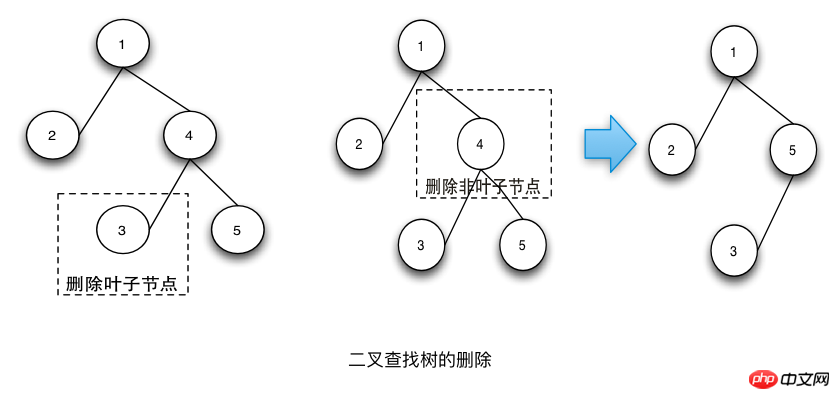
The steps for deletion operation are as follows:
Find the node to be deleted.
If the node to be deleted is a leaf node, delete it directly.
If the node to be deleted is not a leaf node, first find the successor node of the in-order traversal of the node to be deleted, replace the value of the node to be deleted with the value of the successor node, and then Delete successor nodes.
The main problem with In-depth analysis of Javas implementation of red-black trees (picture) is that when numbers are inserted, they will cause the tree to tilt. Different The insertion order will cause the height of the tree to be different, and the height of the tree directly affects the search efficiency of the tree. The ideal height is logN. The worst case is that all nodes are on a diagonal line, and the height of such a tree is N.
Based on the existing problems of In-depth analysis of Javas implementation of red-black trees (picture), a new tree - Balanced Binary Search Tree (Balanced In-depth analysis of Javas implementation of red-black trees (picture)) was created. When inserting and deleting, the balanced tree will maintain the height at logN through rotation operations. Two representative balanced trees are AVL trees and red-black trees. Due to the complex implementation and poor insertion and deletion performance of AVL trees, their application in actual environments is not as good as red-black trees.
Red-Black Tree (hereinafter referred to as RBTree) has a wide range of practical applications, such as the completely fair scheduler in the Linux kernel, high-precision timers, ext3 file systems, etc., in various languages Function libraries such as Java's TreeMap and TreeSet, C++ STL's map, multimap, multiset, etc.
RBTree is also one of the most commonly used persistent data structures in functional languages and also plays an important role in computational geometry. It is worth mentioning that the performance of HashMap implementation in Java 8 has been improved by replacing linked lists with RBTree.
The definition of RBTree is as follows:
Any node has a color, black or red
The root node is black
There cannot be two consecutive red nodes between the parent and child nodes
Any node goes down To traverse to the leaf nodes of its descendants, the number of black nodes passed must be equal
Empty nodes are considered black
Data structure It is expressed as follows:
class Node<T>{
public T value;
public Node<T> parent;
public boolean isRed;
public Node<T> left;
public Node<T> right;
}RBTree is still a In-depth analysis of Javas implementation of red-black trees (picture) tree in theory, but it will maintain the balance of the tree when inserting and deleting In-depth analysis of Javas implementation of red-black trees (picture) operations, that is, ensuring that the height of the tree is [logN,logN+1] (Theoretically, in extreme cases, the height of RBTree can reach 2*logN, but in practice it is difficult to encounter). In this way, the search time complexity of RBTree always remains at O(logN) and is close to the ideal In-depth analysis of Javas implementation of red-black trees (picture). The time complexity of RBTree's deletion and insertion operations is also O(logN). The search operation of RBTree is the search operation of In-depth analysis of Javas implementation of red-black trees (picture).
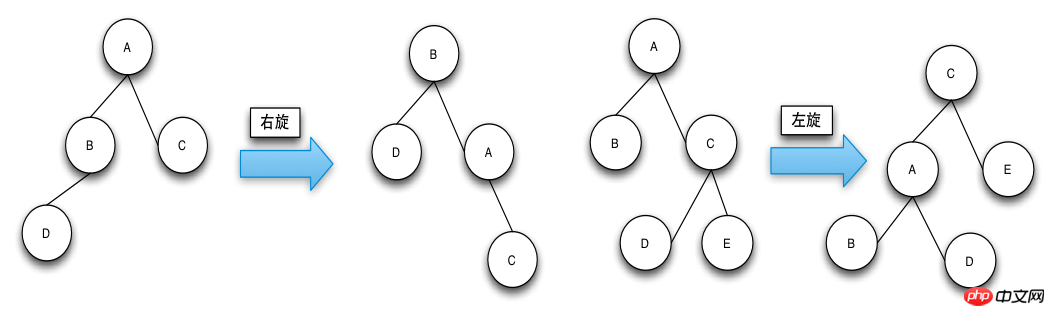
The purpose of rotation operation (Rotate) is to make the node color conform to the definition and make the height of RBTree reach balance.
Rotate is divided into left-rotate (left-hand rotation) and right-rotate (right-hand rotation). The method of distinguishing left-hand rotation and right-hand rotation is: the node to be rotated ascends from the left to the parent node, which means right rotation, and the node to be rotated moves from the right to the parent node. Ascending to the parent node is a left turn.
RBTree search operation is the same as In-depth analysis of Javas implementation of red-black trees (picture) search operation. Please refer to In-depth analysis of Javas implementation of red-black trees (picture)'s lookup operation code.
The insertion method of RBTree is the same as that of In-depth analysis of Javas implementation of red-black trees (picture). However, after the insertion, the tree may be unbalanced. At this time, the tree needs to be rotated and Color fix (referred to as insertion fix here) so that it conforms to the definition of RBTree.
The newly inserted node is red. If the insertion repair operation encounters a parent node whose color is black, the repair operation ends. In other words, the repair operation needs to be inserted only when the parent node is a red node.
The insertion and repair operation is divided into the following three situations, and the parent nodes of the newly inserted nodes are all red:
The uncle node is also red.
The uncle node is empty, and the grandparent node, parent node and new node are on a slash.
The uncle node is empty, and the grandparent node, parent node and new node are not on a slash.
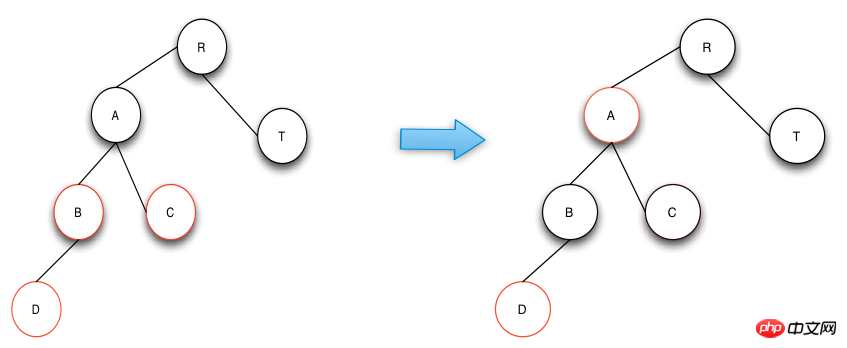
The operation of case 1 is to swap the colors of the parent node, uncle node and grandparent node, which conforms to the definition of RBTree. That is to say, a high degree of balance is maintained, and the color after repair also complies with the third and fourth items defined by RBTree. In the figure below, node A becomes a new node after the operation is completed. If the parent node of node A is not black, continue the repair operation.
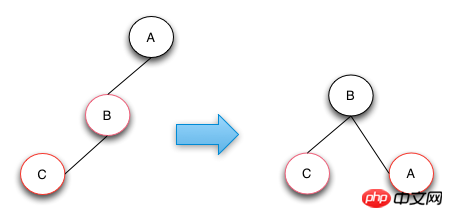
The operation of case 2 is to rotate node B right and exchange colors with parent node A. Through this repair operation, the height and color of RBTree conform to the definition of red-black tree. If nodes B and C are both right nodes, just change the operation to left rotation.
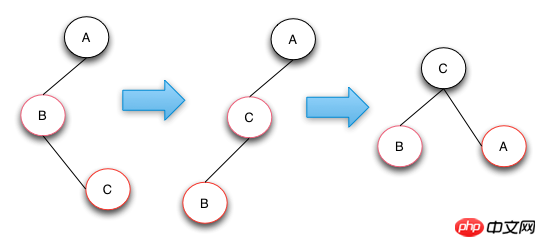
The operation of case 3 is to rotate the C node left, so that it is converted from case 3 to case 2, and then for Just perform operation processing in case 2. The case 2 operation performs a right-turn operation and color swap to achieve the goal. If the structure of the tree is the mirror structure of the figure below, you only need to change the corresponding left-hand rotation to right-hand rotation, and the right-hand rotation to left-hand rotation.
The repair operation after the insertion is a backtracking operation to the root node. Once the nodes involved are in line with the red-black tree Definition, the repair operation is completed. The reason for backtracing upward is that the case 1 operation will change the color of the parent node, uncle node and grandfather node, which may cause the grandfather node to be unbalanced (red-black tree definition 3). At this time, it is necessary to adjust the grandfather node as the starting point (backtracking upward).
If the grandfather node still encounters its grandfather color problem after adjustment, the operation will continue to backtrack upward until the root node. By definition, the root node is always black. In the upward tracing process, adjustments are made for the three inserted situations. Until the definition of a red-black tree is met. Until all involved nodes meet the definition of a red-black tree, the repair operation ends.
If the corresponding operation in the above 3 situations is on the right subtree, just perform the corresponding mirror operation.
The deletion operation first needs to be done by the In-depth analysis of Javas implementation of red-black trees (picture) deletion operation. The deletion operation will delete the corresponding node. If it is a leaf node, it will be deleted directly. If it is a non-leaf node, it will be deleted. Replace the position of the node to be deleted with the corresponding successor node of the in-order traversal. After deletion, you need to perform a deletion and repair operation to make the tree conform to the definition of a red-black tree, and the height of the red-black tree that meets the definition is balanced.
The deletion and repair operation is completed when the deleted node is a red node or reaches the root node.
The deletion and repair operation is only for deleting black nodes. When the black nodes are deleted, the entire tree will not comply with the fourth definition of RBTree. What needs to be done is to second the black nodes from the sibling nodes. If the sibling nodes have no black nodes to borrow, we can only trace back up and subtract one from the number of black nodes at each level to make the entire tree conform to the red node. Black tree definition.
The overall idea of the deletion operation is to second the black nodes from the sibling nodes to maintain the local balance of the tree. If the local balance is achieved, it depends on whether the overall tree is balanced. If it is unbalanced, it will be adjusted upward retrospectively. .
The deletion and repair operation is divided into four situations (after deleting the black node):
The sibling node of the node to be deleted is a red node.
The sibling nodes of the node to be deleted are black nodes, and the child nodes of the sibling nodes are all black.
The sibling node of the node to be adjusted is a black node, and the left child node of the sibling node is red, and the right node is black (the sibling node is on the right). If the sibling node On the left, the right child node of the sibling node is red and the left node is black.
待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
由于兄弟节点是红色节点的时候,无法借调黑节点,所以需要将兄弟节点提升到父节点,由于兄弟节点是红色的,根据RBTree的定义,兄弟节点的子节点是黑色的,就可以从它的子节点借调了。
case 1这样转换之后就会变成后面的case 2,case 3,或者case 4进行处理了。上升操作需要对C做一个左旋操作,如果是镜像结构的树只需要做对应的右旋操作即可。
之所以要做case 1操作是因为兄弟节点是红色的,无法借到一个黑节点来填补删除的黑节点。
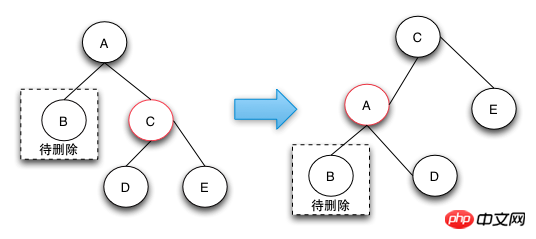
case 2的删除操作是由于兄弟节点可以消除一个黑色节点,因为兄弟节点和兄弟节点的子节点都是黑色的,所以可以将兄弟节点变红,这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点,继续向上调整,直到整颗树的颜色符合RBTree的定义为止。
case 2这种情况下之所以要将兄弟节点变红,是因为如果把兄弟节点借调过来,会导致兄弟的结构不符合RBTree的定义,这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后,达到了局部的平衡了,但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点,接着进行修复操作。
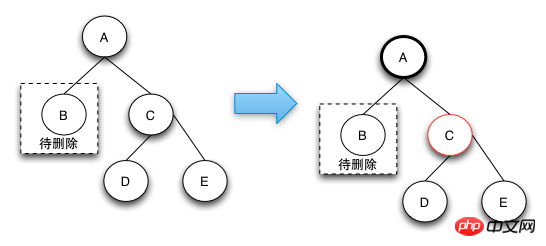
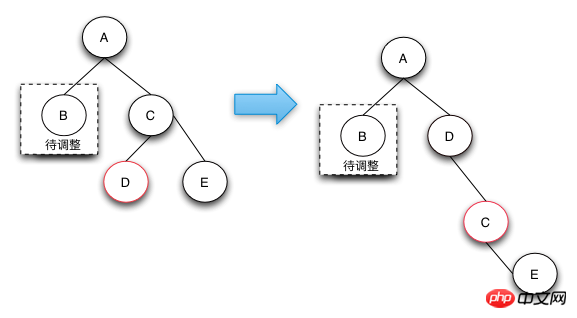
case 3的删除操作是一个中间步骤,它的目的是将左边的红色节点借调过来,这样就可以转换成case 4状态了,在case 4状态下可以将D,E节点都阶段过来,通过将两个节点变成黑色来保证红黑树的整体平衡。
之所以说case-3是一个中间状态,是因为根据红黑树的定义来说,下图并不是平衡的,他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况,是因为可以通过借用侄子节点的红色,变成黑色来符合红黑树定义4.
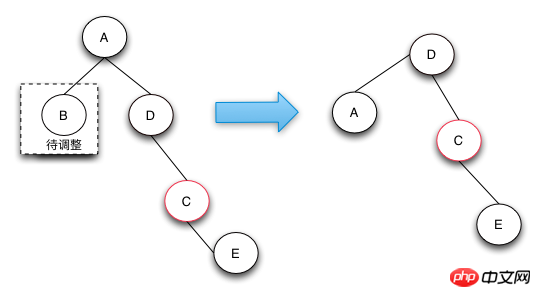
Case 4的操作是真正的节点借调操作,通过将兄弟节点以及兄弟节点的右节点借调过来,并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的,这样的话,整棵树还是符合RBTree的定义的。
Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑,且子节点不全部为黑,才有可能借调到两个节点来做黑节点使用,从而保持整棵树都符合红黑树的定义。
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。
public class RBTreeNode<T extends Comparable<T>> {
private T value;//node value
private RBTreeNode<T> left;//left child pointer
private RBTreeNode<T> right;//right child pointer
private RBTreeNode<T> parent;//parent pointer
private boolean red;//color is red or not red
public RBTreeNode(){}
public RBTreeNode(T value){this.value=value;}
public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}
public T getValue() {
return value;
}
void setValue(T value) {
this.value = value;
}
RBTreeNode<T> getLeft() {
return left;
}
void setLeft(RBTreeNode<T> left) {
this.left = left;
}
RBTreeNode<T> getRight() {
return right;
}
void setRight(RBTreeNode<T> right) {
this.right = right;
}
RBTreeNode<T> getParent() {
return parent;
}
void setParent(RBTreeNode<T> parent) {
this.parent = parent;
}
boolean isRed() {
return red;
}
boolean isBlack(){
return !red;
}
/**
* is leaf node
**/
boolean isLeaf(){
return left==null && right==null;
}
void setRed(boolean red) {
this.red = red;
}
void makeRed(){
red=true;
}
void makeBlack(){
red=false;
}
@Override
public String toString(){
return value.toString();
}
}
public class RBTree<T extends Comparable<T>> {
private final RBTreeNode<T> root;
//node number
private java.util.concurrent.atomic.AtomicLong size =
new java.util.concurrent.atomic.AtomicLong(0);
//in overwrite mode,all node's value can not has same value
//in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
private volatile boolean overrideMode=true;
public RBTree(){
this.root = new RBTreeNode<T>();
}
public RBTree(boolean overrideMode){
this();
this.overrideMode=overrideMode;
}
public boolean isOverrideMode() {
return overrideMode;
}
public void setOverrideMode(boolean overrideMode) {
this.overrideMode = overrideMode;
}
/**
* number of tree number
* @return
*/
public long getSize() {
return size.get();
}
/**
* get the root node
* @return
*/
private RBTreeNode<T> getRoot(){
return root.getLeft();
}
/**
* add value to a new node,if this value exist in this tree,
* if value exist,it will return the exist value.otherwise return null
* if override mode is true,if value exist in the tree,
* it will override the old value in the tree
*
* @param value
* @return
*/
public T addNode(T value){
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* find the value by give value(include key,key used for search,
* other field is not used,@see compare method).if this value not exist return null
* @param value
* @return
*/
public T find(T value){
RBTreeNode<T> dataRoot = getRoot();
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
dataRoot = dataRoot.getRight();
}else if(cmp>0){
dataRoot = dataRoot.getLeft();
}else{
return dataRoot.getValue();
}
}
return null;
}
/**
* remove the node by give value,if this value not exists in tree return null
* @param value include search key
* @return the value contain in the removed node
*/
public T remove(T value){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
parent = dataRoot;
dataRoot = dataRoot.getRight();
}else if(cmp>0){
parent = dataRoot;
dataRoot = dataRoot.getLeft();
}else{
if(dataRoot.getRight()!=null){
RBTreeNode<T> min = removeMin(dataRoot.getRight());
//x used for fix color balance
RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
boolean isParent = min.getRight()==null;
min.setLeft(dataRoot.getLeft());
setParent(dataRoot.getLeft(),min);
if(parent.getLeft()==dataRoot){
parent.setLeft(min);
}else{
parent.setRight(min);
}
setParent(min,parent);
boolean curMinIsBlack = min.isBlack();
//inherit dataRoot's color
min.setRed(dataRoot.isRed());
if(min!=dataRoot.getRight()){
min.setRight(dataRoot.getRight());
setParent(dataRoot.getRight(),min);
}
//remove a black node,need fix color
if(curMinIsBlack){
if(min!=dataRoot.getRight()){
fixRemove(x,isParent);
}else if(min.getRight()!=null){
fixRemove(min.getRight(),false);
}else{
fixRemove(min,true);
}
}
}else{
setParent(dataRoot.getLeft(),parent);
if(parent.getLeft()==dataRoot){
parent.setLeft(dataRoot.getLeft());
}else{
parent.setRight(dataRoot.getLeft());
}
//current node is black and tree is not empty
if(dataRoot.isBlack() && !(root.getLeft()==null)){
RBTreeNode<T> x = dataRoot.getLeft()==null
? parent :dataRoot.getLeft();
boolean isParent = dataRoot.getLeft()==null;
fixRemove(x,isParent);
}
}
setParent(dataRoot,null);
dataRoot.setLeft(null);
dataRoot.setRight(null);
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
size.decrementAndGet();
return dataRoot.getValue();
}
}
return null;
}
/**
* fix remove action
* @param node
* @param isParent
*/
private void fixRemove(RBTreeNode<T> node,boolean isParent){
RBTreeNode<T> cur = isParent ? null : node;
boolean isRed = isParent ? false : node.isRed();
RBTreeNode<T> parent = isParent ? node : node.getParent();
while(!isRed && !isRoot(cur)){
RBTreeNode<T> sibling = getSibling(cur,parent);
//sibling is not null,due to before remove tree color is balance
//if cur is a left node
boolean isLeft = parent.getRight()==sibling;
if(sibling.isRed() && !isLeft){//case 1
//cur in right
parent.makeRed();
sibling.makeBlack();
rotateRight(parent);
}else if(sibling.isRed() && isLeft){
//cur in left
parent.makeRed();
sibling.makeBlack();
rotateLeft(parent);
}else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
sibling.makeRed();
cur = parent;
isRed = cur.isRed();
parent=parent.getParent();
}else if(isLeft && !isBlack(sibling.getLeft())
&& isBlack(sibling.getRight())){//case 3
sibling.makeRed();
sibling.getLeft().makeBlack();
rotateRight(sibling);
}else if(!isLeft && !isBlack(sibling.getRight())
&& isBlack(sibling.getLeft()) ){
sibling.makeRed();
sibling.getRight().makeBlack();
rotateLeft(sibling);
}else if(isLeft && !isBlack(sibling.getRight())){//case 4
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getRight().makeBlack();
rotateLeft(parent);
cur=getRoot();
}else if(!isLeft && !isBlack(sibling.getLeft())){
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getLeft().makeBlack();
rotateRight(parent);
cur=getRoot();
}
}
if(isRed){
cur.makeBlack();
}
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
}
//get sibling node
private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
parent = node==null ? parent : node.getParent();
if(node==null){
return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
}
if(node==parent.getLeft()){
return parent.getRight();
}else{
return parent.getLeft();
}
}
private boolean isBlack(RBTreeNode<T> node){
return node==null || node.isBlack();
}
private boolean isRoot(RBTreeNode<T> node){
return root.getLeft() == node && node.getParent()==null;
}
/**
* find the successor node
* @param node current node's right node
* @return
*/
private RBTreeNode<T> removeMin(RBTreeNode<T> node){
//find the min node
RBTreeNode<T> parent = node;
while(node!=null && node.getLeft()!=null){
parent = node;
node = node.getLeft();
}
//remove min node
if(parent==node){
return node;
}
parent.setLeft(node.getRight());
setParent(node.getRight(),parent);
//don't remove right pointer,it is used for fixed color balance
//node.setRight(null);
return node;
}
private T addNode(RBTreeNode<T> node){
node.setLeft(null);
node.setRight(null);
node.setRed(true);
setParent(node,null);
if(root.getLeft()==null){
root.setLeft(node);
//root node is black
node.setRed(false);
size.incrementAndGet();
}else{
RBTreeNode<T> x = findParentNode(node);
int cmp = x.getValue().compareTo(node.getValue());
if(this.overrideMode && cmp==0){
T v = x.getValue();
x.setValue(node.getValue());
return v;
}else if(cmp==0){
//value exists,ignore this node
return x.getValue();
}
setParent(node,x);
if(cmp>0){
x.setLeft(node);
}else{
x.setRight(node);
}
fixInsert(node);
size.incrementAndGet();
}
return null;
}
/**
* find the parent node to hold node x,if parent value equals x.value return parent.
* @param x
* @return
*/
private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> child = dataRoot;
while(child!=null){
int cmp = child.getValue().compareTo(x.getValue());
if(cmp==0){
return child;
}
if(cmp>0){
dataRoot = child;
child = child.getLeft();
}else if(cmp<0){
dataRoot = child;
child = child.getRight();
}
}
return dataRoot;
}
/**
* red black tree insert fix.
* @param x
*/
private void fixInsert(RBTreeNode<T> x){
RBTreeNode<T> parent = x.getParent();
while(parent!=null && parent.isRed()){
RBTreeNode<T> uncle = getUncle(x);
if(uncle==null){//need to rotate
RBTreeNode<T> ancestor = parent.getParent();
//ancestor is not null due to before before add,tree color is balance
if(parent == ancestor.getLeft()){
boolean isRight = x == parent.getRight();
if(isRight){
rotateLeft(parent);
}
rotateRight(ancestor);
if(isRight){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}else{
boolean isLeft = x == parent.getLeft();
if(isLeft){
rotateRight(parent);
}
rotateLeft(ancestor);
if(isLeft){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}
}else{//uncle is red
parent.setRed(false);
uncle.setRed(false);
parent.getParent().setRed(true);
x=parent.getParent();
parent = x.getParent();
}
}
getRoot().makeBlack();
getRoot().setParent(null);
}
/**
* get uncle node
* @param node
* @return
*/
private RBTreeNode<T> getUncle(RBTreeNode<T> node){
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> ancestor = parent.getParent();
if(ancestor==null){
return null;
}
if(parent == ancestor.getLeft()){
return ancestor.getRight();
}else{
return ancestor.getLeft();
}
}
private void rotateLeft(RBTreeNode<T> node){
RBTreeNode<T> right = node.getRight();
if(right==null){
throw new java.lang.IllegalStateException("right node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setRight(right.getLeft());
setParent(right.getLeft(),node);
right.setLeft(node);
setParent(node,right);
if(parent==null){//node pointer to root
//right raise to root node
root.setLeft(right);
setParent(right,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(right);
}else{
parent.setRight(right);
}
//right.setParent(parent);
setParent(right,parent);
}
}
private void rotateRight(RBTreeNode<T> node){
RBTreeNode<T> left = node.getLeft();
if(left==null){
throw new java.lang.IllegalStateException("left node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setLeft(left.getRight());
setParent(left.getRight(),node);
left.setRight(node);
setParent(node,left);
if(parent==null){
root.setLeft(left);
setParent(left,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(left);
}else{
parent.setRight(left);
}
setParent(left,parent);
}
}
private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
if(node!=null){
node.setParent(parent);
if(parent==root){
node.setParent(null);
}
}
}
/**
* debug method,it used print the given node and its children nodes,
* every layer output in one line
* @param root
*/
public void printTree(RBTreeNode<T> root){
java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
if(root==null){
return ;
}
queue.add(root);
boolean firstQueue = true;
while(!queue.isEmpty() || !queue2.isEmpty()){
java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
RBTreeNode<T> n = q.poll();
if(n!=null){
String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft()
? " LE" : " RI");
String pstr = n.getParent()==null ? "" : n.getParent().toString();
String cstr = n.isRed()?"R":"B";
cstr = n.getParent()==null ? cstr : cstr+" ";
System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
if(n.getLeft()!=null){
(firstQueue ? queue2 : queue).add(n.getLeft());
}
if(n.getRight()!=null){
(firstQueue ? queue2 : queue).add(n.getRight());
}
}else{
System.out.println();
firstQueue = !firstQueue;
}
}
}
public static void main(String[] args) {
RBTree<String> bst = new RBTree<String>();
bst.addNode("d");
bst.addNode("d");
bst.addNode("c");
bst.addNode("c");
bst.addNode("b");
bst.addNode("f");
bst.addNode("a");
bst.addNode("e");
bst.addNode("g");
bst.addNode("h");
bst.remove("c");
bst.printTree(bst.getRoot());
}
}代码调试的时候,printTree输出格式如下:
d(B) b(B d LE) g(R d RI) a(R b LE) e(B g LE) h(B g RI) f(R e RI)
括号左边表示元素的内容。括号内的第一个元素表示颜色,B表示black,R表示red;第二个元素表示父元素的值;第三个元素表示左右,LE表示在父元素的左边。RI表示在父元素的右边。
第一个元素d是root节点,由于它没有父节点,所以括号内只有一个元素。
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。
The above is the detailed content of In-depth analysis of Java's implementation of red-black trees (picture). For more information, please follow other related articles on the PHP Chinese website!




