 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 JavaScript implements pre-order, in-order and post-order traversal methods of binary trees
JavaScript implements pre-order, in-order and post-order traversal methods of binary trees
JavaScript implements pre-order, in-order and post-order traversal methods of binary trees
This article mainly introduces the JavaScript implementation of pre-order, in-order and post-order traversal methods of binary trees. It summarizes and analyzes the implementation methods of pre-order, in-order and post-order traversal of binary trees in JavaScript and related operation precautions in the form of examples. What is needed Friends can refer to it, I hope it can help everyone.
The example of this article describes the JavaScript implementation of pre-order, in-order and post-order traversal methods of binary trees. I share it with you for your reference. The details are as follows:
When I was learning data structure before, I learned the pre-order, in-order and post-order traversal methods of binary trees and implemented them in C language. The following is implemented in js Three types of traversal of binary trees, and the traversal process is shown in the form of animation.
The entire traversal process still uses recursive thinking. The principle is very crude and simple.
Function of pre-order traversal:
function preOrder(node){
if(!(node==null)){
pList.push(node);
preOrder(node.firstElementChild);
preOrder(node.lastElementChild);
}
}中Function of in-order traversal:
function inOrder(node) {
if (!(node == null)) {
inOrder(node.firstElementChild);
pList.push(node);
inOrder(node.lastElementChild);
}
}Function of post-order traversal:
function postOrder(node) {
if (!(node == null)) {
postOrder(node.firstElementChild);
postOrder(node.lastElementChild);
pList.push(node);
}
}Color change function:
function changeColor(){
var i=0;
pList[i].style.backgroundColor = 'blue';
timer=setInterval(function(argument){
i++;
if(i<pList.length){
pList[i-1].style.backgroundColor="#fff";
pList[i].style.backgroundColor="blue";
}
else{
pList[pList.length-1].style.backgroundColor="#fff";
}
},500)
}The core code is as above. I originally wanted to write depth-first traversal and breadth-first traversal. Later it was discovered that depth-first traversal of a binary tree is the same as pre-order traversal. I will summarize the BFS and DFS of trees another day.
The entire code is as follows:
<!DOCTYPE html>
<html>
<head lang="en">
<meta charset="UTF-8">
<title></title>
<style>
.root{
display: flex;
padding: 20px;
width: 1000px;
height: 300px;border: 1px solid #000000;
margin: 100px auto;
margin-bottom: 10px;
justify-content: space-between;
}
.child_1{
display: flex;
padding: 20px;
width: 450px;
height: 260px;border: 1px solid red;
justify-content: space-between;
}
.child_2{
display: flex;
padding: 20px;
width: 170px;
height: 220px;border: 1px solid green;
justify-content: space-between;
}
.child_3{
display: flex;
padding: 20px;
width: 35px;
height: 180px;border: 1px solid blue;
justify-content: space-between;
}
input{
margin-left: 100px;
width: 60px;
height: 40px;
font:20px italic;
}
</style>
</head>
<body>
<p class="root">
<p class="child_1">
<p class="child_2">
<p class="child_3"></p>
<p class="child_3"></p>
</p>
<p class="child_2">
<p class="child_3"></p>
<p class="child_3"></p>
</p>
</p>
<p class="child_1">
<p class="child_2">
<p class="child_3"></p>
<p class="child_3"></p>
</p>
<p class="child_2">
<p class="child_3"></p>
<p class="child_3"></p>
</p>
</p>
</p>
<input type="button" value="先序">
<input type="button" value="中序">
<input type="button" value="后序">
<script type="text/javascript" src="遍历.js"></script>
</body>
</html>js:
/**
* Created by hp on 2016/12/22.
*/
var btn = document.getElementsByTagName('input'),
preBtn = btn[0],
inBtn = btn[1],
postBtn = btn[2],
treeRoot = document.getElementsByClassName('root')[0],
pList = [],
timer = null;
window.onload=function(){
preBtn.onclick = function () {
reset();
preOrder(treeRoot);
changeColor();
}
inBtn.onclick = function () {
reset();
inOrder(treeRoot);
changeColor();
}
postBtn.onclick = function () {
reset();
postOrder(treeRoot);
changeColor();
}
}
/*先序遍历*/
function preOrder(node){
if(!(node==null)){
pList.push(node);
preOrder(node.firstElementChild);
preOrder(node.lastElementChild);
}
}
/*中序遍历*/
function inOrder(node) {
if (!(node == null)) {
inOrder(node.firstElementChild);
pList.push(node);
inOrder(node.lastElementChild);
}
}
/*后序遍历*/
function postOrder(node) {
if (!(node == null)) {
postOrder(node.firstElementChild);
postOrder(node.lastElementChild);
pList.push(node);
}
}
/*颜色变化函数*/
function changeColor(){
var i=0;
pList[i].style.backgroundColor = 'blue';
timer=setInterval(function(argument){
i++;
if(i<pList.length){
pList[i-1].style.backgroundColor="#fff";
pList[i].style.backgroundColor="blue";
}
else{
pList[pList.length-1].style.backgroundColor="#fff";
}
},500)
}
function reset(){
pList=[];
clearInterval(timer);
var ps=document.getElementsByTagName("p");
for(var i=0;iCopy after login It can be seen that the binary tree Traversing thoughts is the same. I used to regard JS as a language for writing various special effects, but now it has always been too naive.
Related recommendations:
Detailed explanation of the definition method of complete binary tree in php
Implementation method of Java minimum binary tree heap sorting
The above is the detailed content of JavaScript implements pre-order, in-order and post-order traversal methods of binary trees. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1663
1663
 14
14
 1420
1420
 52
52
 1315
1315
 25
25
 1266
1266
 29
29
 1239
1239
 24
24
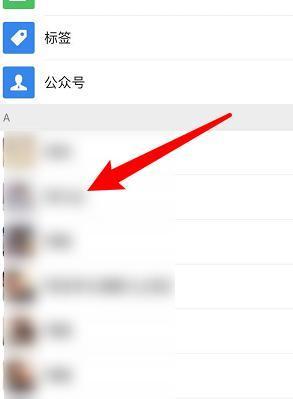 How to recover deleted contacts on WeChat (simple tutorial tells you how to recover deleted contacts)
May 01, 2024 pm 12:01 PM
How to recover deleted contacts on WeChat (simple tutorial tells you how to recover deleted contacts)
May 01, 2024 pm 12:01 PM
Unfortunately, people often delete certain contacts accidentally for some reasons. WeChat is a widely used social software. To help users solve this problem, this article will introduce how to retrieve deleted contacts in a simple way. 1. Understand the WeChat contact deletion mechanism. This provides us with the possibility to retrieve deleted contacts. The contact deletion mechanism in WeChat removes them from the address book, but does not delete them completely. 2. Use WeChat’s built-in “Contact Book Recovery” function. WeChat provides “Contact Book Recovery” to save time and energy. Users can quickly retrieve previously deleted contacts through this function. 3. Enter the WeChat settings page and click the lower right corner, open the WeChat application "Me" and click the settings icon in the upper right corner to enter the settings page.
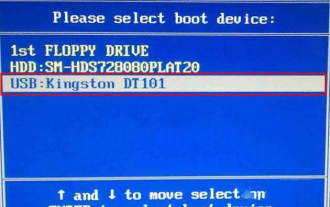 How to enter bios on Colorful motherboard? Teach you two methods
Mar 13, 2024 pm 06:01 PM
How to enter bios on Colorful motherboard? Teach you two methods
Mar 13, 2024 pm 06:01 PM
Colorful motherboards enjoy high popularity and market share in the Chinese domestic market, but some users of Colorful motherboards still don’t know how to enter the bios for settings? In response to this situation, the editor has specially brought you two methods to enter the colorful motherboard bios. Come and try it! Method 1: Use the U disk startup shortcut key to directly enter the U disk installation system. The shortcut key for the Colorful motherboard to start the U disk with one click is ESC or F11. First, use Black Shark Installation Master to create a Black Shark U disk boot disk, and then turn on the computer. When you see the startup screen, continuously press the ESC or F11 key on the keyboard to enter a window for sequential selection of startup items. Move the cursor to the place where "USB" is displayed, and then
 How to write a novel in the Tomato Free Novel app. Share the tutorial on how to write a novel in Tomato Novel.
Mar 28, 2024 pm 12:50 PM
How to write a novel in the Tomato Free Novel app. Share the tutorial on how to write a novel in Tomato Novel.
Mar 28, 2024 pm 12:50 PM
Tomato Novel is a very popular novel reading software. We often have new novels and comics to read in Tomato Novel. Every novel and comic is very interesting. Many friends also want to write novels. Earn pocket money and edit the content of the novel you want to write into text. So how do we write the novel in it? My friends don’t know, so let’s go to this site together. Let’s take some time to look at an introduction to how to write a novel. Share the Tomato novel tutorial on how to write a novel. 1. First open the Tomato free novel app on your mobile phone and click on Personal Center - Writer Center. 2. Jump to the Tomato Writer Assistant page - click on Create a new book at the end of the novel.
 The secret of hatching mobile dragon eggs is revealed (step by step to teach you how to successfully hatch mobile dragon eggs)
May 04, 2024 pm 06:01 PM
The secret of hatching mobile dragon eggs is revealed (step by step to teach you how to successfully hatch mobile dragon eggs)
May 04, 2024 pm 06:01 PM
Mobile games have become an integral part of people's lives with the development of technology. It has attracted the attention of many players with its cute dragon egg image and interesting hatching process, and one of the games that has attracted much attention is the mobile version of Dragon Egg. To help players better cultivate and grow their own dragons in the game, this article will introduce to you how to hatch dragon eggs in the mobile version. 1. Choose the appropriate type of dragon egg. Players need to carefully choose the type of dragon egg that they like and suit themselves, based on the different types of dragon egg attributes and abilities provided in the game. 2. Upgrade the level of the incubation machine. Players need to improve the level of the incubation machine by completing tasks and collecting props. The level of the incubation machine determines the hatching speed and hatching success rate. 3. Collect the resources required for hatching. Players need to be in the game
 Recommended: Excellent JS open source face detection and recognition project
Apr 03, 2024 am 11:55 AM
Recommended: Excellent JS open source face detection and recognition project
Apr 03, 2024 am 11:55 AM
Face detection and recognition technology is already a relatively mature and widely used technology. Currently, the most widely used Internet application language is JS. Implementing face detection and recognition on the Web front-end has advantages and disadvantages compared to back-end face recognition. Advantages include reducing network interaction and real-time recognition, which greatly shortens user waiting time and improves user experience; disadvantages include: being limited by model size, the accuracy is also limited. How to use js to implement face detection on the web? In order to implement face recognition on the Web, you need to be familiar with related programming languages and technologies, such as JavaScript, HTML, CSS, WebRTC, etc. At the same time, you also need to master relevant computer vision and artificial intelligence technologies. It is worth noting that due to the design of the Web side
 Summary of methods to obtain administrator rights in Win11
Mar 09, 2024 am 08:45 AM
Summary of methods to obtain administrator rights in Win11
Mar 09, 2024 am 08:45 AM
A summary of how to obtain Win11 administrator rights. In the Windows 11 operating system, administrator rights are one of the very important permissions that allow users to perform various operations on the system. Sometimes, we may need to obtain administrator rights to complete some operations, such as installing software, modifying system settings, etc. The following summarizes some methods for obtaining Win11 administrator rights, I hope it can help you. 1. Use shortcut keys. In Windows 11 system, you can quickly open the command prompt through shortcut keys.
 Detailed explanation of Oracle version query method
Mar 07, 2024 pm 09:21 PM
Detailed explanation of Oracle version query method
Mar 07, 2024 pm 09:21 PM
Detailed explanation of Oracle version query method Oracle is one of the most popular relational database management systems in the world. It provides rich functions and powerful performance and is widely used in enterprises. In the process of database management and development, it is very important to understand the version of the Oracle database. This article will introduce in detail how to query the version information of the Oracle database and give specific code examples. Query the database version of the SQL statement in the Oracle database by executing a simple SQL statement
 How to set font size on mobile phone (easily adjust font size on mobile phone)
May 07, 2024 pm 03:34 PM
How to set font size on mobile phone (easily adjust font size on mobile phone)
May 07, 2024 pm 03:34 PM
Setting font size has become an important personalization requirement as mobile phones become an important tool in people's daily lives. In order to meet the needs of different users, this article will introduce how to improve the mobile phone use experience and adjust the font size of the mobile phone through simple operations. Why do you need to adjust the font size of your mobile phone - Adjusting the font size can make the text clearer and easier to read - Suitable for the reading needs of users of different ages - Convenient for users with poor vision to use the font size setting function of the mobile phone system - How to enter the system settings interface - In Find and enter the "Display" option in the settings interface - find the "Font Size" option and adjust it. Adjust the font size with a third-party application - download and install an application that supports font size adjustment - open the application and enter the relevant settings interface - according to the individual



