The concept of binary tree
Binary Tree is a finite set of n (n>=0) nodes. The set is either an empty set (empty binary tree), or it consists of a root node and two mutually disjoint trees. It is a binary tree consisting of the left subtree and the right subtree of the root node.
Characteristics of binary trees
Each node has at most two subtrees, so there is no node with degree greater than 2 in the binary tree. Each node in the binary tree is an object, and each data node has three pointers, which are pointers to the parent, left child, and right child. Each node is connected to each other through pointers. The relationship between connected pointers is a parent-child relationship.
Definition of binary tree node
Binary tree nodes are defined as follows:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
Five basic forms of binary trees
Empty binary tree
There is only one root node
The root node has only the left subtree
The root node has only the right subtree
The root node has both left and right subtrees
There are only two situations for an ordinary tree with three nodes: two layers or three layers. But since the binary tree needs to distinguish left and right, it will evolve into the following five forms:
Special Binary Tree
Slanted Tree
As shown in the 2nd and 3rd pictures in the last picture above.
Full Binary Tree
In a binary tree, if all branch nodes have left subtrees and right subtrees, and all leaves are on the same level, such a binary tree is called a full binary tree. As shown below:
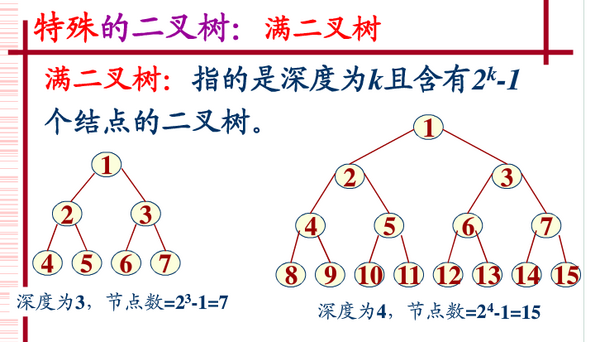
Complete Binary Tree
A complete binary tree means that the left side of the last level is full, the right side may be full or not, and then the remaining levels are full. A binary tree with depth k and number of nodes 2^k - 1 is a full binary tree (complete binary tree). It is a tree with depth k and no gaps.
The characteristics of a complete binary tree are:
Leaf nodes can only appear on the bottom two levels.
The lowest leaves must be concentrated on the left continuous position.
On the penultimate layer, if there are leaf nodes, they must be in continuous positions on the right.
If the node degree is 1, then the node has only left child.
A binary tree with the same node tree, a complete binary tree has the smallest depth.
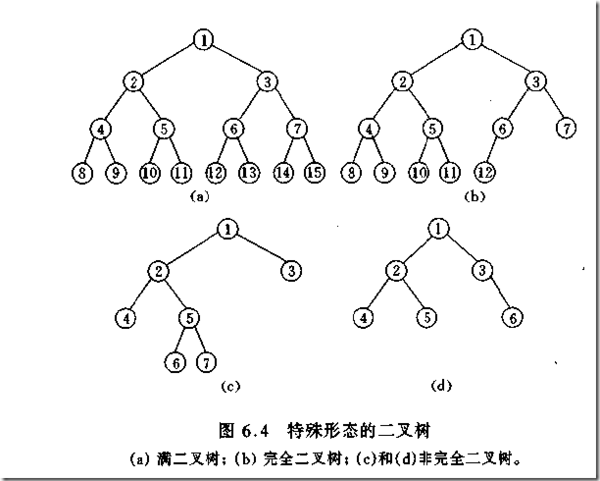
Note: A full binary tree must be a complete binary tree, but a complete binary tree is not necessarily a full binary tree.
The algorithm is as follows:
bool is_complete(tree *root)
{
queue q;
tree *ptr;
// Perform breadth-first traversal (level traversal) and put NULL nodes into the queue
q.push(root);
While ((ptr = q.pop()) != NULL)
{
q.push(ptr->left);
q.push(ptr->right);
}
// Determine whether there are any unvisited nodes
While (!q.is_empty())
{
ptr = q.pop();
// If there are unvisited non-NULL nodes, the tree has holes and is a non-complete binary tree
If (NULL != ptr)
return false;
}
return true;
}
Properties of binary trees
Property 1 of a binary tree: There are at most 2^(i-1) nodes (i>=1) on the i-th level of the binary tree
Property 2 of binary trees: A binary tree with depth k has at most 2^k-1 nodes (k>=1)
Sequential storage structure of binary tree
The sequential storage structure of a binary tree uses a one-dimensional array to store each node in the binary tree, and the storage location of the nodes can reflect the logical relationship between the nodes.
Binary linked list
Since the applicability of sequential storage is not strong, we must consider the chain storage structure. According to international practice, the storage of binary trees generally uses a chain storage structure.
Each node of a binary tree has at most two children, so it is a natural idea to design a data field and two pointer fields for it. We call such a linked list a binary linked list.
Binary tree traversal
Traversing a binary tree means starting from the root node and visiting all the nodes in the binary tree in a certain order so that each node is visited once and only once.
There are three ways to traverse a binary tree, as follows:
(1) Preorder traversal (DLR), first visit the root node, then traverse the left subtree, and finally traverse the right subtree. The abbreviation root-left-right.
(2) In-order traversal (LDR), first traverses the left subtree, then visits the root node, and finally traverses the right subtree. Abbreviated as left-root-right.
(3) Post-order traversal (LRD), first traverses the left subtree, then traverses the right subtree, and finally visits the root node. Abbreviated as left-right-root.
Preorder traversal:
If the binary tree is empty, no operation returns, otherwise the root node is visited first, then the left subtree is traversed in preorder, and then the right subtree is traversed in preorder.
The order of traversal is: A B D H I E J C F K G
//Pre-order traversal
function preOrder(node){
If(!node == null){
putstr(node.show() " ");
preOrder(node.left);
preOrder(node.right);
}
}
In-order traversal:
If the tree is empty, no operation returns, otherwise starting from the root node (note that the root node is not visited first), traverse the left subtree of the root node in in-order, then visit the root node, and finally Traverse the right subtree in order.
The order of traversal is: H D I B E J A F K C G
//Use recursion to implement in-order traversal
function inOrder(node){
If(!(node == null)){
inOrder(node.left);//Visit the left subtree first
putstr(node.show() " ");//Visit the root node again
inOrder(node.right);//Last access to the right subtree
}
}
Post-order traversal:
If the tree is empty, the no-op operation returns, otherwise the left and right subtrees are traversed from left to right, first the leaves and then the nodes, and finally the root node is visited.
The order of traversal is: H I D J E B K F G C A
//Post-order traversal
function postOrder(node){
If(!node == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
}
}
Implement binary search tree
Binary search tree (BST) is composed of nodes, so we define a Node node object as follows:
function Node(data,left,right){
This.data = data;
This.left = left;//Save the left node link
This.right = right;
This.show = show;
}
function show(){
Return this.data;//Display the data saved in the node
}
Find the maximum and minimum values
Finding the minimum and maximum values on a BST is very simple because the smaller value is always on the left child node. To find the minimum value on a BST, just traverse the left subtree until the last node is found
Find the minimum value
function getMin(){
var current = this.root;
While(!(current.left == null)){
Current = current.left;
}
Return current.data;
}
This method traverses the left subtree of the BST one by one until it traverses to the leftmost node of the BST, which is defined as:
current.left = null;
At this time, the value saved on the current node is the minimum value
Find the maximum value
Finding the maximum value on BST only requires traversing the right subtree until the last node is found, and the value saved on this node is the maximum value.
function getMax(){
var current = this.root;
While(!(current.right == null)){
current = current.right;
}
Return current.data;
}
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
