Programmer's Advanced Chapter: The Temperament of Hash Table
Mr. Zhang Yanpo joined Baishan Cloud Technology in 2016 and is mainly responsible for object storage research and development, data distribution across computer rooms, and repair and problem solving. With the goal of achieving 100PB-level data storage, he led the team to complete the design, implementation and deployment of a network-wide distributed storage system, separating "cold" and "hot" data, reducing the cost of cold data to 1.2 times the redundancy.
Mr. Zhang Yanpo worked for Sina from 2006 to 2015 and was responsible for the architecture design, collaboration process formulation, code specification and implementation standards formulation and most function implementation of Cross-IDC PB-level cloud storage service. Worked to support Sina's internal storage services such as Weibo, microdisk, video, SAE, music, software downloads, etc. From 2015 to 2016, he served as a senior technical expert at Meituan and designed a cross-machine room 100 PB object storage solution: Design and implement a high-concurrency and highly-reliable multi-copy replication strategy, and optimize erasure code to reduce 90% of IO overhead.
In software development, a hash table is equivalent to randomly placing n keys into b buckets to achieve storage of n data in b unit spaces.
We found some interesting phenomena in the hash table:
The distribution pattern of keys in the hash table
When the hash table When the number of keys and buckets is the same (n/b=1):
37% of the buckets are empty
37% of the buckets There is only 1 key in it
26% of the buckets have more than 1 key (hash conflict)
The following figure shows it intuitively When n=b=20, the number of keys in each bucket in the hash table (sort the buckets according to the number of keys):
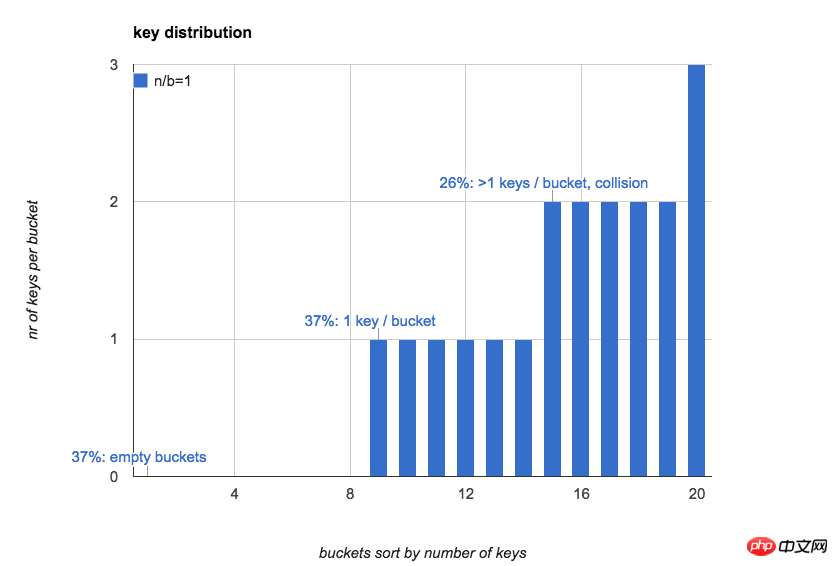
Often we use the hash table The first impression is: if keys are randomly put into all buckets, the number of keys in the bucket will be relatively uniform, and the expected number of keys in each bucket is 1.
In fact, the distribution of keys in the bucket is very uneven when n is small; when n increases, it will gradually become even.
The impact of the number of keys on the number of buckets in category 3
The following table shows how the value of n/b affects category 3 when b remains unchanged and n increases. The proportion of the number of buckets (the conflict rate is the proportion of buckets containing more than 1 key):
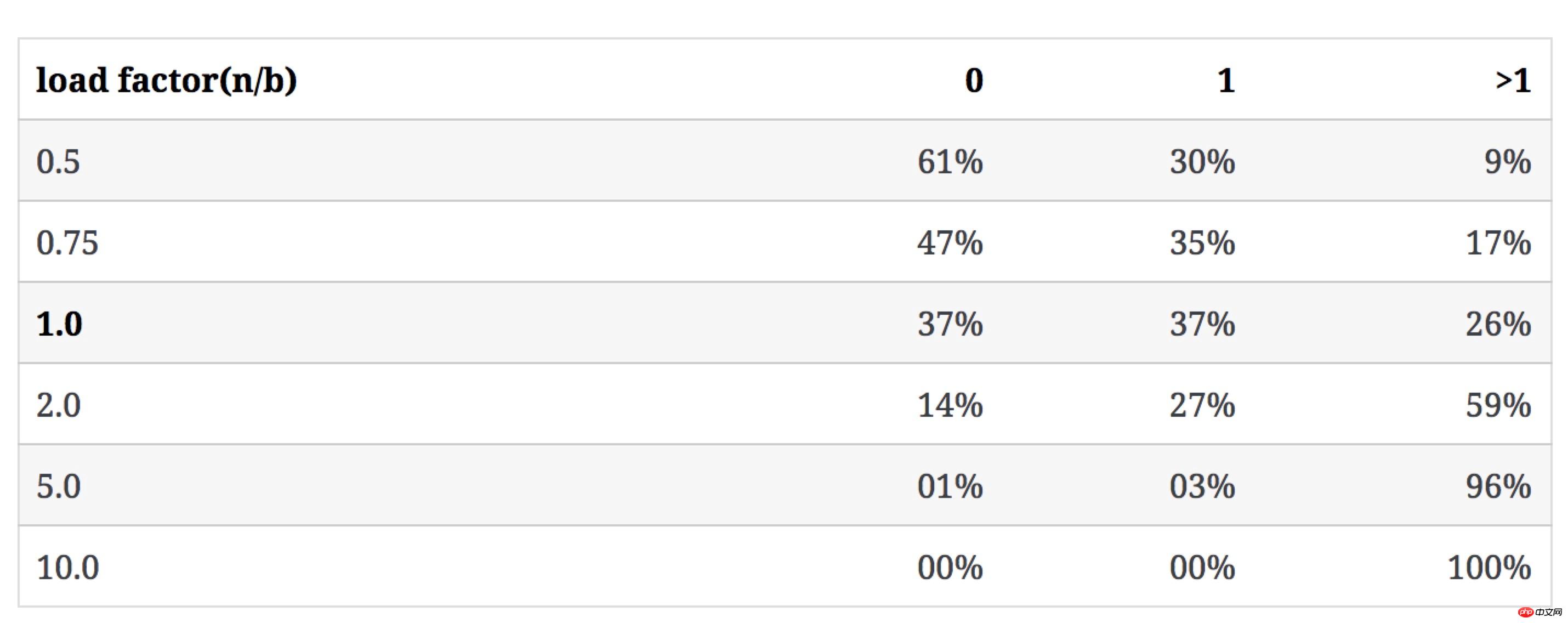
To be more intuitive, we use the following figure to show the empty bucket rate and The changing trend of conflict rate with n/b value:
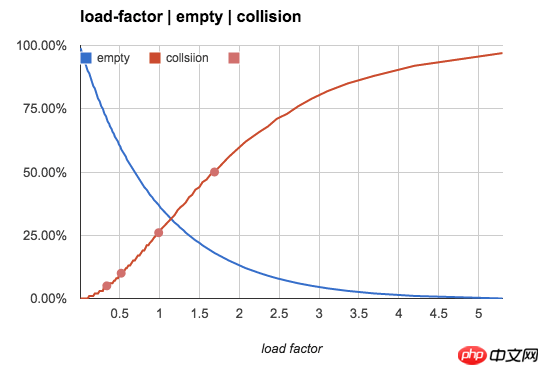
The impact of the number of keys on the uniformity of the bucket
The above sets of numbers It is a meaningful reference value when n/b is small, but as n/b gradually increases, the number of empty buckets and buckets with one key is almost 0, and most buckets contain multiple keys.
When n/b exceeds 1 (one bucket allows multiple keys to be stored), our main observation object becomes the distribution pattern of the number of keys in the bucket.
The following table shows the degree of unevenness when n/b is large and the number of keys in each bucket tends to be uniform.
In order to describe the degree of unevenness, we use the ratio between the maximum and minimum number of keys in the bucket ((most-fewest)/most) to express it.
The following table lists the distribution of keys as n increases when b=100.
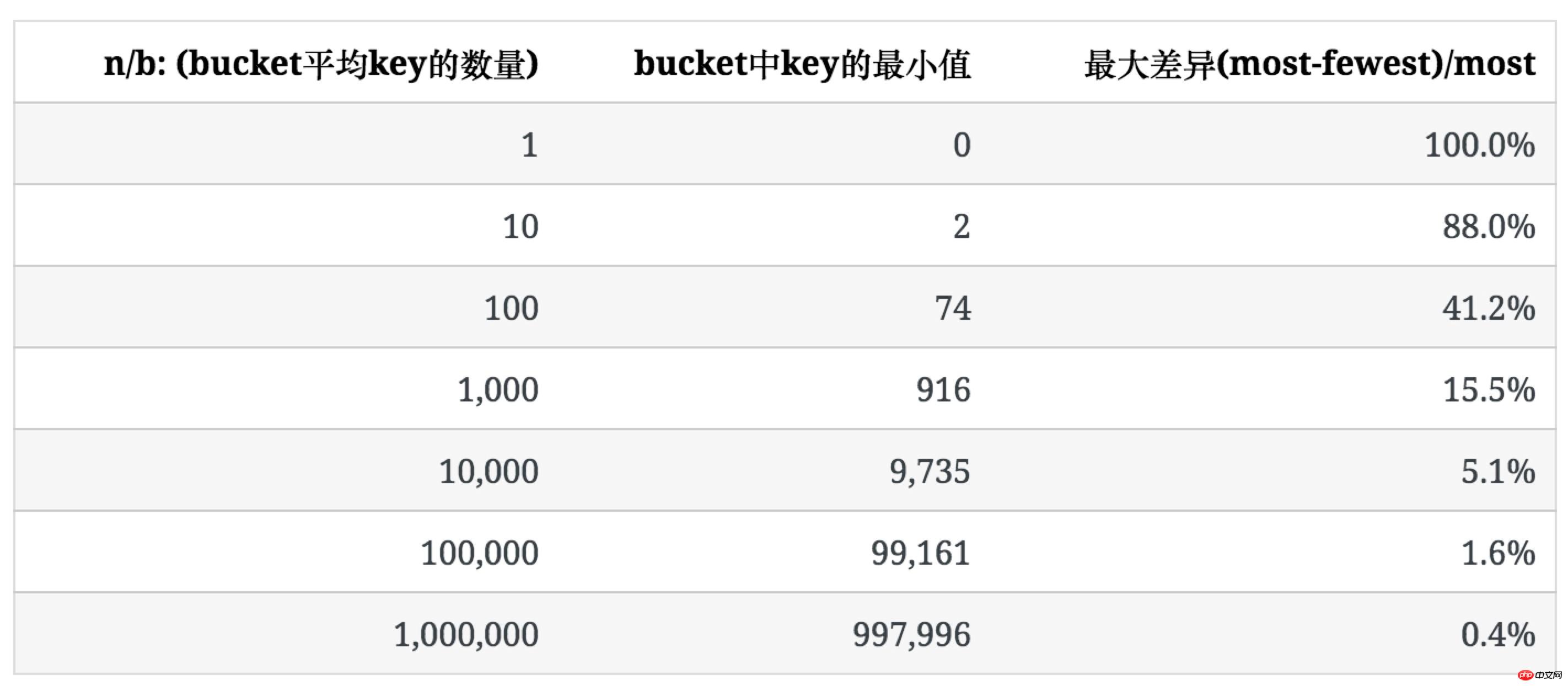
It can be seen that as the average number of keys in the bucket increases, the unevenness of its distribution gradually decreases.
和空bucket或1个key的bucket的占比不同n/b,均匀程度不仅取决于n/b的值,也受b值的影响,后面会提到。 未使用统计中常用的均方差法去描述key分布的不均匀程度,是因为软件开发过程中,更多时候要考虑最坏情况下所需准备的内存等资源。
Load Factor: n/b
A concept commonly used in hash tables, load factor α=n/b, is used to describe the characteristics of hash tables.
Usually, based on memory storage hash table, its n/b ≤0.75. This setting can not only save space, but also keep the key conflict rate relatively low. A low conflict rate means low frequency hash relocation, and the insertion of the hash table will be faster.
线性探测是一个经常被使用的解决插入时hash冲突的算法,它在1个bucket出现冲突时,按照逐步增加的步长顺序向后查看这个bucket后面的bucket,直到找到1个空bucket。因此它对hash的冲突非常敏感。
In this scenario of n/b=0.75, if linear detection is not used (such as using a linked list in the bucket to save multiple keys), about 47% of the buckets are empty; if linear detection is used , among these 47% buckets, about half of the buckets will be filled by linear detection.
在很多内存hash表的实现中,选择n/b=<p><strong>Hash table feature tips: </strong></p>
The hash table itself is an algorithm that exchanges a certain amount of space for efficiency. Low time overhead (O(1)), low space waste, and low conflict rate cannot be achieved at the same time;
hash tables are only suitable for the storage of pure memory data structures:
The hash table exchanges space for an increase in access speed; the waste of disk space is intolerable, but a small waste of memory is acceptable;
Hash tables are only suitable for storage media with fast random access. Data storage on the hard disk mostly uses btrees or other ordered data structures.
Most high-level languages (built-in hash table, hash set, etc.) maintain n/b≤
The hash table will not distribute keys evenly when n/b is small.
Load Factor:n/b>1
另外一种hash表的实现,专门用来存储比较多的key,当 n/b>1n/b1.0时,线性探测失效(没有足够的bucket存储每个key)。这时1个bucket里不仅存储1个key,一般在一个bucket内用chaining,将所有落在这个bucket的key用链表连接起来,来解决冲突时多个key的存储。
链表只在n/b不是很大时适用。因为链表的查找需要O(n)的时间开销,对于非常大的n/b,有时会用tree替代链表来管理bucket内的key。
n/b值较大的使用场景之一是:将一个网站的用户随机分配到多个不同的web-server上,这时每个web-server可以服务多个用户。多数情况下,我们都希望这种分配能尽可能均匀,从而有效利用每个web-server资源。
这就要求我们关注hash的均匀程度。因此,接下来要讨论的是,假定hash函数完全随机的,均匀程度根据n和b如何变化。
n/b 越大,key的分布越均匀
当 n/b 足够大时,空bucket率趋近于0,且每个bucket中key的数量趋于平均。每个bucket中key数量的期望是:
avg=n/b
定义一个bucket平均key的数量是100%:bucket中key的数量刚好是n/b,下图分别模拟了 b=20,n/b分别为 10、100、1000时,bucket中key的数量分布。
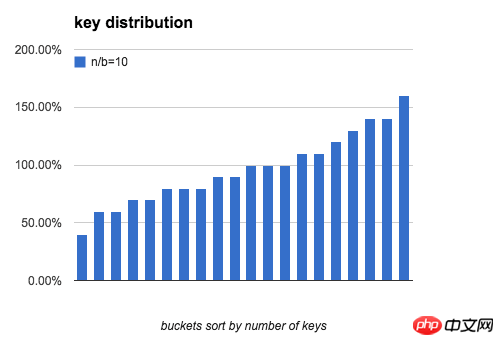
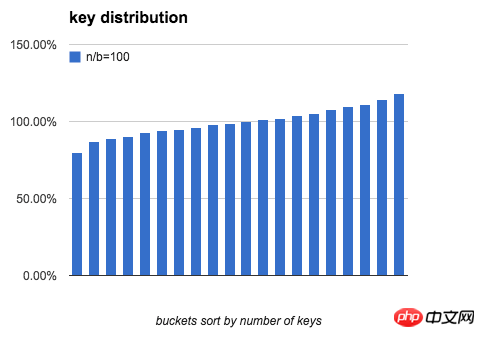
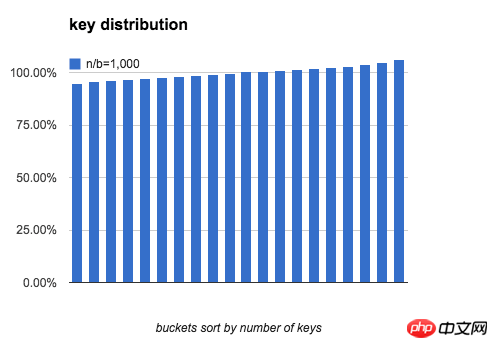
可以看出,当 n/b 增大时,bucket中key数量的最大值与最小值差距在逐渐缩小。下表列出了随b和n/b增大,key分布的均匀程度的变化:
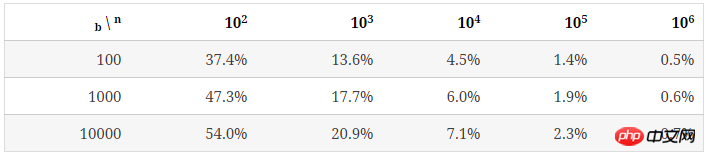
结论:
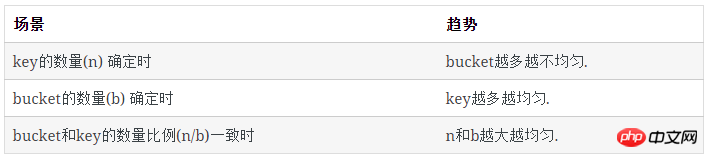
计算
上述大部分结果来自于程序模拟,现在我们来解决从数学上如何计算这些数值。
每类bucket的数量
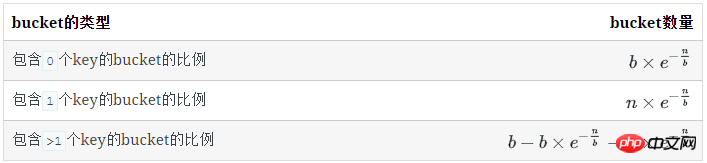
空bucket数量
对于1个key, 它不在某个特定的bucket的概率是 (b−1)/b
所有key都不在某个特定的bucket的概率是( (b−1)/b)n
已知:
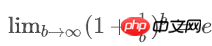
空bucket率是:
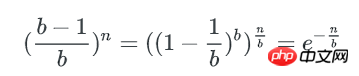
空bucket数量为:

有1个key的bucket数量
n个key中,每个key有1/b的概率落到某个特定的bucket里,其他key以1-(1/b)的概率不落在这个bucket里,因此,对某个特定的bucket,刚好有1个key的概率是:
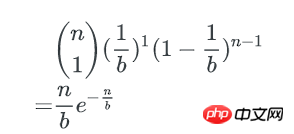
刚好有1个key的bucket数量为:
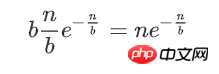
多个key的bucket
剩下即为含多个key的bucket数量:
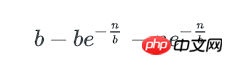
key在bucket中分布的均匀程度
类似的,1个bucket中刚好有i个key的概率是:n个key中任选i个,并都以1/b的概率落在这个bucket里,其他n-i个key都以1-1/b的概率不落在这个bucket里,即:
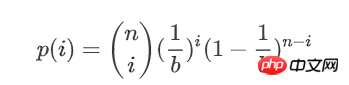
这就是著名的二项式分布。
我们可通过二项式分布估计bucket中key数量的最大值与最小值。
通过正态分布来近似
当 n, b 都很大时,二项式分布可以用正态分布来近似估计key分布的均匀性:
p=1/b,1个bucket中刚好有i个key的概率为:
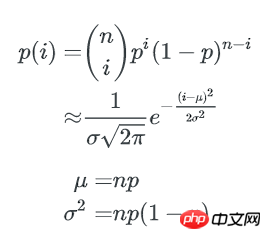
1个bucket中key数量不多于x的概率是:
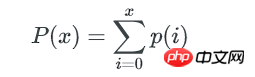
所以,所有不多于x个key的bucket数量是:
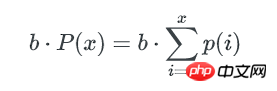
bucket中key数量的最小值,可以这样估算: 如果不多于x个key的bucket数量是1,那么这唯一1个bucket就是最少key的bucket。我们只要找到1个最小的x,让包含不多于x个key的bucket总数为1, 这个x就是bucket中key数量的最小值。
计算key数量的最小值x
一个bucket里包含不多于x个key的概率是:
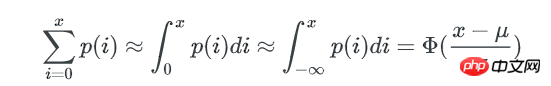
Φ(x) 是正态分布的累计分布函数,当x-μ趋近于0时,可以使用以下方式来近似:
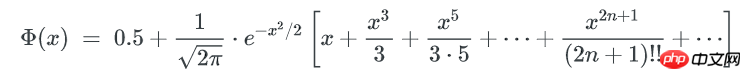
这个函数的计算较难,但只是要找到x,我们可以在[0~μ]的范围内逆向遍历x,以找到一个x 使得包含不多于x个key的bucket期望数量是1。
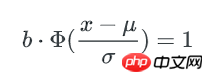
x可以认为这个x就是bucket里key数量的最小值,而这个hash表中,不均匀的程度可以用key数量最大值与最小值的差异来描述: 因为正态分布是对称的,所以key数量的最大值可以用 μ + (μ-x) 来表示。最终,bucket中key数量最大值与最小值的比例就是:
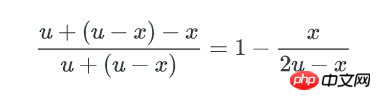
(μ是均值n/b)
程序模拟
以下python脚本模拟了key在bucket中分布的情况,同时可以作为对比,验证上述计算结果。
import sysimport mathimport timeimport hashlibdef normal_pdf(x, mu, sigma):
x = float(x)
mu = float(mu)
m = 1.0 / math.sqrt( 2 * math.pi ) / sigma
n = math.exp(-(x-mu)**2 / (2*sigma*sigma))return m * ndef normal_cdf(x, mu, sigma):
# integral(-oo,x)
x = float(x)
mu = float(mu)
sigma = float(sigma) # to standard form
x = (x - mu) / sigma
s = x
v = x for i in range(1, 100):
v = v * x * x / (2*i+1)
s += v return 0.5 + s/(2*math.pi)**0.5 * math.e ** (-x*x/2)def difference(nbucket, nkey):
nbucket, nkey= int(nbucket), int(nkey) # binomial distribution approximation by normal distribution
# find the bucket with minimal keys.
#
# the probability that a bucket has exactly i keys is:
# # probability density function
# normal_pdf(i, mu, sigma)
#
# the probability that a bucket has 0 ~ i keys is:
# # cumulative distribution function
# normal_cdf(i, mu, sigma)
#
# if the probability that a bucket has 0 ~ i keys is greater than 1/nbucket, we
# say there will be a bucket in hash table has:
# (i_0*p_0 + i_1*p_1 + ...)/(p_0 + p_1 + ..) keys.
p = 1.0 / nbucket
mu = nkey * p
sigma = math.sqrt(nkey * p * (1-p))
target = 1.0 / nbucket
minimal = mu while True:
xx = normal_cdf(minimal, mu, sigma) if abs(xx-target) < target/10: break
minimal -= 1
return minimal, (mu-minimal) * 2 / (mu + (mu - minimal))def difference_simulation(nbucket, nkey):
t = str(time.time())
nbucket, nkey= int(nbucket), int(nkey)
buckets = [0] * nbucket for i in range(nkey):
hsh = hashlib.sha1(t + str(i)).digest()
buckets[hash(hsh) % nbucket] += 1
buckets.sort()
nmin, mmax = buckets[0], buckets[-1] return nmin, float(mmax - nmin) / mmaxif __name__ == "__main__":
nbucket, nkey= sys.argv[1:]
minimal, rate = difference(nbucket, nkey) print 'by normal distribution:'
print ' min_bucket:', minimal print ' difference:', rate
minimal, rate = difference_simulation(nbucket, nkey) print 'by simulation:'
print ' min_bucket:', minimal print ' difference:', rateThe above is the detailed content of Programmer's Advanced Chapter: The Temperament of Hash Table. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1666
1666
 14
14
 1425
1425
 52
52
 1325
1325
 25
25
 1272
1272
 29
29
 1252
1252
 24
24
 Which AI programmer is the best? Explore the potential of Devin, Tongyi Lingma and SWE-agent
Apr 07, 2024 am 09:10 AM
Which AI programmer is the best? Explore the potential of Devin, Tongyi Lingma and SWE-agent
Apr 07, 2024 am 09:10 AM
On March 3, 2022, less than a month after the birth of the world's first AI programmer Devin, the NLP team of Princeton University developed an open source AI programmer SWE-agent. It leverages the GPT-4 model to automatically resolve issues in GitHub repositories. SWE-agent's performance on the SWE-bench test set is similar to Devin, taking an average of 93 seconds and solving 12.29% of the problems. By interacting with a dedicated terminal, SWE-agent can open and search file contents, use automatic syntax checking, edit specific lines, and write and execute tests. (Note: The above content is a slight adjustment of the original content, but the key information in the original text is retained and does not exceed the specified word limit.) SWE-A
 520 programmers' exclusive way to express romantic feelings! Can't refuse!
May 19, 2022 pm 03:07 PM
520 programmers' exclusive way to express romantic feelings! Can't refuse!
May 19, 2022 pm 03:07 PM
520 is approaching, and he is here again for the annual show of tormenting dogs! Want to see how the most rational code and the most romantic confession can collide? Let’s take you through the most complete and complete advertising code one by one to see if the romance of programmers can capture the hearts of your goddesses?
 Revealing the appeal of C language: Uncovering the potential of programmers
Feb 24, 2024 pm 11:21 PM
Revealing the appeal of C language: Uncovering the potential of programmers
Feb 24, 2024 pm 11:21 PM
The Charm of Learning C Language: Unlocking the Potential of Programmers With the continuous development of technology, computer programming has become a field that has attracted much attention. Among many programming languages, C language has always been loved by programmers. Its simplicity, efficiency and wide application make learning C language the first step for many people to enter the field of programming. This article will discuss the charm of learning C language and how to unlock the potential of programmers by learning C language. First of all, the charm of learning C language lies in its simplicity. Compared with other programming languages, C language
 Make money by taking on private jobs! A complete list of order-taking platforms for programmers in 2023!
Jan 09, 2023 am 09:50 AM
Make money by taking on private jobs! A complete list of order-taking platforms for programmers in 2023!
Jan 09, 2023 am 09:50 AM
Last week we did a public welfare live broadcast about "2023PHP Entrepreneurship". Many students asked about specific order-taking platforms. Below, php Chinese website has compiled 22 relatively reliable platforms for reference!
 2023过年,又限制放烟花?程序猿有办法!
Jan 20, 2023 pm 02:57 PM
2023过年,又限制放烟花?程序猿有办法!
Jan 20, 2023 pm 02:57 PM
本篇文章给大家介绍如何用前端代码实现一个烟花绽放的绚烂效果,其实主要就是用前端三剑客来实现,也就是HTML+CSS+JS,下面一起来看一下,作者会解说相应的代码,希望对需要的朋友有所帮助。
 what do programmers do
Aug 03, 2019 pm 01:40 PM
what do programmers do
Aug 03, 2019 pm 01:40 PM
Programmer's job responsibilities: 1. Responsible for the detailed design, coding and organization and implementation of internal testing of software projects; 2. Assist project managers and related personnel to communicate with customers and maintain good customer relationships; 3. Participate in demand research and project feasibility performance analysis, technical feasibility analysis and demand analysis; 4. Familiar with and proficient in the relevant software technologies for delivering software projects developed by the software department; 5. Responsible for timely feedback on software development situations to the project manager; 6. Participate in software development and maintenance Solve major technical problems during the process; 7. Responsible for the formulation of relevant technical documents, etc.
 How to implement Redis Hash operation in php
May 30, 2023 am 08:58 AM
How to implement Redis Hash operation in php
May 30, 2023 am 08:58 AM
Hash operation //Assign values to fields in the hash table. Returns 1 on success and 0 on failure. If the hash table does not exist, the table will be created first and then the value will be assigned. If the field already exists, the old value will be overwritten. $ret=$redis->hSet('user','realname','jetwu');//Get the value of the specified field in the hash table. If the hash table does not exist, return false. $ret=$redis->hGet('user','rea
 A brief analysis of how to download and install historical versions of VSCode
Apr 17, 2023 pm 07:18 PM
A brief analysis of how to download and install historical versions of VSCode
Apr 17, 2023 pm 07:18 PM
Download and install historical versions of VSCode VSCode installation download installation reference VSCode installation Windows version: Windows10 VSCode version: VScode1.65.0 (64-bit User version) This article




