
This article mainly introducesPythonProgrammingimplementation of binary trees and seven traversal methods. It analyzes in detail the definition of Python binary trees and common traversal operation techniques in the form of examples. Friends in need You can refer to the following
The examples in this article describe the implementation of binary trees and traversal methods in Python. Share it with everyone for your reference, the details are as follows:
Introduction:
Tree is a very important type of data structure, its main purpose It is used to improve search efficiency, and is more effective when repeated searches are required, such as binary sorting trees and FP-trees. In addition, it can be used to improve coding efficiency, such as Huffman tree.
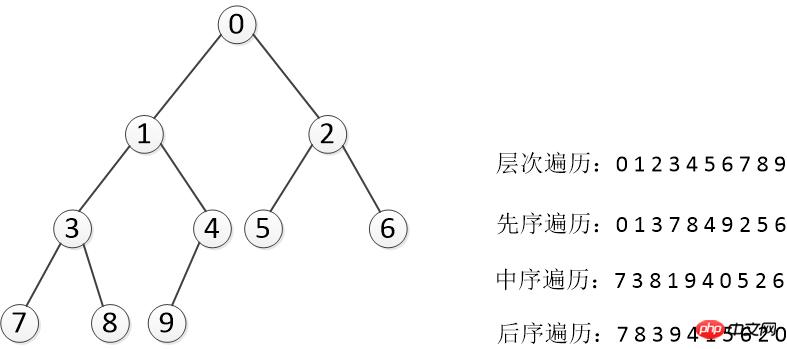
Code:
Use Python to implement tree construction and several traversal algorithms, although it is not difficult , but I still organized and summarized the code. Implementation functions:
① Tree construction
② Recursion Implement pre-order traversal, mid-order traversal, and post-order traversal
③ Stack implements pre-order traversal, mid-order traversal, Post-order traversal
④ QueueImplementing hierarchical traversal
#coding=utf-8
class Node(object):
"""节点类"""
def init(self, elem=-1, lchild=None, rchild=None):
self.elem = elem
self.lchild = lchild
self.rchild = rchild
class Tree(object):
"""树类"""
def init(self):
self.root = Node()
self.myQueue = []
def add(self, elem):
"""为树添加节点"""
node = Node(elem)
if self.root.elem == -1: # 如果树是空的,则对根节点赋值
self.root = node
self.myQueue.append(self.root)
else:
treeNode = self.myQueue[0] # 此结点的子树还没有齐。
if treeNode.lchild == None:
treeNode.lchild = node
self.myQueue.append(treeNode.lchild)
else:
treeNode.rchild = node
self.myQueue.append(treeNode.rchild)
self.myQueue.pop(0) # 如果该结点存在右子树,将此结点丢弃。
def front_digui(self, root):
"""利用递归实现树的先序遍历"""
if root == None:
return
print root.elem,
self.front_digui(root.lchild)
self.front_digui(root.rchild)
def middle_digui(self, root):
"""利用递归实现树的中序遍历"""
if root == None:
return
self.middle_digui(root.lchild)
print root.elem,
self.middle_digui(root.rchild)
def later_digui(self, root):
"""利用递归实现树的后序遍历"""
if root == None:
return
self.later_digui(root.lchild)
self.later_digui(root.rchild)
print root.elem,
def front_stack(self, root):
"""利用堆栈实现树的先序遍历"""
if root == None:
return
myStack = []
node = root
while node or myStack:
while node: #从根节点开始,一直找它的左子树
print node.elem,
myStack.append(node)
node = node.lchild
node = myStack.pop() #while结束表示当前节点node为空,即前一个节点没有左子树了
node = node.rchild #开始查看它的右子树
def middle_stack(self, root):
"""利用堆栈实现树的中序遍历"""
if root == None:
return
myStack = []
node = root
while node or myStack:
while node: #从根节点开始,一直找它的左子树
myStack.append(node)
node = node.lchild
node = myStack.pop() #while结束表示当前节点node为空,即前一个节点没有左子树了
print node.elem,
node = node.rchild #开始查看它的右子树
def later_stack(self, root):
"""利用堆栈实现树的后序遍历"""
if root == None:
return
myStack1 = []
myStack2 = []
node = root
myStack1.append(node)
while myStack1: #这个while循环的功能是找出后序遍历的逆序,存在myStack2里面
node = myStack1.pop()
if node.lchild:
myStack1.append(node.lchild)
if node.rchild:
myStack1.append(node.rchild)
myStack2.append(node)
while myStack2: #将myStack2中的元素出栈,即为后序遍历次序
print myStack2.pop().elem,
def level_queue(self, root):
"""利用队列实现树的层次遍历"""
if root == None:
return
myQueue = []
node = root
myQueue.append(node)
while myQueue:
node = myQueue.pop(0)
print node.elem,
if node.lchild != None:
myQueue.append(node.lchild)
if node.rchild != None:
myQueue.append(node.rchild)
if name == 'main':
"""主函数"""
elems = range(10) #生成十个数据作为树节点
tree = Tree() #新建一个树对象
for elem in elems:
tree.add(elem) #逐个添加树的节点
print '队列实现层次遍历:'
tree.level_queue(tree.root)
print '\n\n递归实现先序遍历:'
tree.front_digui(tree.root)
print '\n递归实现中序遍历:'
tree.middle_digui(tree.root)
print '\n递归实现后序遍历:'
tree.later_digui(tree.root)
print '\n\n堆栈实现先序遍历:'
tree.front_stack(tree.root)
print '\n堆栈实现中序遍历:'
tree.middle_stack(tree.root)
print '\n堆栈实现后序遍历:'
tree.later_stack(tree.root)Summary:
There are two main types of tree traversal One is depth-first traversal, like preorder, midorder, and postorder; the other is breadth-first traversal, like hierarchical traversal. The difference between the two is not very obvious in the tree structure, but when extending from a tree to a directed graph to an undirected graph, the efficiency and effect of depth-first search and breadth-first search are still very great. different.
Depth first generally uses recursion, and breadth first generally uses queues. In general, most algorithms that can be implemented using recursion can also be implemented using stacks. I have the impression that there is a way to construct a tree recursively, but I have never been able to figure out how to construct it. After thinking about it carefully,The above is the detailed content of Detailed explanation of how to implement binary trees and seven traversal methods in Python programming. For more information, please follow other related articles on the PHP Chinese website!




