基于马尔科夫边界发现的因果特征选择算法综述

摘要

因果特征选择算法(也称为马尔科夫边界发现)学习目标变量的马尔科夫边界,选择与目标存在因果关系的特征,具有比传统方法更好的可解释性和鲁棒性.文中对现有因果特征选择算法进行全面综述,分为单重马尔科夫边界发现算法和多重马尔科夫边界发现算法.基于每类算法的发展历程,详细介绍每类的经典算法和研究进展,对比它们在准确性、效率、数据依赖性等方面的优劣.此外,进一步总结因果特征选择在特殊数据(半监督数据、多标签数据、多源数据、流数据等)中的改进和应用.最后,分析该领域的当前研究热点和未来发展趋势,并建立因果特征选择资料库(http://home.ustc.edu.cn/~xingyuwu/MB.html),汇总该领域常用的算法包和数据集.

    高维数据为真实世界的机器学习任务带来诸多挑战, 如计算资源和存储资源的消耗、数据的过拟合, 学习算法的性能退化[1], 而最具判别性的信息仅被一部分相关特征携带[2].为了降低数据维度, 避免维度灾难, 特征选择研究受到广泛关注.大量的实证研究[3, 4, 5]表明, 对于多数涉及数据拟合或统计分类的机器学习算法, 在去除不相关特征和冗余特征的特征子集上, 通常能获得比在原始特征集合上更好的拟合度或分类精度.此外, 选择更小的特征子集有助于更好地理解底层的数据生成流程[6].

　　传统的特征选择算法主要分为封装法、过滤法和嵌入法三类[7].封装法[8]为不同的特征子集训练一个学习器, 评估其在该特征子集上的表现, 决定所选特征子集.过滤法[9]使用一个评估函数, 为特征评分并选择分数较高的特征, 因此不依赖额外的分类器, 更高效.嵌入法[10]将特征选择过程嵌入学习过程中, 同时搜索特征选择空间和学习器参数空间, 获得特征子集.

　　传统的特征选择算法根据特征和目标变量之间的相关性寻找相关特征子集[11].然而, 相关关系只能反映目标变量和特征之间的共存关系, 而无法解释决定目标变量取值的潜在机制[12, 13].一些研究表明[12, 13], 因果关系具有更好的可解释性和鲁棒性.例如, 将吸烟与肺ai患者数据集上“ 肺ai” (例子中变量取值均为“ 是” 、“ 否” )作为目标变量, “ 黄手指” 和“ 吸烟” 作为特征变量.由于“ 吸烟” 可用来解释“ 肺ai” , 而长期吸烟手指会受到焦油的污染, 因此“ 黄手指” 和“ 吸烟” 与“ 肺ai” 之间存在相关关系, 而只有“ 吸烟” 与“ 肺ai” 之间存在因果关系.当一些吸烟者为了隐藏吸烟习惯而去除手指上的黄渍时, 基于“ 黄手指” 的yuce模型将失效, 而基于“ 吸烟” 的yuce模型更鲁棒.

　　为了寻找更鲁棒的因果特征, 近年来, 因果特征选择算法被广泛研究.该类算法通过学习目标变量的马尔科夫边界(Markov Boundary, MB)[14]以寻找关键特征, 因此又被称为MB发现算法.具体地, MB的概念来源于因果贝叶斯网络, 在满足忠实性假设的贝叶斯网络中, 一个变量的MB集合是唯一的, 包含该目标变量的父节点、子节点及配偶节点(子节点的其它父节点)[14].因此, MB反映目标变量周围的局部因果关系, 给定目标变量的MB作为条件集合, 其它特征条件独立于目标变量[14].基于此属性:Tsamardinos等[15]证明在分类问题中, 类别变量的MB是具有最大yuce性的最小特征子集; Pellet等[16]证明类别变量的MB集合是特征选择的最优解.因此, 因果特征选择算法通常具有可靠的理论保证.

作为一种算法思路, 基于因果关系的特征选择算法促进特征选择的可解释性和鲁棒性.近年来, 因果特征选择算法不断发展, 不仅提升单/多重马尔科夫边界发现算法的搜索精度和计算效率, 在半监督数据、流数据、多源数据、多标签数据等特殊场景下也不断发展.这些算法无需学习包含所有特征的完整贝叶斯网络结构, 即可挖掘目标变量周围的因果特征.本文对现有因果特征选择方法进行较全面的研究和综述.

基于原理与现有方法分类

1.问题定义与基础理论

本节介绍MB相关的基本定义和基础理论.本文使用U表示特征集合, T表示目标变量(标签).MB的概念来源于人工智能基础模型之一的贝叶斯网络.

定义 1 贝叶斯网络[14] 对于三元组< U, G, P> , U表示变量集合, G表示U上的有向无环图(Directed Acyclic Graph, DAG), P表示U上的概率分布.对于∀ X∈ U, 将X在G中的父变量作为条件集合, 如果任意X的非后代变量在P中都条件独立于X, 那么< U, G, P> 为贝叶斯网络.

贝叶斯网络表征一个变量集合中的因果关系.在有向无环图中, 对于一对直接相连的父子变量, 父变量是子变量的直接原因, 子变量是父变量的直接结果[14].忠实性是贝叶斯网络的基础假设之一, 定义如下.

定义 2 忠实性[14] 给定贝叶斯网络< U, G, P> , G忠实于P当且仅当P中的每个条件独立性关系都是由G和马尔科夫条件决定的.P忠实于G当且仅当存在一个G的子图忠实于P.

MB的概念是基于忠实的贝叶斯网络而提出的, 定义如下.

定义 3 马尔科夫边界[14] 在满足忠实性的贝叶斯网络中, 一个节点的马尔科夫边界包含该节点的父节点、子节点和配偶节点(子节点的其它父节点)[14].

根据定义3, 一个节点的MB可直接从忠实的贝叶斯网络中“ 读” 出来.如图1所示, 节点T的MB为{A, B, G, H, F}, 包含父节点A、B, 子节点G、H, 配偶节点F.从因果图的角度分析, MB提供变量周围的局部因果结构, 父节点、子节点、配偶节点分别对应目标变量的直接原因、直接结果、直接结果的其它原因.MB发现算法通过挖掘变量的局部因果结构, 无需学习完整的贝叶斯网络即可找到变量的MB.而变量的MB集合有一个特殊的统计特性, 见定理1.

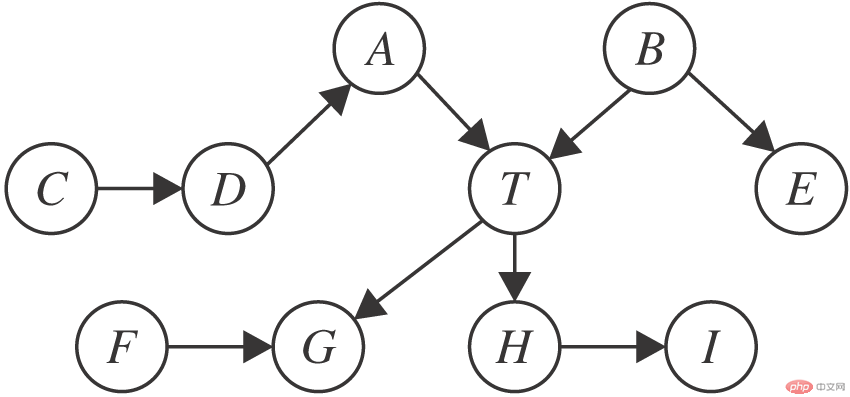
图1 马尔科夫边界的例子

Fig.1 An example of Markov boundary

定理 1 对于变量X∈ U, X的马尔科夫边界MB⊆U, 满足:∀ Y∈ U-MB-{X}, X⊥Y| MB, 且MB为满足该统计特性的最小变量集.

定理1 中阐述MB的最小性, MB的超集通常称为马尔科夫毯(Markov Blanket).根据定理1, 以MB集合为条件, 目标变量会条件独立于其它特征.因此, MB中的特征携带所有关于目标变量的yuce信息, 并且其“ 最小性” 保证MB可作为特征选择问题的最优解, 见定理2.

定理 2 在满足忠实性假设的数据中, 目标变量的MB是唯一的, 并且为特征选择的最优解[15, 16].

定理2 为MB发现算法解决特征选择问题提供理论保证, 由于MB发现算法根据数据中的因果关系选择特征, 并且特征包含目标变量的因果信息, 因此使用MB发现算法选择特征的过程称为因果特征选择.

2.现有马尔科夫边界学习方法分类及其基本原理

图2给出本文对现有MB发现算法的分类.常规数据中的MB发现算法主要分为单重MB发现算法和多重MB发现算法, 这两类算法的应用场景取决于训练数据是否满足忠实性假设.根据定理2, 在满足忠实性的条件下, 目标变量的MB是唯一的, 当真实数据并不完全满足忠实性条件时, 目标变量可能存在多个等价的MB.因此, 一部分现有算法假设数据满足忠实性, 并且试图寻找目标变量的唯一MB, 该类算法称为单重MB发现算法.另一部分算法考虑忠实性假设被违反的情况, 这些算法可挖掘目标变量的多个等价MB, 该类算法称为多重MB发现算法.特殊数据中的MB发现算法作为一类单独介绍, 其中包括半监督数据MB发现算法、流数据MB发现算法、多源数据MB发现算法、多标签数据MB发现算法.本文按照上述分类介绍现有算法的特点.  

图2 现有MB发现算法的分类

Fig.2 Categories of existing MB discovery algorithms

单重MB发现算法假设目标变量有唯一的MB, 输出的MB集合可直接作为特征选择的结果.该类算法主要分为两类:直接的MB发现算法(直接法)和分治的MB发现算法(分治法).主要区别是:直接法根据MB的性质(定理1)直接学习MB变量, 而分治法分别学习父子变量和配偶变量.主要理论依据为定理3和定理4.

定理 3 在U上的贝叶斯网络中, 如果节点X和Y满足:任意变量子集Z⊆U-{X, Y}, X⊥Y|Z不成立, 那么X和Y是一对父子变量[17].

定理 4 在U上的贝叶斯网络中, 如果不相连的节点X和Y均与T相连, 如果存在变量子集Z⊆U-{X, Y, T}, 使得X⊥Y|Z成立但X⊥Y|Z∪ {T}不成立, 那么X和Y是一对配偶变量[17].

定理3和定理4分别给出父子变量和配偶变量的判别条件, 基于上述定理, 分治的MB发现算法可通过条件独立性测试分别搜索父子和配偶变量.

如图3所示, 单重MB发现算法通常使用增长阶段和收缩阶段搜索MB变量或父子变量.增长阶段用于识别并添加可能的真变量, 而收缩阶段检测并删除增长步骤中找到的假变量.基于这一框架, 分治法需要进一步搜索配偶变量.直接法通常在时间效率上更优.但由于分治法在条件独立性测试中使用规模更小的条件集合, 因此通常分治法可达到比直接法更高的准确性.

图3 直接法和分治法的区别

Fig.3 Difference between direct methods and divide-and-conquer methods

    可用于MB发现算法的通用条件独立性测试方法有5种:1)λ 2测试、G2测试、互信息计算, 可用于离散数据[18]; 2)菲尔逊Z检验[19], 可用于带有高斯误差的线性关系的连续数据; 3)基于核的条件独立性测试方法[20], 可用于非线性、非高斯噪声的连续数据.

多重MB发现算法研究忠实性假设被违反的情况下一个变量的多个等价MB.理论上来说, 目标变量的多重MB携带等价的信息且具有相似的yuce能力[21], 该类算法存在的意义是:1)由于实际应用中多个等价的MB适应的特定学习模型是不同的, 多重MB可用于解释学习模型的多样性现象; 2)实际应用中可能存在多个等价的MB, 但并非所有MB都适合作为特征子集建立学习模型.例如, 当不同变量的获取成本可能不同时, 多重MB算法可用于探索较低获取成本但具有相似yuce性的替代解决方案(特征子集).

根据Statnikov等[21]的研究, 多重MB的本质原因是等价信息现象, 定义4和定理5如下.

定义 4 等价信息[21] 对变量集合X⊆U, Y⊆U及目标变量T∈ U, X和Y包含T的等价信息当且仅当X和Y与T相关且满足X⊥T|Y, Y⊥T|X.

定理 5 当且仅当没有发生信息等价时, 目标变量有一个唯一的MB集合[21].

根据定理5, 多重MB与等价信息现象是共存的, 因此寻找多个MB的过程也就是识别等价信息的过程[21].现有的多重MB发现算法通常遵循如下步骤:1)使用单重MB发现算法找到一个初始的MB; 2)在当前MB中选择特征子集, 将其从源数据分布中移除, 再在新的数据分布中找到新的MB; 3)测试新MB是否正确.

特殊数据的MB发现算法主要是面向近年来逐渐流行的一些特殊学习场景, 根据本文的调研, 目前主要包括但不限于:半监督数据MB发现算法、多标签数据MB发现算法、多源数据MB发现算法和流数据MB发现算法.这些算法大多对应某个单重MB发现算法, 考虑对应场景的特点, 将单重MB算法扩展应用到特殊数据中.