Thinkphp的list_to_tree 实现无限级分类列出所有节点
Thinkphp的list_to_tree 实现无限级分类列出所有节点
list_to_tree 使用起来十分方便,详细可查看手册。因为我在用的时候需要同时列出所有节点,所以写了一个递归函数,拿出来供大家参考。public function index(){
Load('extend'); //加载扩展方法
$Category=D('Category');
$list=$Category->order('sort desc')->select();//实现同级节点排序
$list=list_to_tree($list,'id','fid'); //详细参数见手册
$list=$this->findChild($list);
dump($list);
}
protected function findChild($arr){
static $tree=array();
foreach ($arr as $key=>$val){
$tree[]=$val;
if (isset($val['_child'])){
$this->findChild($val['_child']);
}
}
return $tree;
}/**
* 把返回的数据集转换成Tree
* @access public
* @param array $list 要转换的数据集
* @param string $pid parent标记字段
* @param string $level level标记字段
* @return array
*/
function list_to_tree($list, $pk='id',$pid = 'pid',$child = '_child',$root=0) {
// 创建Tree
$tree = array();
if(is_array($list)) {
// 创建基于主键的数组引用
$refer = array();
foreach ($list as $key => $data) {
$refer[$data[$pk]] =& $list[$key];
}
foreach ($list as $key => $data) {
// 判断是否存在parent
$parentId = $data[$pid];
if ($root == $parentId) {
$tree[] =& $list[$key];
}else{
if (isset($refer[$parentId])) {
$parent =& $refer[$parentId];
$parent[$child][] =& $list[$key];
}
}
}
}
return $tree;
}
/**
* 对查询结果集进行排序
* @access public
* @param array $list 查询结果
* @param string $field 排序的字段名
* @param array $sortby 排序类型
* asc正向排序 desc逆向排序 nat自然排序
* @return array
*/
function list_sort_by($list,$field, $sortby='asc') {
if(is_array($list)){
$refer = $resultSet = array();
foreach ($list as $i => $data)
$refer[$i] = &$data[$field];
switch ($sortby) {
case 'asc': // 正向排序
asort($refer);
break;
case 'desc':// 逆向排序
arsort($refer);
break;
case 'nat': // 自然排序
natcasesort($refer);
break;
}
foreach ( $refer as $key=> $val)
$resultSet[] = &$list[$key];
return $resultSet;
}
return false;
}
/**
* 在数据列表中搜索
* @access public
* @param array $list 数据列表
* @param mixed $condition 查询条件
* 支持 array('name'=>$value) 或者 name=$value
* @return array
*/
function list_search($list,$condition) {
if(is_string($condition))
parse_str($condition,$condition);
// 返回的结果集合
$resultSet = array();
foreach ($list as $key=>$data){
$find = false;
foreach ($condition as $field=>$value){
if(isset($data[$field])) {
if(0 === strpos($value,'/')) {
$find = preg_match($value,$data[$field]);
}elseif($data[$field]==$value){
$find = true;
}
}
}
if($find)
$resultSet[] = &$list[$key];
}
return $resultSet;
}

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1369
1369
 52
52
 Fragen Sie das Mindestgewicht im Teilbaum ab Knoten X und höchstens Abstand D ab
Aug 25, 2023 am 11:25 AM
Fragen Sie das Mindestgewicht im Teilbaum ab Knoten X und höchstens Abstand D ab
Aug 25, 2023 am 11:25 AM
Bei der Computerprogrammierung ist es manchmal erforderlich, das Mindestgewicht eines Teilbaums zu ermitteln, der von einem bestimmten Knoten stammt, vorausgesetzt, der Teilbaum darf keine Knoten enthalten, die mehr als D Einheiten vom angegebenen Knoten entfernt sind. Dieses Problem tritt in verschiedenen Bereichen und Anwendungen auf, darunter in der Graphentheorie, baumbasierten Algorithmen und der Netzwerkoptimierung. Ein Teilbaum ist eine Teilmenge einer größeren Baumstruktur, wobei der angegebene Knoten als Wurzelknoten des Teilbaums dient. Ein Teilbaum enthält alle Nachkommen des Wurzelknotens und deren Verbindungskanten. Die Gewichtung eines Knotens bezieht sich auf einen bestimmten, diesem Knoten zugewiesenen Wert, der seine Wichtigkeit, Wichtigkeit oder andere relevante Metriken darstellen kann. Bei diesem Problem besteht das Ziel darin, das Mindestgewicht aller Knoten in einem Teilbaum zu ermitteln und gleichzeitig den Teilbaum auf Knoten zu beschränken, die höchstens D Einheiten vom Wurzelknoten entfernt sind. Im folgenden Artikel werden wir uns mit der Komplexität des Minings von Mindestgewichten aus Teilbäumen befassen
 Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind?
Aug 15, 2023 pm 05:57 PM
Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind?
Aug 15, 2023 pm 05:57 PM
Wie implementiert man die Funktionen zum Kopieren und Ausschneiden von Knoten von Mind Maps über Vue und jsmind? Mindmap ist ein gängiges Denkwerkzeug, das uns helfen kann, unsere Gedanken zu ordnen und unsere Denklogik zu ordnen. Die Funktionen zum Kopieren und Ausschneiden von Knoten sind häufig verwendete Vorgänge in Mind Maps, mit denen wir vorhandene Knoten bequemer wiederverwenden und die Effizienz der Denkorganisation verbessern können. In diesem Artikel werden wir die beiden Tools Vue und jsmind verwenden, um die Funktionen zum Kopieren und Ausschneiden von Knoten der Mind Map zu implementieren. Zuerst müssen wir Vue und jsmind installieren und erstellen
 Was ist die Methode zum Löschen eines Knotens in js?
Sep 01, 2023 pm 05:00 PM
Was ist die Methode zum Löschen eines Knotens in js?
Sep 01, 2023 pm 05:00 PM
Die Methoden zum Löschen von Knoten in js sind: 1. Die Methode „removeChild()“ wird verwendet, um den angegebenen untergeordneten Knoten vom übergeordneten Knoten zu entfernen. Der erste Parameter ist der zu löschende untergeordnete Knoten der übergeordnete Knoten. 2. Die Methode parentNode.removeChild() kann direkt über den übergeordneten Knoten aufgerufen werden. 3. Die Methode „remove()“ kann den Knoten direkt löschen Das innerHTML-Attribut wird zum Löschen des Knotens verwendet.
 Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
Finden Sie mit dem Floyd-Warshal-Algorithmus den kürzesten Weg zwischen zwei beliebigen Knoten
Sep 20, 2023 pm 02:21 PM
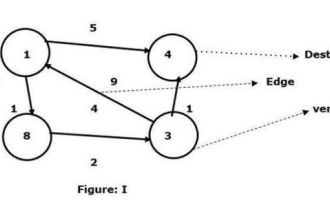
C++ verfügt über ein Makro, das als Codeabschnitt oder erwarteter Wert definiert ist und immer dann wiederverwendet wird, wenn der Benutzer es benötigt. Der Floyd-Walshall-Algorithmus ist der Prozess, den kürzesten Weg zwischen allen Scheitelpunktpaaren in einem gegebenen gewichteten Graphen zu finden. Der Algorithmus folgt einem dynamischen Programmieransatz, um den Minimalgewichtsgraphen zu finden. Lassen Sie uns die Bedeutung des Floyd-Walshall-Algorithmus anhand eines Diagramms verstehen: Nehmen Sie Scheitelpunkt 1 als Quelle und Scheitelpunkt 4 als Ziel und finden Sie den kürzesten Weg zwischen ihnen. Wir haben gesehen, dass es zwei Pfade gibt, die mit dem Zielscheitelpunkt 4 verbunden werden können. 1->4 – die Kante hat ein Gewicht von 51->8->3->4 – das Kantengewicht (1+2+1) ist 4. Im gegebenen Diagramm I sehen wir die kleinste Kante, die zwei Eckpunkte verbindet. Hier also der Scheitelpunkt
 So erstellen, löschen, hängen und ersetzen Sie Elementknoten in js (mit Codebeispielen)
Aug 06, 2022 pm 05:26 PM
So erstellen, löschen, hängen und ersetzen Sie Elementknoten in js (mit Codebeispielen)
Aug 06, 2022 pm 05:26 PM
In diesem Artikel wird hauptsächlich das Erstellen, Löschen, Anhängen und Ersetzen von Elementknoten in js vorgestellt. Ich hoffe, dass er Freunden in Not hilfreich sein wird!
 Überprüft, ob der Pfad zwischen zwei Knoten im angegebenen Diagramm den kürzesten Pfad darstellt
Sep 07, 2023 pm 06:57 PM
Überprüft, ob der Pfad zwischen zwei Knoten im angegebenen Diagramm den kürzesten Pfad darstellt
Sep 07, 2023 pm 06:57 PM
Um zu überprüfen, ob ein gegebener Pfad zwischen zwei Mittelpunkten eines Graphen dem kürzesten Weg entspricht, kann dies berechnet werden, indem das gesamte Kantengewicht entlang des gegebenen Pfades mit dem kürzesten Abstand zwischen Kombinationen derselben Mittelpunkte unter Verwendung eines zuverlässigen kürzesten Pfades verglichen wird, z Dijkstra-Berechnung oder Floyd-Warshall-Berechnung. Wenn alle Kantengewichte auf einem bestimmten Pfad mit der am stärksten eingeschränkten Löschung übereinstimmen, stellt dies den einfachsten Pfad dar. Außerdem: Wenn das Gesamtkantengewicht stärker ausgeprägt ist als der kürzeste Abstand, weist dies darauf hin, dass zwischen den beiden Mittelpunkten im Diagramm ein geringer Abstand besteht. Verwendete Methoden Dijkstras Algorithmus Floyd-Warshall-Algorithmus mit Kantenumkehrkosten Greedy-Algorithmus Die Dijkstra-Berechnung ist wahrscheinlich eine beliebte Graph-Traversal-Berechnung.
 Übersetzen Sie im C-Programm den folgenden Inhalt ins Chinesische: Programm zum Suchen des n-ten Knotens am Ende einer verknüpften Liste
Sep 13, 2023 pm 03:13 PM
Übersetzen Sie im C-Programm den folgenden Inhalt ins Chinesische: Programm zum Suchen des n-ten Knotens am Ende einer verknüpften Liste
Sep 13, 2023 pm 03:13 PM
Bei n Knoten besteht die Aufgabe darin, den n-ten Knoten am Ende der verknüpften Liste zu drucken. Das Programm darf die Reihenfolge der Knoten in der Liste nicht ändern, sondern sollte nur den n-ten Knoten vom letzten Knoten der verknüpften Liste ausdrucken. Beispiel Input-:102030405060 N=3Output-:40 Im obigen Beispiel wird ausgehend vom ersten Knoten die Anzahl der n Knoten durchlaufen, d. h. 10,2030,40,50,60, sodass der drittletzte Knoten 40 ist . Anstatt die gesamte Liste so effizient zu durchlaufen, können Sie dem Ansatz folgen: Holen Sie sich einen temporären Zeiger auf beispielsweise temp des Knotentyps und setzen Sie diesen temporären Zeiger auf den ersten Knoten, auf den der Kopfzeiger zeigt, um den Zähler auf den Knoten in der Liste zu setzen
 Beim Plug-in ChatGPT handelt es sich um einen Knoten, aber nicht um ein Zentrum
Apr 04, 2023 am 11:45 AM
Beim Plug-in ChatGPT handelt es sich um einen Knoten, aber nicht um ein Zentrum
Apr 04, 2023 am 11:45 AM
OpenAI ist ein Knotenpunkt (wenn auch ein wichtiger Knotenpunkt) in der Welt des Roboter-Roboter-Dialogs, aber nicht das Zentrum. ChatGPT hat einen Plugin-Mechanismus eingeführt, was eine sehr spannende Entwicklung darstellt. Alle waren sich einig, dass „ein Betriebssystem geboren wurde“. Diese Aussage ist völlig falsch. OpenAI ist ein Knotenpunkt (wenn auch ein wichtiger Knotenpunkt) in der Welt des Roboter-Roboter-Dialogs, aber nicht das Zentrum. Ich hatte immer ein Bild im Kopf: eine Welt, in der Roboter mit Robotern sprechen. Menschen chatten mit einem Roboter und lassen den Roboter über seine Roboterfreunde dem Menschen helfen, Aufgaben zu erledigen. Das ChatGPT-Plugin demonstriert die Welt perfekt




