1 Überblick über Entscheidungssteuerung und Bewegungsplanung
Aktuelle Entscheidungssteuerungsmethoden können in drei Kategorien unterteilt werden: sequentielle Planung, verhaltensbewusste Planung und End-to-End-Planung.
- Sequentielle Planung: Die traditionellste Methode, die drei Teile Wahrnehmung, Entscheidung und Kontrolle sind relativ klar;
- verhaltensbewusste Planung: Im Vergleich zur ersten Methode ist das Highlight die Einführung der Mensch-Maschine-Kollaboration Fahren, Fahrzeug-Straßen-Kollaboration und Risikoabschätzung von Fahrzeugen gegenüber der externen dynamischen Umgebung
- End-to-End-Planung: DL- und DRL-Technologie wird mit Hilfe einer großen Datenmenge trainiert Informationen von sensorischen Informationen wie Bildern bis hin zu Fahrzeugsteuerungseingaben wie Lenkradwinkeln ist heutzutage eine der beliebtesten Methoden.
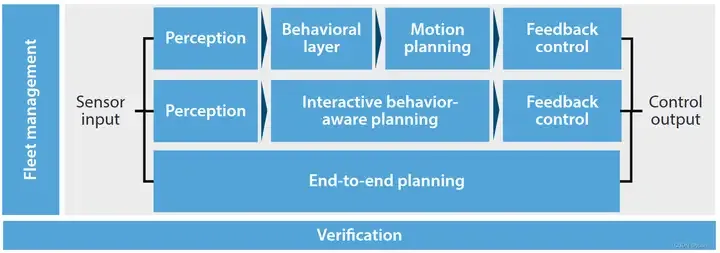
In diesem Artikel wird die sequentielle Planung vorgestellt, der Wahrnehmungssteuerungsprozess autonomer Fahrzeuge gemäß der gesamten Entscheidungssteuerungssequenz beschrieben und abschließend die oben genannten zu lösenden Probleme kurz zusammengefasst.
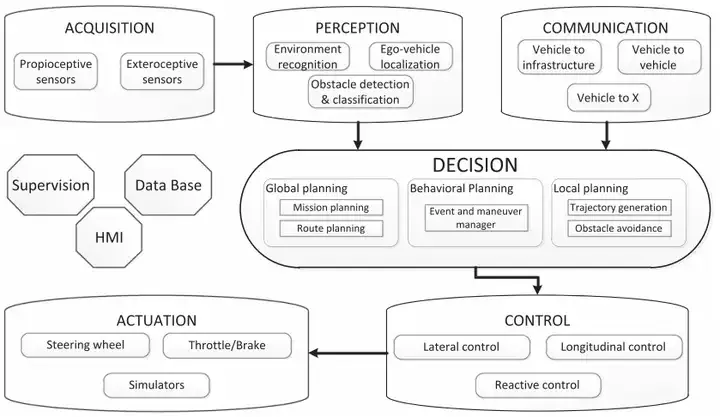
Steuerungsarchitektur für automatisierte Fahrzeuge
2 Überblick über die Pfadplanung
Der sequentielle Planungsprozess wird kurz zusammengefasst als Pfadplanung->Entscheidungsprozess->Fahrzeugsteuerung, der Pfad Die in diesem Artikel beschriebene Planung gehört zum ersten und dritten Schritt.
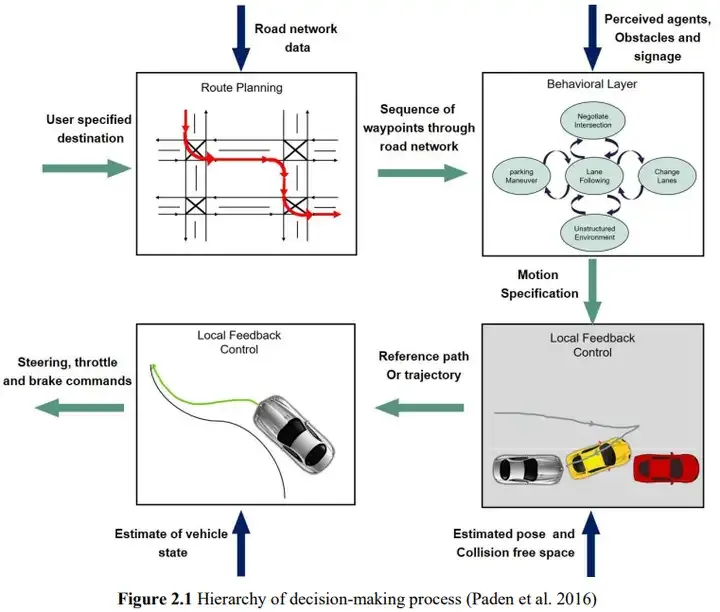
https://www.php.cn/link/aa7d66ed4b1c618962d406535c4d282a
In Bezug auf das Problem der Trajektorienerzeugung für unbemannte Fahrzeuge gibt es zwei Arten: Methode zur direkten Trajektorienerzeugung und Weg-Geschwindigkeits-Zerlegungsmethode Im Vergleich zum ersten Typ ist die Pfadgeschwindigkeit weniger schwierig und wird daher häufiger verwendet.
2.1 Arten der Pfadplanung
Die Pfadplanung kann in vier Hauptkategorien unterteilt werden: Algorithmen basierend auf „Sampling“ dargestellt durch PRM und RRT, Algorithmen basierend auf „Suche“ dargestellt durch A* und D*, die Trajektoriengenerierung Algorithmus basierend auf Interpolation Anpassung, dargestellt durch die β-Spline-Kurve, und dem optimalen Steuerungsalgorithmus für die lokale Pfadplanung, dargestellt durch MPC. Dieser Abschnitt wird in der oben genannten Reihenfolge erläutert:
Ein Überblick über den Algorithmus der Bewegungsplanungstechnologie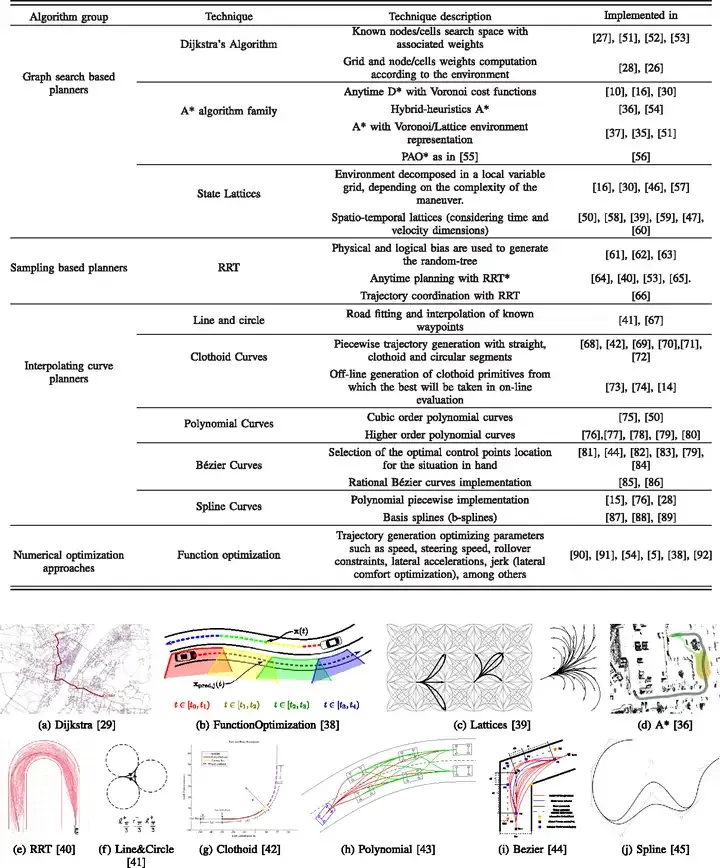
3.1.1 Grundlegender Algorithmus PRM und RRT
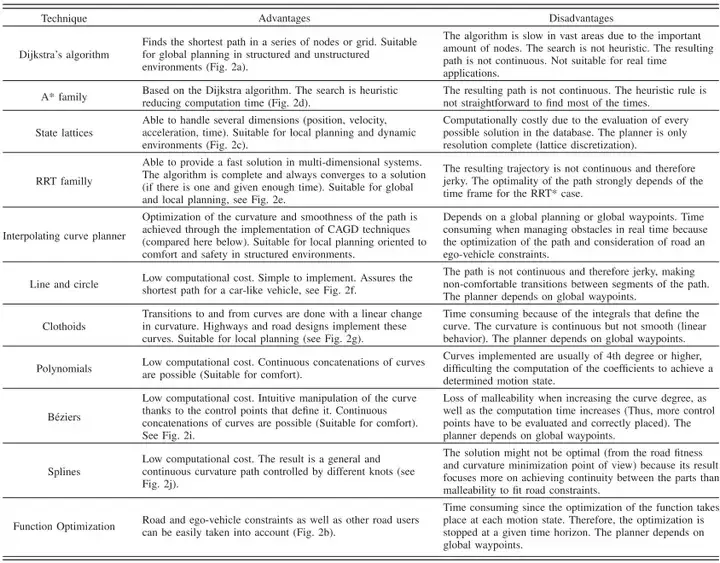(1) PRM
PRM-Algorithmus (Probabilistische Roadmap). PRM besteht hauptsächlich aus zwei Schritten, einem ist die Lernphase und der andere ist die Abfragephase.
Der erste Schritt, die Lernphase: Stichproben Sie gleichmäßig und zufällig n Punkte im sicheren Bereich im Zustandsraum ab und löschen Sie die Punkte, an denen die Stichproben auf die Hindernisse fallen. Verbinden Sie dann die benachbarten Punkte, führen Sie eine Kollisionserkennung durch und eliminieren Sie nicht -Kollisionsfreie Verbindungen und schließlich ein verbundenes Diagramm erhalten.
Zweiter Schritt, Abfragephase: Verwenden Sie für ein gegebenes Paar aus Anfangs- und Zielzuständen die im vorherigen Schritt konstruierten Stichprobenknoten und die Kontinuität und verwenden Sie Graphsuchmethoden (Dijkstra oder A*), um einen realisierbaren Pfad zu finden.
Nach Abschluss der PRM-Konstruktion kann es zur Lösung von Bewegungsplanungsproblemen in verschiedenen Anfangs- und Zielzuständen verwendet werden, diese Funktion ist jedoch für die Bewegungsplanung unbemannter Fahrzeuge nicht erforderlich. Darüber hinaus erfordert PRM präzise Verbindungen zwischen Zuständen, was bei Bewegungsplanungsproblemen mit komplexen Differentialbeschränkungen sehr schwierig ist.
(2) RRT
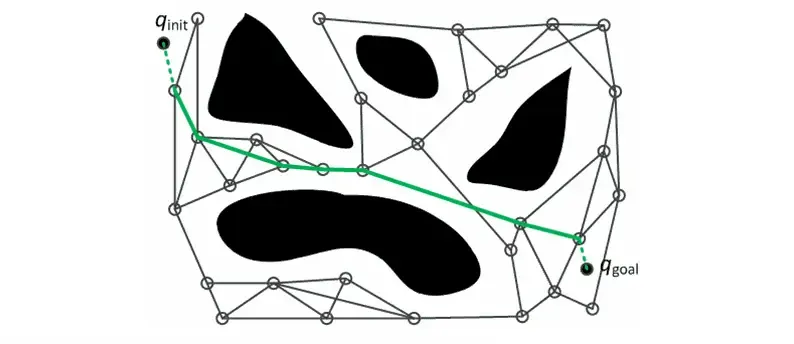RRT-Algorithmus (Rapidly-Exploring Random Tree). RRT stellt eigentlich eine Reihe von Algorithmen dar, die auf der Idee des
zufällig wachsenden Baums
basieren. Es ist derzeit der am weitesten verbreitete Algorithmus mit den meisten Optimierungsvarianten im Bereich der Robotik
① Bauminitialisierung Knotensatz und Kantensatz des Baums, der Knotensatz enthält nur den Anfangszustand und der Kantensatz ist leer
② Baumwachstum: Wenn der Abtastpunkt im sicheren Bereich des Zustandsraums liegt, wählen Sie den Knoten aus, der dem Abtastpunkt im aktuellen Baum am nächsten liegt, und erweitern Sie ihn auf den Abtastpunkt Die Flugbahn ist nicht mit dem Hindernis verbunden. Wenn ein Objekt kollidiert, wird die Flugbahn zum Kantensatz des Baums hinzugefügt und der Endpunkt der Flugbahn wird zum Knotensatz des Baums hinzugefügt.
③ Wiederholen Sie Schritt ②, bis er erweitert ist Im Vergleich zum ungerichteten Diagramm von PRM wird bei RRT eine Baumstruktur mit dem Anfangszustand als Wurzelknoten und dem Zielzustand als Blattknoten erstellt konstruiert werden.
RRT erfordert keine präzisen Verbindungen zwischen Zuständen und eignet sich besser zur Lösung von Bewegungsdynamikproblemen wie der Bewegungsplanung unbemannter Fahrzeuge.
3.1.2 Probleme und Lösungen der Probenahmemethode
Lösungseffizienz und ob es die optimale Lösung ist. Der Grund, warum PRM und RRT probabilistische Vollständigkeit besitzen, liegt darin, dass sie fast alle Positionen im Konfigurationsraum durchlaufen.
(1) Lösungseffizienz
Im Hinblick auf die Verbesserung der Lösungseffizienz besteht die Kernidee der RRT-Optimierung darin, den Baum in den offenen Bereich zu führen, d Vermeiden Sie wiederholte Kontrollen von Knoten an Hindernissen. Dies verbessert die Effizienz. Hauptlösung:
① Gleichmäßige Abtastung
Der Standard-RRT-Algorithmus tastet den Zustandsraum gleichmäßig und zufällig ab. Die Wahrscheinlichkeit, dass ein Knoten im aktuellen Baum eine Expansion erhält, ist proportional zu seiner Voronoi-Regionsfläche Der Baum bewegt sich in Richtung des Zustands. Der leere Bereich des Raums wächst, der freie Bereich, der den Zustandsraum gleichmäßig ausfüllt. Der
RRT-Connect-Algorithmus erstellt gleichzeitig zwei Bäume, beginnend mit dem
Anfangszustand bzw. dem Zielzustand. Wenn die beiden Bäume zusammenwachsen, wird eine praktikable Lösung gefunden. Go-Biaing fügt den Zielzustand in einem bestimmten Verhältnis in die Zufallsstichprobensequenz ein, wodurch der Baum sich in Richtung des Zielzustands ausdehnt, die Lösung beschleunigt und die Lösungsqualität verbessert wird. heuristisches RRT verwendet eine heuristische Funktion, um die Wahrscheinlichkeit zu erhöhen, Knoten mit niedrigen Erweiterungskosten abzutasten und die Kosten jedes Knotens im Baum zu berechnen. In komplexen Umgebungen ist die Definition der Kostenfunktion jedoch schwierig. f Die voreingenommene Stichprobenmethode diskretisiert zunächst den Zustandsraum in ein Gitter und berechnet dann mithilfe des Dijkstra-Algorithmus die Kosten für jedes Gitter. Der Kostenwert der Punkte im Bereich des Gitters ist gleich diesem Wert , wodurch eine heuristische Funktion konstruiert wird.
② Optimierte Distanzmetrik
Distance wird verwendet, um die Kosten des Pfads zwischen zwei Konfigurationen zu messen, hilft bei der Generierung einer heuristischen Kostenfunktion und gibt die Richtung des Baums vor. Allerdings ist die Entfernungsberechnung schwierig, wenn Hindernisse berücksichtigt werden. Die Definition der Entfernung in der Bewegungsplanung folgt einer Definition, die der euklidischen Entfernung ähnelt. RG-RRT (Rechability Guided RRT) kann die Auswirkungen einer ungenauen Entfernung auf die RRT-Erkundungsfähigkeit beseitigen. Es muss die erreichbare Menge von Knoten im Baum berechnen, wenn die Entfernung vom Abtastpunkt zum Knoten größer ist als die erreichbare Menge Knoten, Abstand, Knoten können zur Erweiterung ausgewählt werden.
③ Reduzieren Sie die Anzahl der Kollisionsprüfungen
Einer der Effizienzengpässe der Kollisionsprüfungs-Stichprobenmethode besteht darin, dass der übliche Ansatz darin besteht, den Pfad in gleichen Abständen zu diskretisieren und dann bei jedem Kollisionsprüfungen für die Konfiguration durchzuführen Punkt. Auflösung vollständig RRT erhält die Erweiterungswahrscheinlichkeit durch
Reduzierung von Knoten
in der Nähe von Hindernissen. Es diskretisiert den Eingaberaum und verwendet ihn nur einmal für eine bestimmte Knoteneingabe, wenn die Trajektorie mit einem Hindernis kollidiert wird dem Knoten hinzugefügt. Je höher der Strafwert ist, desto geringer ist die Wahrscheinlichkeit, dass der Knoten erweitert wird. Dynamisches Domänen-RRT und adaptives dynamisches Domänen-RRT beschränken den Abtastbereich auf den lokalen Raum, in dem sich der aktuelle Baum befindet, um zu verhindern, dass Knoten in der Nähe von Hindernissen wiederholte Erweiterungsfehler erleiden, und verbessern die Algorithmuseffizienz. ④ Verbessern Sie die Echtzeitleistung.
Jedes Mal, wenn RRT zunächst schnell ein RRT erstellt, eine realisierbare Lösung erhält und deren Kosten aufzeichnet, fährt dann die Stichprobe fort, fügt jedoch nur Knoten ein, die zur Reduzierung der Kosten der realisierbaren Lösung von Vorteil sind den Baum, wodurch nach und nach eine bessere realisierbare Lösung erhalten wird. Bei der Neuplanung wird die gesamte Planungsaufgabe in mehrere zeitgleiche Unteraufgabensequenzen zerlegt und die nächste Aufgabe geplant, während die aktuelle Aufgabe ausgeführt wird. (2) Es gibt hauptsächlich die folgenden Methoden, um das
Optimalitätsproblem
zu lösen:
RGG-Algorithmus (zufälliger geometrischer Graph): ein PRM mit asymptotischen optimalen Eigenschaften, der den Standard-PRM und RRT basierend auf der Theorie des zufälligen geometrischen Graphen verbessert. RRG- und RRT-Algorithmen tasten zufällig n Punkte im Zustandsraum ab und verbinden die Punkte mit einem Abstand kleiner als r(n), um RGG zu bilden.
RRT*-Algorithmus: Führen Sie den Schritt „Wiederverbindung“ basierend auf RRG ein, um zu prüfen, ob der neu eingefügte Knoten als übergeordneter Knoten seines benachbarten Punkts die Kosten seines benachbarten Punkts verringert. Wenn dies der Fall ist, entfernen Sie den ursprünglichen übergeordneten und untergeordneten Knoten Der benachbarte Punkt, der den aktuellen Einfügepunkt als übergeordneten Knoten verwendet, ist der RRT*-Algorithmus. LBT-RRT-Algorithmus: Eine große Anzahl von Knotenverbindungen und lokalen Anpassungen machen PRM und RRT sehr ineffizient. Der LBT-RRT-Algorithmus kombiniert die RRG- und RRT*-Algorithmen, um unter der Prämisse, asymptotische Optimalität zu erreichen, eine höhere Effizienz zu erzielen.
3.2 Suchbasierter Algorithmus
Die Grundidee besteht darin, den Zustandsraum auf eine bestimmte Weise in ein Diagramm zu diskretisieren und dann verschiedene heuristische Suchalgorithmen zu verwenden, um nach durchführbaren Lösungen oder sogar zu suchen optimale Lösungen , dieser Kategoriealgorithmus ist relativ ausgereift.
Die Grundlage des suchbasierten Algorithmus ist das Zustandsgitter. Das Zustandsgitter ist eine Diskretisierung des Zustandsraums. Es besteht aus einem Zustandsknoten und einem Bewegungsprimitiv, das vom Knoten ausgeht und den benachbarten Knoten erreicht. Ein Zustandsknoten kann seine Bewegungsprimitivtransformationen an einen anderen Zustandsknoten weitergeben. Das Zustandsgitter wandelt den ursprünglichen kontinuierlichen Zustandsraum in ein Suchdiagramm um. Das Bewegungsplanungsproblem besteht darin, nach einer Reihe von Bewegungsprimitiven zu suchen, die den Anfangszustand in den Zielzustand im Diagramm umwandeln. Nach der Erstellung des Zustandsgitters können Sie die Diagrammsuche verwenden Algorithmus zur Suche nach der optimalen Flugbahn.
3.2.1 Konstruktion der Grundalgorithmen Dijkstra und A*
Der Dijkstra-Algorithmus durchquert den gesamten Konfigurationsraum, ermittelt den Abstand zwischen jeweils zwei Gittern und wählt schließlich den kürzesten Weg vom Startpunkt zum Zielpunkt mit Breite aus Die Prioritätsnatur führt zu einer sehr geringen Effizienz dieses Algorithmus, d. h. der Entfernung vom gesuchten Knoten zum Zielknoten, und eine erneute Suche auf dieser Grundlage kann die durch die globale Suche verursachte Ineffizienz vermeiden Wie in der folgenden Abbildung gezeigt, ist Rot der Suchbereich.
Abbildung 6: Vergleich der Auswirkungen von A*- und Dijkstra-Algorithmen
3.2.2 Probleme und Vorschläge für Suchmethoden
Diese Art von Algorithmus muss ebenso wie stichprobenbasierte Algorithmen effizient und effizient sein optimale sexuelle Optimierung.
Im Hinblick auf die Verbesserung der Effizienz ist A* selbst ein statischer Planungsalgorithmus, eine Erweiterung des A*-Algorithmus, der die Suchrichtung durch Erhöhen der Gewichtung der heuristischen Funktion weiterleitet Die Geschwindigkeit ist sehr hoch, fällt jedoch leicht in lokale Minima und kann die global optimale Lösung nicht garantieren.
Bei fahrenden Fahrzeugen kann die Verwendung des Ableitungsalgorithmus D (dynamisch A) von A* die Effizienz erheblich verbessern. Dieser Algorithmus basiert ebenfalls auf dynamischer Programmierung und kann Situationen bewältigen, in denen sich die Kosten der Bewegungsprimitive des Zustandsgitters ändern Knoten. D*-Lite wurde auf Basis von LPA
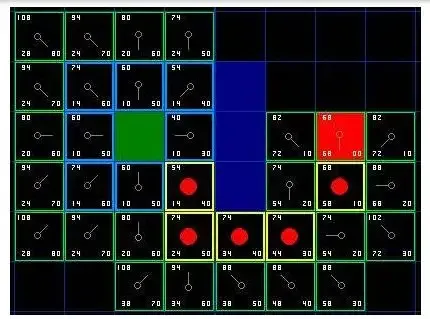
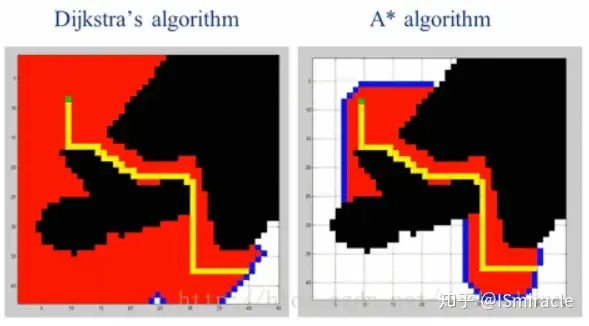
entwickelt und kann die gleichen Ergebnisse wie D* erzielen, jedoch mit höherer Effizienz.
Bei der Suche nach optimalen Lösungen ist ARA* ein jederzeitiger Suchalgorithmus, der auf der Grundlage von Weighted A* entwickelt wurde. Er ruft den Weighted A*-Algorithmus mehrmals auf und reduziert das Gewicht der heuristischen Funktion, sodass der Algorithmus Durch die Einführung der Menge INCONS kann jeder Zyklus weiterhin die Informationen des vorherigen Zyklus verwenden, um den Pfad zu optimieren und sich schrittweise der optimalen Lösung zu nähern.
Um die Effizienz und Optimalität des Algorithmus in Einklang zu bringen, schlugen Sandinaine et al. den MHA*-Algorithmus vor, der mehrere heuristische Funktionen einführte, um sicherzustellen, dass eine der heuristischen Funktionen die optimale Lösung finden kann, wenn sie allein verwendet wird, also durch Koordinierung der Pfadkosten Die von verschiedenen heuristischen Funktionen generierten Werte können die Effizienz und Optimalität des Algorithmus berücksichtigen. DMHA generiert auf Basis von MHA online und in Echtzeit entsprechende heuristische Funktionen und vermeidet so das lokale Minimalproblem. 3.3 Algorithmus basierend auf Interpolationsanpassung Die Kurvenanpassungsmethode erstellt den Weg, auf dem das Smart-Auto fahren wird, was eine bessere Kontinuität und eine höhere Differenzierbarkeit bieten kann. Die spezifische Methode ist wie folgt:
Dubins-Kurve und Reeds-and-Sheep-Kurve (RS) sind die kürzesten Pfade, die zwei beliebige Punkte im Konfigurationsraum verbinden, entsprechend den Situationen ohne Umkehrung bzw. mit Umkehrung. Sie bestehen alle aus Bögen mit maximaler Krümmung und geraden Linien. An der Verbindung zwischen dem Bogen und der geraden Linie besteht eine Krümmungsunterbrechung. Wenn ein tatsächliches Fahrzeug auf einer solchen Kurve fährt, muss es an der Unterbrechung anhalten und das Lenkrad anpassen der Krümmung, um weiterzufahren.
Polynominterpolationskurve
ist die am häufigsten verwendete Methode. Sie kann Polynomkoeffizienten festlegen, indem sie die Anforderungen von Knoten erfüllt und eine bessere kontinuierliche Differenzierbarkeit erhält. Polynome vierter Ordnung werden häufig zur Steuerung von Längsbeschränkungen verwendet Wird zur Steuerung von Längsbeschränkungen verwendet. Polynome werden häufig bei der Steuerung von Querbeschränkungen verwendet, und Polynome dritter Ordnung werden auch bei Überholtrajektorien verwendet.
Spline-Kurve hat einen geschlossenen Ausdruck und kann leicht die Kontinuität der Krümmung gewährleisten. β-Spline-Kurven können eine Krümmungskontinuität erreichen, und kubische Bezier-Kurven können die Kontinuität und Begrenztheit der Krümmung sicherstellen, und der Rechenaufwand ist relativ gering. Die η^3-Kurve [43] ist eine Spline-Kurve siebter Ordnung, die sehr gute Eigenschaften aufweist: Kontinuität der Krümmung und Kontinuität der Krümmungsableitungen, was für Hochgeschwindigkeitsfahrzeuge von großer Bedeutung ist.
3.4 Algorithmen, die auf optimaler Steuerung basieren
Algorithmen, die auf optimaler Steuerung basieren, werden in die Pfadplanung eingeteilt, hauptsächlich weil MPC eine lokale Pfadplanung zur Vermeidung von Hindernissen durchführen kann. Darüber hinaus besteht die Funktion von MPC darin, die Flugbahn zu verfolgen Neben den notwendigen Dynamiken und kinematischen Einschränkungen sollten bei den berücksichtigten Themen auch Komfort, Unsicherheit der sensorischen Informationen, Unsicherheit der zukünftigen Kommunikation zwischen Fahrzeugen und bei der Planung lokaler Trajektorien berücksichtigt werden. Der Fahrer kann auch in den Regelkreis einbezogen werden. Die oben genannten Unsicherheitsprobleme und die Einbindung des Treibers in den Regelkreis werden in Abschnitt 4 erörtert. Das MPC-Studium beginnt hauptsächlich mit zwei Aspekten: Optimierungstheorie und Ingenieurpraxis. Für Ersteres empfehle ich Convex Optimization Algorithms von Dimitri P. Bertsekas und Model Predictive Control: Theory, Computation, and Design von James B. Rawlings. Im chinesischen Bereich ist das Optimierungsbuch von Lehrer Liu Haoyang persönlich der Meinung, dass es relativ klar und leicht verständlich ist. Für Letzteres ist zunächst das selbstfahrende MPC-Buch von Lehrer Gong Jianwei dringend zu empfehlen. In der alten Version des Buches gab es Probleme mit der Demo, die jedoch in der neuen Version alle gelöst wurden.
Es gibt viele Vorhersagemodelle, die von MPC verwendet werden: wie Faltungs-Neuronale Netzwerke, Fuzzy-Steuerung, Zustandsraum usw. Unter diesen ist die Zustandsraummethode das am häufigsten verwendete. MPC kann kurz ausgedrückt werden als: Wenn die erforderlichen dynamischen, kinematischen usw. Einschränkungen erfüllt sind, wird die optimale Lösung des Modells mit numerischen Mitteln gelöst. Die optimale Lösung ist die Steuervariable der Zustandsgleichung, beispielsweise der Lenkradwinkel usw. und wenden Sie die Steuergröße auf das Automodell an, um die erforderlichen Zustandsgrößen wie Geschwindigkeit, Beschleunigung, Koordinaten usw. zu erhalten.
Aus der obigen Beschreibung ist ersichtlich, dass der Schlüssel zu MPC in der Einrichtung und Lösung des Modells liegt. Die Frage, wie die Einrichtung des Modells gleichermaßen vereinfacht und die Effizienz der Lösung verbessert werden kann, hat oberste Priorität. Das Fahrzeug nimmt unter verschiedenen Steuereingaben unterschiedliche Flugbahnen an, und jede Flugbahn entspricht einem Zielfunktionswert. Das unbemannte Fahrzeug verwendet einen Lösungsalgorithmus, um die dem minimalen Zielfunktionswert entsprechende Steuergröße zu ermitteln und diese auf das oben genannte Fahrzeug anzuwenden , wie in der folgenden Abbildung dargestellt:
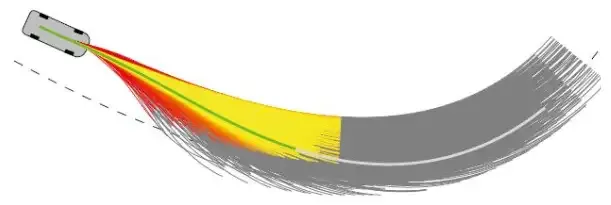
Um die Schwierigkeit der Modellierung zu verringern, werden zur Modellierung auch künstliche potentielle Energiefelder verwendet. Die Grundidee künstlicher potentieller Energiefelder ähnelt elektrischen Feldern Hindernisse auf der Straße ähneln den Feldquellen in elektrischen Feldern. Ladungen mit unterschiedlicher Ladungspolarität. Die potenzielle Energie an Hindernissen (dynamisch, statisch) ist höher und das unbemannte Fahrzeug bewegt sich in Richtung einer Position mit niedriger potenzieller Energie.
4 Open-Source-Projekte Kubischer Spline-Planer
State Lattice Planner
Frenet Frame Trajectory-
- 5 Lernmethoden
-
- Der Lernkontext für den Einstieg in neue Bereiche ist:
Ingenieurwesen- ,
Theorie- und
Vision- Troika gehen Hand in Hand und übernehmen die Pfadplanung als Ein Beispiel:
- 5.1 Engineering
-
bezieht sich auf das Verständnis des Inhalts jedes Pfadplanungsalgorithmus, während gleichzeitig der Inhalt jedes Algorithmus aus der
Breite verstanden wird und gleichzeitig die Details jedes Algorithmus aus der Tiefe gelernt werden
. Bezüglich Algorithmen im Bereich der Pfadplanung gibt es derzeit kein umfassendes Tutorial, Gong Jianweis NMPC-Bewegungsplanung kann jedoch als Referenz dienen.
5.2 Theorie bezieht sich auf das Verständnis der mathematischen Prinzipien, die die Funktionsweise dieser Algorithmen unterstützen, und der Gründe, warum diese Algorithmen generiert werden (mathematische Perspektive).
Konstruieren Sie die Zielfunktion und die Randbedingungen und ermitteln Sie gleichzeitig den Extremwert, um die optimale Steuervariable (Pfad) zu erhalten, die zur Optimierungstheorie gehört;
Gemeinsame Newton-Methode, Methode des steilsten Abstiegs usw Das Wesentliche dieser numerischen Lösungsmethoden ist die numerische Lösung, die zur numerischen Analyse gehört. Die im Lösungsprozess sichtbare abgeleitete Jacobi-Matrix ist die Vektornorm in der Beurteilungsbedingung usw. dienen im Wesentlichen der Konvertierung eindimensionaler numerischer Lösungen, die hohe Dimensionen erreichen und zur Matrixtheorie
gehören.
5.3 Vision
bezieht sich auf das Verständnis der Hauptanwendungen der Pfadplanung in der wissenschaftlichen Forschung und in Unternehmen, unter Verwendung wissenschaftlicher Forschungsdokumente und Ergebnisberichte usw. -
6 Zusammenfassung
- Dieser Artikel stellt den Grundriss der aktuellen Pfadplanung vor und versteht die aktuellen Pfadplanungsmethoden. Der Inhalt ist sehr komplex und es ist schwierig, alles in kurzer Zeit ohne praktische Anwendungsorientierung zu lernen. Sie können sich nur dann auf das Lernen konzentrieren, wenn es nötig ist.
-
Das obige ist der detaillierte Inhalt vonÜberblick über die Pfadplanung: Basierend auf Probenahme, Suche und Optimierung, fertig!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
