Zeigen Sie LLM die Kausalkette und es lernt die Axiome.
KI hilft Mathematikern und Wissenschaftlern bereits bei der Forschung. Beispielsweise hat der berühmte Mathematiker Tao Zhexuan wiederholt seine Forschungs- und Erkundungserfahrungen mit Hilfe von GPT und anderen KI-Tools geteilt. Damit KI in diesen Bereichen konkurrenzfähig sein kann, sind starke und zuverlässige Fähigkeiten zum Kausaldenken unerlässlich. Die in diesem Artikel vorgestellte Forschung ergab, dass Transformer-Modelle, die auf Demonstrationen des kausalen Transitivitätsaxioms für kleine Graphen trainiert wurden, auf das Transitivitätsaxiom für große Graphen verallgemeinern können. Mit anderen Worten: Wenn Transformer lernt, einfache kausale Überlegungen anzustellen, kann es für komplexere kausale Überlegungen verwendet werden. Das vom Team vorgeschlagene Axiom-Trainings-Framework ist ein neues Paradigma zum Erlernen des kausalen Denkens auf der Grundlage passiver Daten, das zum Erlernen beliebiger Axiome verwendet werden kann, sofern die Demonstration ausreichend ist. Kausales Denken kann als eine Reihe von Denkprozessen definiert werden, die vordefinierten Axiomen oder Regeln speziell für die Kausalität entsprechen. Beispielsweise können die Regeln der d-Trennung (gerichtete Trennung) und der Do-Kalküle als Axiome betrachtet werden, während die Spezifikationen eines Collider-Sets oder eines Backdoor-Sets als aus den Axiomen abgeleitete Regeln betrachtet werden können. Im Allgemeinen verwendet der kausale Rückschluss Daten, die Variablen in einem System entsprechen. Axiome oder Regeln können in Form von induktiven Verzerrungen durch Regularisierung, Modellarchitektur oder spezifische Variablenauswahl in Modelle des maschinellen Lernens integriert werden. Basierend auf den Unterschieden in den verfügbaren Datentypen (Beobachtungsdaten, Interventionsdaten, kontrafaktische Daten) definiert die von Judea Pearl vorgeschlagene „Kausalleiter“ mögliche Arten kausaler Schlussfolgerungen. Da Axiome der Eckpfeiler der Kausalität sind, müssen wir uns fragen, ob wir Modelle des maschinellen Lernens direkt verwenden können, um Axiome zu lernen. Das heißt, was wäre, wenn der Weg, Axiome zu lernen, nicht darin besteht, Daten zu lernen, die durch einen Datengenerierungsprozess gewonnen wurden, sondern direkt darin, symbolische Demonstrationen von Axiomen zu lernen (und damit kausales Denken zu lernen)? Im Vergleich zu aufgabenspezifischen Kausalmodellen, die unter Verwendung spezifischer Datenverteilungen erstellt wurden, hat ein solches Modell einen Vorteil: Es kann kausale Schlussfolgerungen in einer Vielzahl unterschiedlicher nachgelagerter Szenarien ziehen. Dieses Problem wird immer wichtiger, da Sprachmodelle die Fähigkeit erlangen, in natürlicher Sprache ausgedrückte symbolische Daten zu lernen. Tatsächlich wurde in einigen neueren Untersuchungen untersucht, ob große Sprachmodelle (LLMs) in der Lage sind, kausale Inferenzen durchzuführen, indem sie Benchmarks erstellen, die kausale Inferenzprobleme in natürlicher Sprache kodieren. Forschungsteams von Microsoft, MIT und dem Indian Institute of Technology Hyderabad (IIT Hyderabad) haben ebenfalls einen wichtigen Schritt in diese Richtung gemacht: Sie schlagen eine Methode zum Erlernen des Kausaldenkens durch axiomatisches Training vor . 
🔜
- Sie gehen davon aus, Das kausale Axiom kann als folgendes symbolisches Tupel ausgedrückt werden: „Prämisse, Hypothese, Ergebnis“. Unter ihnen bezieht sich Hypothese auf die Hypothese, das heißt, eine kausale Aussage ist die Prämisse, die sich auf alle relevanten Informationen bezieht, die verwendet werden, um zu bestimmen, ob die Aussage „wahr“ ist. Das Ergebnis kann ein einfaches „Ja“ oder „Nein“ sein.
-
Zum Beispiel kann das Collider-Axiom aus dem Artikel „Können große Sprachmodelle aus Korrelation auf Kausalität schließen?“ ausgedrückt werden als:
, und die Schlussfolgerung lautet „Ja“.
Basierend auf dieser Vorlage kann eine große Anzahl synthetischer Tupel generiert werden, indem Variablennamen, Variablennummern, Variablenreihenfolge usw. geändert werden.
Um Transformer zum Erlernen kausaler Axiome und zum Implementieren des Axiomtrainings zu verwenden, verwendete das Team die folgenden Methoden zum Erstellen von Datensätzen, Verlustfunktionen und Positionseinbettungen. 🔜 ( Ja oder nein). Um den Trainingsdatensatz zu erstellen, zählt das Team alle möglichen Tupel {(P, H, L)}_N unter bestimmten Variableneinstellungen X, Y, Z, A auf, wobei P die Prämisse und H die Hypothese ist und L die Bezeichnung ist (Ja oder nein).
Wenn eine Prämisse P auf der Grundlage eines Kausaldiagramms gegeben ist und die Hypothese P durch die Verwendung eines bestimmten Axioms (einmal oder mehrmals) abgeleitet werden kann, ist die Bezeichnung L „Ja“; andernfalls lautet sie „Nein“. Angenommen, der zugrunde liegende reale Kausalgraph eines Systems hat eine Kettentopologie: X_1 → X_2 → X_3 →・・・→ X_n. Dann ist eine mögliche Prämisse X_1 → X_2 ∧ X_2 → X_3, dann sei X_1 → Die oben genannten Axiome können mehrfach induktiv verwendet werden, um komplexere Trainingstupel zu erzeugen.
Für den Trainingsaufbau erstellen Sie einen synthetischen Datensatz D mit N Axiominstanzen, die durch das Transitivitätsaxiom generiert werden. Jede Instanz in D besteht aus der Form (P_i, H_ij, L_ij),
, wobei n die Anzahl der Knoten in jeder i-ten Prämisse ist. P ist die Prämisse, also ein natürlichsprachlicher Ausdruck einer bestimmten Kausalstruktur (z. B. X verursacht Y, Y verursacht Z); gefolgt von der Frage H (z. B. verursacht X Y?); oder Nein). Dieses Formular deckt effektiv alle Knotenpaare für jede eindeutige Kette in einem bestimmten Kausalgraphen ab. Verlustfunktion kann zu vielversprechenden Ergebnissen führen. Neben Trainings- und Verlustfunktionen ist auch die Wahl der Positionskodierung ein weiterer wichtiger Faktor. Die Positionskodierung kann wichtige Informationen über die absolute und relative Position eines Tokens in einer Sequenz liefern.
Das berühmte Papier „Aufmerksamkeit ist alles, was Sie brauchen“ schlägt eine absolute Positionscodierungsstrategie vor, die periodische Funktionen (Sinus- oder Cosinusfunktionen) verwendet, um diese Codes zu initialisieren.
Absolute Positionskodierung kann bestimmte Werte für alle Positionen beliebiger Sequenzlänge liefern. Einige Untersuchungen zeigen jedoch, dass die absolute Positionscodierung die Längenverallgemeinerungsaufgabe von Transformer nur schwer bewältigen kann. In der lernbaren APE-Variante wird jede Positionseinbettung zufällig initialisiert und mithilfe des Modells trainiert. Diese Methode hat Probleme mit Sequenzen, die länger sind als diejenigen während des Trainings, da die neuen Positionseinbettungen noch nicht trainiert und nicht initialisiert sind.
Interessanterweise haben neuere Erkenntnisse gezeigt, dass das Entfernen von Positionseinbettungen in autoregressiven Modellen die Fähigkeit des Modells zur Längenverallgemeinerung verbessern kann und der Aufmerksamkeitsmechanismus während der autoregressiven Dekodierung ausreicht, um Positionsinformationen zu kodieren. Das Team verwendete verschiedene Positionskodierungen, um deren Einfluss auf die Generalisierung bei kausalen Aufgaben zu verstehen, darunter lernbare Positionskodierung (LPE), sinusförmige Positionskodierung (SPE) und keine Positionskodierung (NoPE).
Um die Generalisierungsfähigkeit des Modells zu verbessern, verwendete das Team auch Datenstörungen, einschließlich Störungen der Länge, des Knotennamens, der Kettenreihenfolge und des Verzweigungsstatus. Folgende Frage stellt sich: Wenn ein Modell anhand dieser Daten trainiert wird, kann das Modell dann lernen, dieses Axiom auf neue Szenarien anzuwenden? Um diese Frage zu beantworten, trainierte das Team mithilfe dieser symbolischen Demonstration des kausal unabhängigen Axioms ein Transformer-Modell von Grund auf. Um die Generalisierungsleistung zu bewerten, trainierten sie eine einfache kausal unabhängige Axiomkette mit Knoten der Größe 3–6 und testeten dann verschiedene Aspekte der Generalisierungsleistung, einschließlich der Längengeneralisierungsleistung (Ketten der Größe 7–15). Namensverallgemeinerung (längere Variablennamen), sequentielle Verallgemeinerung (Ketten mit umgekehrten Kanten oder gemischten Knoten), strukturelle Verallgemeinerung (Graphen mit Verzweigungen). Abbildung 1 zeigt, wie die strukturelle Verallgemeinerung von Transformer bewertet wird. 
Konkret trainierten sie ein Decoder-basiertes Modell mit 67 Millionen Parametern basierend auf der GPT-2-Architektur. Das Modell verfügt über 12 Aufmerksamkeitsebenen, 8 Aufmerksamkeitsköpfe und 512 Einbettungsdimensionen. Sie trainierten das Modell für jeden Trainingsdatensatz von Grund auf. Um die Auswirkungen der Positionseinbettung zu verstehen, untersuchten sie außerdem drei Einstellungen für die Positionseinbettung: sinusförmige Positionskodierung (SPE), erlernbare Positionskodierung (LPE) und keine Positionskodierung (NoPE). Die Ergebnisse sind in Tabelle 1, Abbildung 3 und Abbildung 4 dargestellt. 
Tabelle 1 gibt die Genauigkeit verschiedener Modelle an, wenn sie anhand größerer Kausalketten bewertet werden, die während des Trainings nicht beobachtet wurden. Es ist ersichtlich, dass die Leistung des neuen Modells TS2 (NoPE) mit der Billionen-Parameter-Skala GPT-4 vergleichbar ist. Abbildung 3 zeigt die Ergebnisse der Generalisierungsfähigkeitsbewertung für kausale Sequenzen mit längeren Knotennamen (länger als der Trainingssatz) und die Auswirkungen unterschiedlicher Positionseinbettungen. 
Abbildung 4 bewertet die Generalisierungsfähigkeit bei längeren, unsichtbaren Kausalsequenzen. 
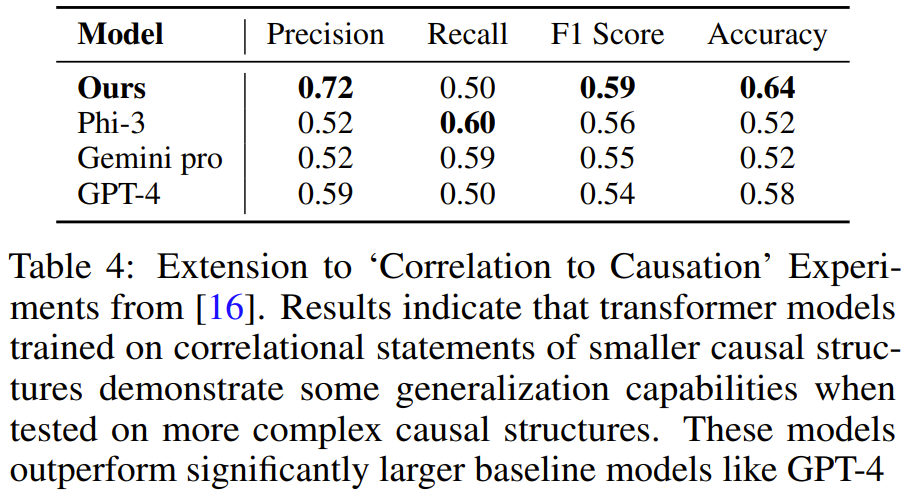
Sie fanden heraus, dass auf einfachen Ketten trainierte Modelle auf mehrere Anwendungen von Axiomen auf größeren Ketten verallgemeinern können, nicht jedoch auf komplexere Szenarien wie sequentielle oder strukturelle Verallgemeinerung. Wenn das Modell jedoch auf einem gemischten Datensatz trainiert wird, der sowohl aus einfachen Ketten als auch aus Ketten mit zufälligen umgekehrten Kanten besteht, lässt sich das Modell gut auf verschiedene Bewertungsszenarien verallgemeinern. Sie erweiterten die Ergebnisse zur Längengeneralisierung bei NLP-Aufgaben und entdeckten die Bedeutung von Positionseinbettungen für die Gewährleistung einer kausalen Generalisierung über die Länge und andere Dimensionen hinweg. Ihr leistungsstärkstes Modell hatte keine Positionskodierung, aber sie stellten auch fest, dass die Sinuskodierung in einigen Fällen gut funktionierte. Diese Axiom-Trainingsmethode kann auch auf ein schwierigeres Problem verallgemeinert werden, wie in Abbildung 5 dargestellt. Das heißt, auf der Grundlage von Prämissen, die Aussagen über statistische Unabhängigkeit enthalten, besteht das Ziel der Aufgabe darin, Korrelation von Kausalität zu unterscheiden. Die Lösung dieser Aufgabe erfordert die Kenntnis mehrerer Axiome, einschließlich d-Trennung und Markov-Eigenschaften. 
Das Team generierte synthetische Trainingsdaten mit der gleichen Methode wie oben und trainierte dann ein Modell. Es wurde festgestellt, dass der Transformer, der an einer Aufgabendemonstration mit 3-4 Variablen trainiert wurde, lernen konnte, Probleme mit 5 Variablen zu lösen Aufgaben. Und bei dieser Aufgabe ist das Modell genauer als größere LLMs wie GPT-4 und Gemini Pro. 
Das Team sagte: „Unsere Forschung liefert ein neues Paradigma für das Lehren von Modellen zum Erlernen des kausalen Denkens durch symbolische Demonstrationen von Axiomen, was wir als axiomatisches Training bezeichnen. Das Verfahren ist allgemein: so lange.“ Da ein Axiom im Format symbolischer Tupel ausgedrückt werden kann, kann es mit dieser Methode gelernt werden. Das obige ist der detaillierte Inhalt vonAxiomatisches Training ermöglicht es LLM, kausales Denken zu erlernen: Das 67-Millionen-Parameter-Modell ist vergleichbar mit der Billionen-Parameter-Ebene GPT-4. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Axiomatisches Training ermöglicht es LLM, kausales Denken zu erlernen: Das 67-Millionen-Parameter-Modell ist vergleichbar mit der Billionen-Parameter-Ebene GPT-4
Axiomatisches Training ermöglicht es LLM, kausales Denken zu erlernen: Das 67-Millionen-Parameter-Modell ist vergleichbar mit der Billionen-Parameter-Ebene GPT-4

















 Von RLHF über DPO bis TDPO sind große Modellausrichtungsalgorithmen bereits auf „Token-Ebene'
Jun 24, 2024 pm 03:04 PM
Von RLHF über DPO bis TDPO sind große Modellausrichtungsalgorithmen bereits auf „Token-Ebene'
Jun 24, 2024 pm 03:04 PM
 Posthume Arbeit des OpenAI Super Alignment Teams: Zwei große Modelle spielen ein Spiel und die Ausgabe wird verständlicher
Jul 19, 2024 am 01:29 AM
Posthume Arbeit des OpenAI Super Alignment Teams: Zwei große Modelle spielen ein Spiel und die Ausgabe wird verständlicher
Jul 19, 2024 am 01:29 AM
 Die agentenlose Lösung von UIUC steht ganz oben auf der Liste der Open-Source-KI-Softwareentwickler und löst problemlos echte Programmierprobleme im SWE-Bench
Jul 17, 2024 pm 10:02 PM
Die agentenlose Lösung von UIUC steht ganz oben auf der Liste der Open-Source-KI-Softwareentwickler und löst problemlos echte Programmierprobleme im SWE-Bench
Jul 17, 2024 pm 10:02 PM
 Der Autor von ControlNet hat einen weiteren Hit! Der gesamte Prozess der Generierung eines Gemäldes aus einem Bild, der in zwei Tagen 1,4.000 Sterne verdient
Jul 17, 2024 am 01:56 AM
Der Autor von ControlNet hat einen weiteren Hit! Der gesamte Prozess der Generierung eines Gemäldes aus einem Bild, der in zwei Tagen 1,4.000 Sterne verdient
Jul 17, 2024 am 01:56 AM
 Unbegrenzte Videogenerierung, Planung und Entscheidungsfindung, erzwungene Verbreitung der nächsten Token-Vorhersage und vollständige Sequenzverbreitung
Jul 23, 2024 pm 02:05 PM
Unbegrenzte Videogenerierung, Planung und Entscheidungsfindung, erzwungene Verbreitung der nächsten Token-Vorhersage und vollständige Sequenzverbreitung
Jul 23, 2024 pm 02:05 PM
 Ein bedeutender Durchbruch in der Riemann-Hypothese! Tao Zhexuan empfiehlt dringend neue Arbeiten vom MIT und Oxford, und der 37-jährige Fields-Medaillengewinner nahm daran teil
Aug 05, 2024 pm 03:32 PM
Ein bedeutender Durchbruch in der Riemann-Hypothese! Tao Zhexuan empfiehlt dringend neue Arbeiten vom MIT und Oxford, und der 37-jährige Fields-Medaillengewinner nahm daran teil
Aug 05, 2024 pm 03:32 PM
 arXiv-Artikel können als „Barrage' gepostet werden, die Diskussionsplattform von Stanford alphaXiv ist online, LeCun gefällt es
Aug 01, 2024 pm 05:18 PM
arXiv-Artikel können als „Barrage' gepostet werden, die Diskussionsplattform von Stanford alphaXiv ist online, LeCun gefällt es
Aug 01, 2024 pm 05:18 PM
 Axiomatisches Training ermöglicht es LLM, kausales Denken zu erlernen: Das 67-Millionen-Parameter-Modell ist vergleichbar mit der Billionen-Parameter-Ebene GPT-4
Jul 17, 2024 am 10:14 AM
Axiomatisches Training ermöglicht es LLM, kausales Denken zu erlernen: Das 67-Millionen-Parameter-Modell ist vergleichbar mit der Billionen-Parameter-Ebene GPT-4
Jul 17, 2024 am 10:14 AM






