
Haben Sie sich jemals gefragt, warum Casinos immer zu gewinnen scheinen? In „Beating the Odds: The Mathematics Behind Casino Profits“ erforschen wir die einfache Mathematik und clevere Strategien, die dafür sorgen, dass Casinos auf lange Sicht Geld verdienen. Anhand leicht verständlicher Beispiele und Monte-Carlo-Simulationen enthüllen wir die Geheimnisse hinter dem Hausvorteil. Machen Sie sich bereit zu entdecken, wie Casinos die Chancen zu ihren Gunsten wenden!
Der Hausvorteil ist ein grundlegendes Konzept in der Welt der Casinos. Es stellt den durchschnittlichen Gewinn dar, den das Casino mit jeder von Spielern platzierten Wette erwartet. Im Wesentlichen ist es der Prozentsatz jedes Einsatzes, den das Casino langfristig behält.
Der Hausvorteil besteht, weil Casinos gewonnene Wetten nicht entsprechend den „wahren Gewinnchancen“ des Spiels auszahlen. Echte Quoten geben die tatsächliche Wahrscheinlichkeit des Eintretens eines Ereignisses an. Durch die Auszahlung zu etwas niedrigeren Quoten stellen Casinos sicher, dass sie im Laufe der Zeit einen Gewinn erzielen.
Der Hausvorteil (HE) ist definiert als der Casino-Gewinn, ausgedrückt als Prozentsatz des ursprünglichen Einsatzes des Spielers.
** Europäisches Roulette ** hat nur eine grüne Null, also insgesamt 37 Zahlen. Wenn ein Spieler 1 $ auf Rot setzt, hat er eine Chance von 18/37, 1 $ zu gewinnen, und eine Chance von 19/37, 1 $ zu verlieren. Der erwartete Wert ist:
Erwarteter Wert=( 1 × 18/37 )+( −1 × 19/37 )= 18/37 − 19/37 = −1/37 ≈ −2,7 %
Daher beträgt der Hausvorteil (HE) beim Europäischen Roulette etwa 2,7 %.
Lassen Sie uns das Spiel zu unserem eigenen machen, um es besser zu verstehen, ein einfaches Würfelspiel.
import random
def roll_dice():
roll = random.randint(1, 100)
if roll == 100:
print(roll, 'You rolled a 100 and lost. Better luck next time!')
return False
elif roll <= 50:
print(roll, 'You rolled between 1 and 50 and lost.')
return False
else:
print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
return True
In diesem Spiel:
Der Spieler hat eine Chance von 1/100 zu verlieren, wenn der Wurf 100 ist.
Der Spieler hat eine 50/100-Chance zu verlieren, wenn der Wurf zwischen 1 und 50 liegt.
Der Spieler hat eine Gewinnchance von 49/100, wenn der Wurf zwischen 51 und 99 liegt.
Erwarteter Wert =(1× 49/100) + ( −1× 51/100) = 49/100 − 51/100 = −2/100 ≈ −2%
Daher beträgt der Hausvorteil 2 %.
Monte-Carlo-Simulationen sind ein leistungsstarkes Werkzeug zum Verständnis und zur Vorhersage komplexer Systeme, indem zahlreiche Simulationen eines Prozesses durchgeführt und die Ergebnisse beobachtet werden. Im Kontext von Casinos können Monte-Carlo-Simulationen verschiedene Wettszenarien modellieren, um zu zeigen, wie der Hausvorteil die langfristige Rentabilität gewährleistet. Lassen Sie uns untersuchen, wie Monte-Carlo-Simulationen funktionieren und wie sie auf ein einfaches Casinospiel angewendet werden können.
Bei einer Monte-Carlo-Simulation werden Zufallsvariablen generiert, um einen Prozess mehrmals zu simulieren, und die Ergebnisse analysiert. Indem wir Tausende oder sogar Millionen von Iterationen durchführen, können wir eine Verteilung möglicher Ergebnisse erhalten und Erkenntnisse über die Wahrscheinlichkeit verschiedener Ereignisse gewinnen.
Wir werden eine Monte-Carlo-Simulation verwenden, um das zuvor besprochene Würfelspiel zu modellieren. Dies wird uns helfen zu verstehen, wie sich der Hausvorteil im Laufe der Zeit auf die Rentabilität des Spiels auswirkt.
`def monte_carlo_simulation(trials):
wins = 0
losses = 0
for _ in range(trials):
if roll_dice():
wins += 1
else:
losses += 1
win_percentage = (wins / trials) * 100
loss_percentage = (losses / trials) * 100
houseEdge= loss_percentage-win_percentage
print(f"After {trials} trials:")
print(f"Win percentage: {win_percentage:.2f}%")
print(f"Loss percentage: {loss_percentage:.2f}%")
print(f"House Edge: {houseEdge:.2f}%")
# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`
In dieser Simulation führen wir das Würfelspiel 10.000.000 Mal durch, um die Gewinn- und Verlustprozentsätze zu beobachten. Angesichts des zuvor berechneten Hausvorteils (2 %) erwarten wir, dass der Verlustprozentsatz etwas höher ausfällt als der Gewinnprozentsatz.
Nachdem Sie die Simulation ausgeführt haben, sehen Sie möglicherweise Ergebnisse wie:
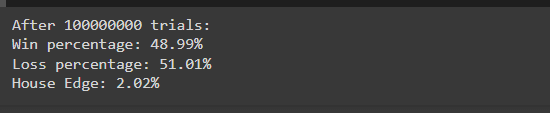
Diese Ergebnisse stimmen eng mit den theoretischen Wahrscheinlichkeiten überein (49 % Gewinn, 51 % Verlust) und zeigen, wie sich der Hausvorteil über eine große Anzahl von Versuchen hinweg manifestiert. Das leichte Ungleichgewicht sichert langfristig die Rentabilität des Casinos.
Monte-Carlo-Simulationen eignen sich hervorragend zur Modellierung und Vorhersage von Ergebnissen durch wiederholte Zufallsstichproben. Im Zusammenhang mit Glücksspielen können wir Monte-Carlo-Simulationen verwenden, um die möglichen Ergebnisse verschiedener Wettstrategien zu verstehen.
Wir simulieren einen einzelnen Wettenden, der in jeder Runde den gleichen Anfangseinsatz setzt, und beobachten, wie sich sein Kontowert über eine bestimmte Anzahl von Einsätzen entwickelt.
So können wir die Wettreise mit Matplotlib simulieren und visualisieren:
def bettor_simulation(funds, initial_wager, wager_count):
value = funds
wager = initial_wager
# Lists to store wager count and account value
wX = []
vY = []
current_wager = 1
while current_wager <= wager_count:
if roll_dice():
value += wager
else:
value -= wager
wX.append(current_wager)
vY.append(value)
current_wager += 1
return wX, vY
# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000
# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)
# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()
# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')
plt.legend()
plt.show()
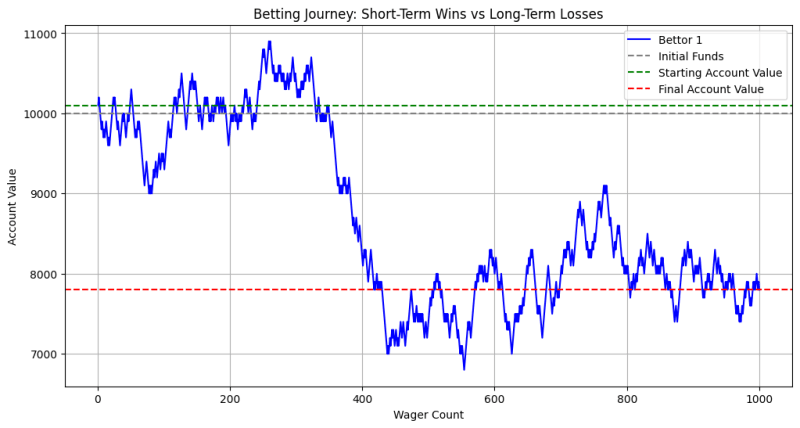
Diese Grafik veranschaulicht, wie der Kontowert eines Wettenden im Laufe der Zeit aufgrund von Gewinnen und Verlusten schwanken kann. Anfangs kann es Gewinnperioden geben (grüne Linie über dem Startwert), aber mit zunehmender Anzahl an Einsätzen wird die kumulative Wirkung des Hausvorteils deutlich. Letztendlich sinkt der Kontowert des Wettenden tendenziell in Richtung oder unter das ursprüngliche Guthaben (graue Linie), was auf langfristige Verluste hindeutet.
Wenn man die Mathematik hinter den Casinogewinnen versteht, erkennt man durch das Konzept des Hausvorteils in jedem Spiel einen klaren Vorteil für das Haus. Trotz gelegentlicher Gewinne sorgt die in Casinospielen eingebaute Wahrscheinlichkeit dafür, dass die meisten Spieler mit der Zeit Geld verlieren. Monte-Carlo-Simulationen veranschaulichen diese Dynamik anschaulich und zeigen, wie selbst kurzfristige Gewinne aufgrund des statistischen Vorteils des Casinos langfristige Verluste überdecken können. Dieser Einblick in die mathematische Sicherheit der Casino-Rentabilität unterstreicht die Bedeutung einer fundierten Entscheidungsfindung und verantwortungsvoller Spielpraktiken.
Als nächstes könnten wir zusätzliche Visualisierungen oder Variationen untersuchen, z. B. den Vergleich verschiedener Wettstrategien oder die Analyse der Auswirkungen unterschiedlicher Anfangseinsätze auf die Ergebnisse des Wettenden.
Bleiben Sie in Verbindung:
GitHub: ezhillragesh
Twitter: ezhillragesh
Website: ragesh.me
Zögern Sie nicht, Ihre Gedanken mitzuteilen, Fragen zu stellen und zur Diskussion beizutragen.
Viel Spaß beim Codieren!
Das obige ist der detaillierte Inhalt vonDen Chancen trotzen: Die Mathematik hinter Casino-Gewinnen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So entsperren Sie die Passwortsperre auf Ihrem Apple-Telefon, wenn Sie sie vergessen
So entsperren Sie die Passwortsperre auf Ihrem Apple-Telefon, wenn Sie sie vergessen
 So beheben Sie einen Webstorm-Absturz
So beheben Sie einen Webstorm-Absturz
 Was sind Endgeräte?
Was sind Endgeräte?
 Einführung in die Klassifizierung von Linux-Systemen
Einführung in die Klassifizierung von Linux-Systemen
 Was bedeutet PS-Maske?
Was bedeutet PS-Maske?
 So verwenden Sie die Groupby-Funktion
So verwenden Sie die Groupby-Funktion
 So verwenden Sie aspose
So verwenden Sie aspose
 Die Verwendung von „declare' in Oracle
Die Verwendung von „declare' in Oracle




