
Originaltitel: „Diese 3 Excel-Finanzfunktionen werden wieder einmal unterbewertet!“ 》
Der Autor dieses Artikels: Xiaohua
Der Herausgeber dieses Artikels: Yanlan
Kürzlich stieß Xiaohua auf eine interessante Frage, die aus der Seele eines alten Freundes kam:
Wie bezahle ich monatliche und private Renten? Treffen Sie eine Wahl für die Finanzierung einer Versicherung auf Gegenseitigkeit?
Die grundlegenden Informationen dieser beiden Finanzprodukte lauten wie folgt:
Monatliche Rente:
Zahlen Sie 1.000 Yuan pro Monat, der jährliche Zinssatz beträgt 3 %, die Laufzeit beträgt 2 Jahre, und der Kapitalbetrag und die Zinsen können betragen bei Fälligkeit auf einmal abgezogen.
Versicherungsfinanzierung auf Gegenseitigkeit:
Zahlen Sie jeden Monat einen Kapitalbetrag von 1.000 Yuan. Der monatliche Kapitalbetrag wird mit 10 % Zinsen und einer Laufzeit von 2 Jahren berechnet. Es nehmen 24 Personen an demselben Produkt teil. Jeden Monat muss eine Person den gesamten Kapitalbetrag und die von den anderen gezahlten Zinsen erhalten. Im nächsten Monat nach Erhalt der Zahlung muss eine Person 100 Yuan pro Monat zahlen.
Wie vergleicht man die Vor- und Nachteile dieser beiden Finanzprodukte?
Wir können dieses Problem anhand der Endwertmethode, der Renditemethode und der IRR-Methode betrachten und nebenbei einige Verwendungen von Finanzfunktionen mit Ihnen teilen.
Die Methode der Endwertanalyse besteht darin, den Endwert des Nettonutzens des Plans (Projekts) nach Bestimmung des Basisjahres, des Umwandlungszinssatzes und des Cashflows zu berechnen. Je höher der Endwert, desto größer ist die Wirtschaftlichkeit der Lösung.
Wie viel Kapital und Zinsen können nach Fälligkeit der Rente in gleicher Höhe erhalten werden? Dieses Problem kann mit der Endwertfunktion FV berechnet werden.

Renten-Zukunftswertformel:
=-FV(B3/12,C3,A3)

Es ist ersichtlich, dass, wenn jeden Monat eine Rente von 1.000 Yuan gezahlt wird, die Der Zinssatz wird mit 3 % berechnet. Nach 2 Jahren werden insgesamt 24.703 Yuan an Kapital und Zinsen erhalten.
Der Endwert von „Mutual Insurance Finance“ (vorausgesetzt, es erfolgt keine fortlaufende Investition) hängt von der Reihenfolge ab, in der Kapital und Zinsen abgehoben werden. Je später die Auszahlung erfolgt, desto höher ist das Einkommen. Der Endwert wird wie folgt berechnet:
=S2*U2+S2*T2*(V2-1)-S2*T2*(U2-V2)

Aus Sicht der Endwertmethode wenn Sie den Erhalt sicherstellen können. Wenn der Zahlungszeitraum nach 16 Perioden liegt, ist das Einkommen von „Mutual Insurance Finance“ höher als die monatliche Rente. Wenn der Empfangszeitraum früher als 16 Perioden liegt, ist das Einkommen von „Mutual Insurance Finance“ geringer als die monatliche Rente.
Die Terminal-Value-Methode eignet sich für Investitionsvorhaben mit vergleichbarem Investitionsumfang.
Als ich meinem alten Freund diese vorläufige Schlussfolgerung erzählte, fragte er ungläubig:
Warum beträgt der Nominalzinssatz von „Mutual Insurance Finance“ 10 %? /3 des Einkommens der Teilnehmer höher ist als das der monatlichen Rente, die eine Rendite von nur 3 % hat?
Hier geht es um die Berechnung der Rentabilität.
Die Renditemethode ist eine Investitionsentscheidungsmethode, die die durchschnittliche jährliche Nettorendite eines Investitionsprojekts mit den Kapitalkosten der Investition vergleicht, um festzustellen, ob die Investition wünschenswert ist, und dann den Investitionsplan auswählt die höchste Rendite unter den verfügbaren Anlageplänen.
Natürlich entspricht die monatliche Rentenrendite dem Nominalzinssatz, der bei 3 % liegt.
Wie hoch ist also die Rendite für jeden Zahlungszeitraum von „Mutual Insurance Finance“?
Wir können die Funktion RATE zur Berechnung verwenden.

Die Rendite von „Mutual Insurance Finance“ wird wie folgt berechnet:
=RATE(U2-S2,0,W2,0)*12

Aus der Rate von Renditemethode: Obwohl der Nominalzinssatz der „Mutual Insurance Finance“ bis zu 10 % beträgt, kann die Rendite tatsächlich nur dann 3 % erreichen, wenn die Teilnehmer Kapital und Zinsen nach 16 Perioden erhalten. Die Rendite ist niedriger als das Einkommen der monatlichen Rente. Die Rate beträgt 3 %. Es ist ersichtlich, dass die Rendite der „gegenseitigen Versicherungsfinanzierung“ immer noch hoch ist.
Allerdings ist es unfair zu beurteilen, dass die Erträge der „Versicherungsfinanzierung auf Gegenseitigkeit“ nicht so gut sind wie die der monatlichen Rente „Finanzen“ kann einen Kapitalzufluss im Voraus realisieren. Wenn dieser Teil der Mittel wieder für Investitionen verwendet wird, wird die „gegenseitige Versicherungsfinanzierung“ erheblich verbessert.
Im Finanzmanagement wird häufig der Zeitwert verwendet, um diesen Unterschied zu erklären. Der interne Zinsfuß (IRR) und der Nettobarwert (NPV) können zur Messung der dynamischen Rendite einer Investition verwendet werden.
Unten wählen wir NPV, um diese beiden Finanzprodukte zu vergleichen. Die IRR-Vergleichsmethode ist in diesem Fall nicht anwendbar.

Bevor wir den Nettobarwert berechnen, müssen wir die Cashflows der beiden Produkte in jeder Periode auflisten und dann die NPV-Funktion zur Berechnung verwenden.

Bayaran bulanan sebanyak 1,000 yuan untuk anuiti bulanan Selepas 24 pembayaran, prinsipal dan faedah sebanyak 24,703 yuan akan dipulihkan dalam satu jumlah sekaligus /12,B2:Y2)

"Mutual Insurance Finance" mempunyai beberapa kemungkinan tempoh pengeluaran, jadi apabila mengira IRR produk ini, kita perlu menggunakan jadual simulasi untuk mencapainya.
Pengiraan NPV "Mutual Insurance Finance":
❶ Dengan mengambil tempoh pengeluaran sebagai pembolehubah, aliran tunai setiap tempoh yang dikira berdasarkan pembolehubah disenaraikan.
Aliran tunai prinsipal, nombor positif menunjukkan pembayaran, dan nombor negatif menunjukkan pengeluaran.
=IF(E$4=$G$2,-$D$2*23,$D$2)
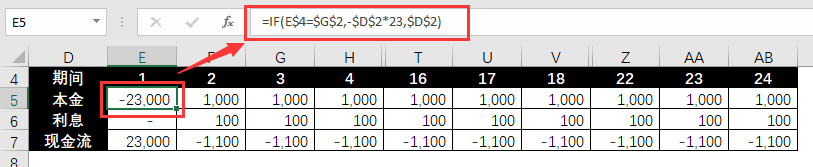
=IFS(E4
$G$2,$D$2*$E$2)

=NPV(H2/12,E7:AB7)
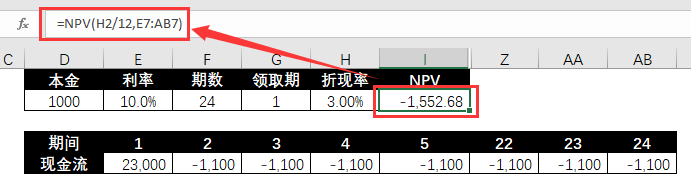
❸ Gunakan jadual simulasi untuk mengira NPV yang sepadan dengan tempoh pengekstrakan yang berbeza.
① Senaraikan nilai pembolehubah tempoh pengumpulan yang diperlukan dan pautkan nilai hasil yang sepadan dalam baris pertama.

② Pilih baris pautan, kawasan nilai berubah dan kawasan nilai hasil, dan ikuti langkah di bawah untuk melengkapkan operasi simulasi.

Hasil pengiraan simulasi adalah seperti berikut:

Dari perspektif NPV, pendapatan "kewangan insurans bersama" dan anuiti bulanan adalah setanding.
Di antara semua peserta yang terdahulu, pulangan perbandingan mereka bercampur-campur Ini kerana peserta yang mempunyai tempoh tuntutan yang lebih awal boleh memperoleh aliran masuk tunai dengan lebih pantas untuk pelaburan bergulir, yang pada tahap tertentu melindung nilai terhadap kehilangan kadar faedah yang tinggi. Ringkasnya, apabila
adalah mustahil untuk merealisasikan pelaburan bergulir atau mengejar kepastian, anda harus memilih anuiti bulanan untuk pelaburan Produk ini mempunyai pendapatan pelaburan yang stabil dan pendapatan statik purata yang lebih tinggi. Jika anda
mengejar pulangan dinamik yang lebih tinggi atau dapat membuat pelaburan sekunder selepas mengeluarkan prinsipal dan faedah, anda harus memilih "Mutual Insurance Finance" untuk pengurusan kewangan yang kedua mempunyai peluang untuk mencapai nilai semasa bersih dan pulangan statik yang lebih tinggi.
Di atas adalah lanjutan Xiaohua daripada masalah pemilihan produk kewangan Ia menerangkan penggunaan beberapa formula dan fungsi kewangan Excel, termasuk:
❶ fungsi FV dan fungsi RATE
❷ Fungsi NPV
❸ Jadual simulasi
. Jika anda seorang akauntan kewangan, atau mempunyai keperluan atau minat dalam pengiraan kewangan, formula dan kes praktikal ini akan membantu anda.
Das obige ist der detaillierte Inhalt vonLösen Sie komplexe Finanzberechnungen mit 3 Excel-Finanzfunktionen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Vergleichen Sie die Ähnlichkeiten und Unterschiede zwischen zwei Datenspalten in Excel
Vergleichen Sie die Ähnlichkeiten und Unterschiede zwischen zwei Datenspalten in Excel
 Excel-Duplikatfilter-Farbmarkierung
Excel-Duplikatfilter-Farbmarkierung
 So kopieren Sie eine Excel-Tabelle, um sie auf die gleiche Größe wie das Original zu bringen
So kopieren Sie eine Excel-Tabelle, um sie auf die gleiche Größe wie das Original zu bringen
 Excel-Tabellen-Schrägstrich in zwei Teile geteilt
Excel-Tabellen-Schrägstrich in zwei Teile geteilt
 Die diagonale Kopfzeile von Excel ist zweigeteilt
Die diagonale Kopfzeile von Excel ist zweigeteilt
 Absolute Referenzeingabemethode
Absolute Referenzeingabemethode
 Java-Export Excel
Java-Export Excel
 Der Excel-Eingabewert ist unzulässig
Der Excel-Eingabewert ist unzulässig




