 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 timeit.repeat – mit Wiederholungen spielen, um Muster zu verstehen
timeit.repeat – mit Wiederholungen spielen, um Muster zu verstehen
timeit.repeat – mit Wiederholungen spielen, um Muster zu verstehen
1. Das Problem
Im Laufe Ihrer Karriere als Softwareentwickler stoßen Sie möglicherweise auf einen Codeabschnitt, der eine schlechte Leistung erbringt und viel länger als akzeptabel dauert. Erschwerend kommt hinzu, dass die Leistung bei mehreren Ausführungen inkonsistent und recht schwankend ist.
Zu diesem Zeitpunkt müssten Sie akzeptieren, dass bei der Softwareleistung eine Menge Nichtdeterminismus im Spiel ist. Die Daten können innerhalb eines Fensters verteilt sein und folgen manchmal einer Normalverteilung. In anderen Fällen kann es unregelmäßig und ohne erkennbare Muster sein.
2. Der Ansatz
Hier kommt Benchmarking ins Spiel. Den Code fünfmal auszuführen ist gut, aber am Ende des Tages haben Sie nur fünf Datenpunkte, wobei jedem Datenpunkt zu viel Wert beigemessen wird. Wir benötigen eine viel größere Anzahl von Wiederholungen desselben Codeblocks, um ein Muster zu erkennen.
3. Die Frage
Wie viele Datenpunkte sollte man haben? Es wurde schon viel darüber geschrieben, und einer der Artikel, die ich behandelt habe
Eine strenge Leistungsbewertung erfordert die Erstellung von Benchmarks,
mehrfach ausgeführt und gemessen, um mit Zufällen umzugehen
Variation in den Ausführungszeiten. Forscher sollten Maßnahmen bereitstellen
Abweichungen bei der Ergebnisberichterstattung.
Kalibera, T. & Jones, R. (2013). Strenges Benchmarking in angemessener Zeit. Tagungsband des International Symposium on Memory Management 2013. https://doi.org/10.1145/2491894.2464160
Bei der Leistungsmessung möchten wir möglicherweise die CPU-, Speicher- oder Festplattennutzung messen, um ein umfassenderes Bild der Leistung zu erhalten. Normalerweise ist es am besten, mit etwas Einfachem zu beginnen, wie zum Beispiel der verstrichenen Zeit, da es einfacher zu visualisieren ist. Eine CPU-Auslastung von 17 % sagt uns nicht viel. Was soll es sein? 20 % oder 5? Die CPU-Auslastung gehört nicht zu den natürlichen Arten, wie Menschen Leistung wahrnehmen.
4. Das Experiment
Ich werde die timeit.repeat-Methode von Python verwenden, um einen einfachen Codeausführungsblock zu wiederholen. Der Codeblock multipliziert einfach Zahlen von 1 bis 2000.
from functools import reduce reduce((lambda x, y: x * y), range(1, 2000))
Dies ist die Methodensignatur
(function) def repeat(
stmt: _Stmt = "pass",
setup: _Stmt = "pass",
timer: _Timer = ...,
repeat: int = 5,
number: int = 1000000,
globals: dict[str, Any] | None = None
) -> list[float]
Was sind Wiederholung und Zahl?
Beginnen wir mit der Zahl. Wenn der Codeblock zu klein ist, wird er so schnell beendet, dass Sie nichts mehr messen können. Dieses Argument gibt an, wie oft der stmt ausgeführt werden muss. Sie können dies als den neuen Codeblock betrachten. Der zurückgegebene Float gilt für die Ausführungszeit der StMT-X-Nummer.
In unserem Fall behalten wir die Zahl 1000 bei, da die Multiplikation bis 2000 teuer ist.
Als nächstes wiederholen Sie den Vorgang. Dies gibt die Anzahl der Wiederholungen bzw. die Häufigkeit an, mit der der obige Block ausgeführt werden muss. Wenn die Wiederholung 5 ist, gibt die Liste[float] 5 Elemente zurück.
Beginnen wir mit der Erstellung eines einfachen Ausführungsblocks
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
Wir wollen es in verschiedenen Wiederholungswerten ausführen
repeat_values = [5, 20, 100, 500, 3000, 10000]
Der Code ist ziemlich einfach und unkompliziert
5. Erkundung der Ergebnisse
Jetzt kommen wir zum wichtigsten Teil des Experiments – nämlich der Interpretation der Daten. Bitte beachten Sie, dass verschiedene Personen die Frage unterschiedlich interpretieren können und es nicht die eine einzige richtige Antwort gibt.
Ihre Definition einer richtigen Antwort hängt stark davon ab, was Sie erreichen möchten. Sind Sie besorgt über den Leistungsabfall von 95 % Ihrer Benutzer? Oder machen Sie sich Sorgen über einen Leistungsabfall bei den letzten 5 % Ihrer Benutzer, die recht lautstark sind?
5.1. Statistiken zur Ausführungszeitanalyse für mehrere Wiederholungswerte
Wie wir sehen können, sind die Mindest- und Höchstzeit verrückt. Es zeigt, wie ein Datenpunkt ausreichen kann, um den Mittelwert zu ändern. Das Schlimmste daran ist, dass hohe Mindest- und Höchstwerte für unterschiedliche Wiederholungswerte gelten. Es gibt keine Korrelation und es zeigt lediglich die Macht von Ausreißern.
Als nächstes gehen wir zum Median über und stellen fest, dass der Median sinkt, wenn wir die Anzahl der Wiederholungen erhöhen, bis auf 20. Was kann das erklären? Es zeigt nur, dass eine geringere Anzahl von Wiederholungen bedeutet, dass wir nicht unbedingt den vollen Umfang möglicher Werte erhalten.
Umstellung auf den abgeschnittenen Mittelwert, bei dem die niedrigsten 2,5 % und die höchsten 2,5 % abgeschnitten werden. Dies ist nützlich, wenn Sie sich nicht um Ausreißerbenutzer kümmern und sich auf die Leistung der mittleren 95 % Ihrer Benutzer konzentrieren möchten.
Vorsicht: Der Versuch, die Leistung der mittleren 95 % der Benutzer zu verbessern, birgt die Möglichkeit, dass die Leistung der aussergewöhnlichen 5 % der Benutzer beeinträchtigt wird.

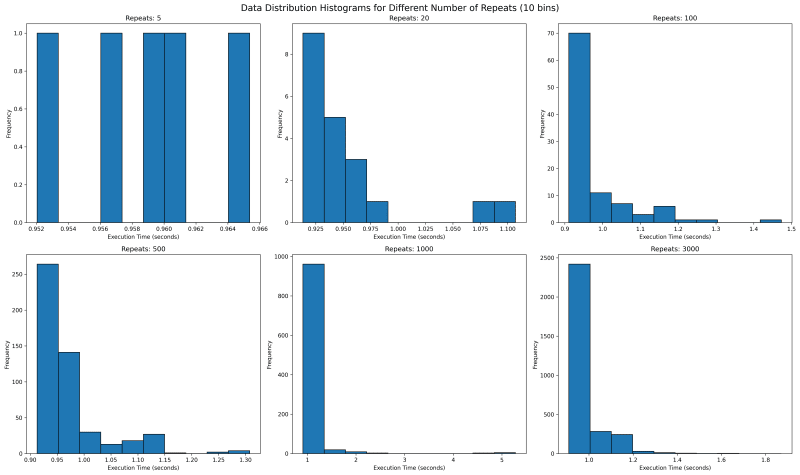
5.2. Execution Time Distribution for multiple values of repeat
Next we want to see where all the data lies. We would use histogram with bin of 10 to see where the data falls. With repetitions of 5 we see that they are mostly equally spaced. This is not one usually expects as sampled data should follow a normal looking distribution.
In our case the value is bounded on the lower side and unbounded on the upper side, since it will take more than 0 seconds to run any code, but there is no upper time limit. This means our distribution should look like a normal distribution with a long right tail.
Going forward with higher values of repeat, we see a tail emerging on the right. I would expect with higher number of repeat, there would be a single histogram bar, which is tall enough that outliers are overshadowed.
5.3. Execution Time Distribution for values 1000 and 3000
How about we look at larger values of repeat to get a sense? We see something unusual. With 1000 repeats, there are a lot of outliers past 1.8 and it looks a lot more tighter. The one on the right with 3000 repeat only goes upto 1.8 and has most of its data clustered around two peaks.
What can it mean? It can mean a lot of things including the fact that sometimes maybe the data gets cached and at times it does not. It can point to many other side effects of your code, which you might have never thought of. With the kind of distribution of both 1000 and 3000 repeats, I feel the TM95 for 3000 repeat is the most accurate value.

6. Appendix
6.1. Code
import timeit
import matplotlib.pyplot as plt
import json
import os
import statistics
import numpy as np
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
def save_result(result, repeats):
filename = f'execution_time_results_{repeats}.json'
with open(filename, 'w') as f:
json.dump(result, f)
def load_result(repeats):
filename = f'execution_time_results_{repeats}.json'
if os.path.exists(filename):
with open(filename, 'r') as f:
return json.load(f)
return None
def truncated_mean(data, percentile=95):
data = np.array(data)
lower_bound = np.percentile(data, (100 - percentile) / 2)
upper_bound = np.percentile(data, 100 - (100 - percentile) / 2)
return np.mean(data[(data >= lower_bound) & (data <= upper_bound)])
# List of number_of_repeats to test
repeat_values = [5, 20, 100, 500, 1000, 3000]
# Run experiments and collect results
results = []
for repeats in repeat_values:
result = load_result(repeats)
if result is None:
print(f"Running experiment for {repeats} repeats...")
try:
result = run_experiment(repeats)
save_result(result, repeats)
print(f"Experiment for {repeats} repeats completed and saved.")
except KeyboardInterrupt:
print(f"\nExperiment for {repeats} repeats interrupted.")
continue
else:
print(f"Loaded existing results for {repeats} repeats.")
# Print time taken per repetition
avg_time = statistics.mean(result)
print(f"Average time per repetition for {repeats} repeats: {avg_time:.6f} seconds")
results.append(result)
trunc_means = [truncated_mean(r) for r in results]
medians = [np.median(r) for r in results]
mins = [np.min(r) for r in results]
maxs = [np.max(r) for r in results]
# Create subplots
fig, axs = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Execution Time Analysis for Different Number of Repeats', fontsize=16)
metrics = [
('Truncated Mean (95%)', trunc_means),
('Median', medians),
('Min', mins),
('Max', maxs)
]
for (title, data), ax in zip(metrics, axs.flatten()):
ax.plot(repeat_values, data, marker='o')
ax.set_title(title)
ax.set_xlabel('Number of Repeats')
ax.set_ylabel('Execution Time (seconds)')
ax.set_xscale('log')
ax.grid(True, which="both", ls="-", alpha=0.2)
# Set x-ticks and labels for each data point
ax.set_xticks(repeat_values)
ax.set_xticklabels(repeat_values)
# Rotate x-axis labels for better readability
ax.tick_params(axis='x', rotation=45)
plt.tight_layout()
# Save the plot to a file
plt.savefig('execution_time_analysis.png', dpi=300, bbox_inches='tight')
print("Plot saved as 'execution_time_analysis.png'")
# Create histograms for data distribution with 10 bins
fig, axs = plt.subplots(2, 3, figsize=(20, 12))
fig.suptitle('Data Distribution Histograms for Different Number of Repeats (10 bins)', fontsize=16)
for repeat, result, ax in zip(repeat_values, results, axs.flatten()):
ax.hist(result, bins=10, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the histograms to a file
plt.savefig('data_distribution_histograms_10bins.png', dpi=300, bbox_inches='tight')
print("Histograms saved as 'data_distribution_histograms_10bins.png'")
# Create histograms for 1000 and 3000 repeats with 30 bins
fig, axs = plt.subplots(1, 2, figsize=(15, 6))
fig.suptitle('Data Distribution Histograms for 1000 and 3000 Repeats (30 bins)', fontsize=16)
for repeat, result, ax in zip([1000, 3000], results[-2:], axs):
ax.hist(result, bins=100, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the detailed histograms to a file
plt.savefig('data_distribution_histograms_detailed.png', dpi=300, bbox_inches='tight')
print("Detailed histograms saved as 'data_distribution_histograms_detailed.png'")
plt.show()
Das obige ist der detaillierte Inhalt vontimeit.repeat – mit Wiederholungen spielen, um Muster zu verstehen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 So verwenden Sie Python, um die ZiPF -Verteilung einer Textdatei zu finden
Mar 05, 2025 am 09:58 AM
So verwenden Sie Python, um die ZiPF -Verteilung einer Textdatei zu finden
Mar 05, 2025 am 09:58 AM
So verwenden Sie Python, um die ZiPF -Verteilung einer Textdatei zu finden
 So herunterladen Sie Dateien in Python
Mar 01, 2025 am 10:03 AM
So herunterladen Sie Dateien in Python
Mar 01, 2025 am 10:03 AM
So herunterladen Sie Dateien in Python
 Wie benutze ich eine schöne Suppe, um HTML zu analysieren?
Mar 10, 2025 pm 06:54 PM
Wie benutze ich eine schöne Suppe, um HTML zu analysieren?
Mar 10, 2025 pm 06:54 PM
Wie benutze ich eine schöne Suppe, um HTML zu analysieren?
 Wie man mit PDF -Dokumenten mit Python arbeitet
Mar 02, 2025 am 09:54 AM
Wie man mit PDF -Dokumenten mit Python arbeitet
Mar 02, 2025 am 09:54 AM
Wie man mit PDF -Dokumenten mit Python arbeitet
 Wie kann man mit Redis in Django -Anwendungen zwischenstrichen
Mar 02, 2025 am 10:10 AM
Wie kann man mit Redis in Django -Anwendungen zwischenstrichen
Mar 02, 2025 am 10:10 AM
Wie kann man mit Redis in Django -Anwendungen zwischenstrichen
 Einführung des natürlichen Sprach -Toolkits (NLTK)
Mar 01, 2025 am 10:05 AM
Einführung des natürlichen Sprach -Toolkits (NLTK)
Mar 01, 2025 am 10:05 AM
Einführung des natürlichen Sprach -Toolkits (NLTK)
 Wie führe ich ein tiefes Lernen mit Tensorflow oder Pytorch durch?
Mar 10, 2025 pm 06:52 PM
Wie führe ich ein tiefes Lernen mit Tensorflow oder Pytorch durch?
Mar 10, 2025 pm 06:52 PM
Wie führe ich ein tiefes Lernen mit Tensorflow oder Pytorch durch?






