
Das Problem verbundener Kreise besteht darin, zu bestimmen, ob alle Kreise in einer zweidimensionalen Ebene verbunden sind. Dieses Problem kann mithilfe einer Tiefendurchquerung gelöst werden. Der DFS-Algorithmus hat viele Anwendungen. In diesem Abschnitt wird der DFS-Algorithmus angewendet, um das Problem der verbundenen Kreise zu lösen.
Bei dem Problem verbundener Kreise bestimmen Sie, ob alle Kreise in einer zweidimensionalen Ebene verbunden sind. Wenn alle Kreise verbunden sind, werden sie als gefüllte Kreise dargestellt, wie in Abbildung unten (a) dargestellt. Andernfalls werden sie nicht ausgefüllt, wie in Abbildung unten (b) dargestellt.
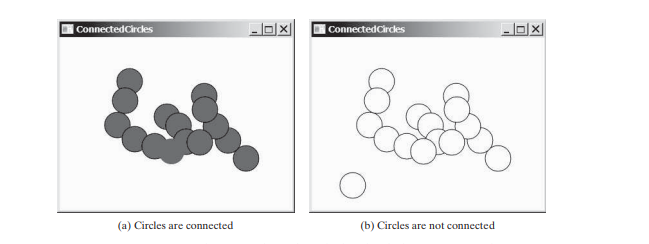
Wir werden ein Programm schreiben, mit dem der Benutzer einen Kreis erstellen kann, indem er mit der Maus in einen leeren Bereich klickt, der derzeit nicht von einem Kreis bedeckt ist. Wenn die Kreise hinzugefügt werden, werden die Kreise neu gezeichnet, wenn sie verbunden sind, oder wenn sie andernfalls ungefüllt sind.
Wir erstellen ein Diagramm, um das Problem zu modellieren. Jeder Kreis ist ein Scheitelpunkt im Diagramm. Zwei Kreise sind verbunden, wenn sie sich überlappen. Wir wenden das DFS im Diagramm an, und wenn bei der Tiefensuche alle Scheitelpunkte gefunden werden, ist das Diagramm verbunden.
Das Programm ist im folgenden Code angegeben.
import javafx.application.Application;
import javafx.geometry.Point2D;
import javafx.scene.Node;
import javafx.scene.Scene;
import javafx.scene.layout.Pane;
import javafx.scene.paint.Color;
import javafx.scene.shape.Circle;
import javafx.stage.Stage;
public class ConnectedCircles extends Application {
@Override // Override the start method in the Application class
public void start(Stage primaryStage) {
// Create a scene and place it in the stage
Scene scene = new Scene(new CirclePane(), 450, 350);
primaryStage.setTitle("ConnectedCircles"); // Set the stage title
primaryStage.setScene(scene); // Place the scene in the stage
primaryStage.show(); // Display the stage
}
public static void main(String[] args) {
Application.launch(args);
}
/** Pane for displaying circles */
class CirclePane extends Pane {
public CirclePane() {
this.setOnMouseClicked(e -> {
if (!isInsideACircle(new Point2D(e.getX(), e.getY()))) {
// Add a new circle
getChildren().add(new Circle(e.getX(), e.getY(), 20));
colorIfConnected();
}
});
}
/** Returns true if the point is inside an existing circle */
private boolean isInsideACircle(Point2D p) {
for (Node circle: this.getChildren())
if (circle.contains(p))
return true;
return false;
}
/** Color all circles if they are connected */
private void colorIfConnected() {
if (getChildren().size() == 0)
return; // No circles in the pane
// Build the edges
java.util.List<AbstractGraph.Edge> edges = new java.util.ArrayList<>();
for (int i = 0; i < getChildren().size(); i++)
for (int j = i + 1; j < getChildren().size(); j++)
if (overlaps((Circle)(getChildren().get(i)), (Circle)(getChildren().get(j)))) {
edges.add(new AbstractGraph.Edge(i, j));
edges.add(new AbstractGraph.Edge(j, i));
}
// Create a graph with circles as vertices
Graph<Node> graph = new UnweightedGraph<>((java.util.List<Node>)getChildren(), edges);
AbstractGraph<Node>.Tree tree = graph.dfs(0); // a DFS tree
boolean isAllCirclesConnected = getChildren().size() == tree.getNumberOfVerticesFound();
for (Node circle: getChildren()) {
if (isAllCirclesConnected) { // All circles are connected
((Circle)circle).setFill(Color.RED);
}
else {
((Circle)circle).setStroke(Color.BLACK);
((Circle)circle).setFill(Color.WHITE);
}
}
}
}
public static boolean overlaps(Circle circle1, Circle circle2) {
return new Point2D(circle1.getCenterX(), circle1.getCenterY()).distance(circle2.getCenterX(), circle2.getCenterY()) <= circle1.getRadius() + circle2.getRadius();
}
}
Die JavaFX-Klasse Circle enthält die Datenfelder x, y und radius, die die Mittelpunktposition und den Radius des Kreises angeben . Es definiert auch die Contains zum Testen, ob sich ein Punkt im Kreis befindet. Die Methode overlaps (Zeilen 76–80) prüft, ob sich zwei Kreise überlappen.
Wenn der Benutzer mit der Maus außerhalb eines vorhandenen Kreises klickt, wird ein neuer Kreis mit der Mitte des Mauspunkts erstellt und der Kreis dem Bereich hinzugefügt (Zeile 26).
Um festzustellen, ob die Kreise verbunden sind, erstellt das Programm einen Graphen (Zeilen 46–59). Die Kreise sind die Eckpunkte des Diagramms. Die Kanten werden in den Zeilen 49–55 konstruiert. Zwei Kreiseckpunkte sind verbunden, wenn sie sich überlappen (Zeile 51). Die DFS des Diagramms ergibt einen Baum (Zeile 60). getNumberOfVerticesFound() des Baums gibt die Anzahl der gesuchten Eckpunkte zurück. Wenn es gleich der Anzahl der Kreise ist, sind alle Kreise verbunden (Zeilen 61–62).
Das obige ist der detaillierte Inhalt vonFallstudie: Das Problem der verbundenen Kreise. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Einführung in Screenshot-Tastenkombinationen in Win10
Einführung in Screenshot-Tastenkombinationen in Win10
 So verwenden Sie Shuffle
So verwenden Sie Shuffle
 Linux View IP-Befehl
Linux View IP-Befehl
 Empfohlene benutzerfreundliche und formelle Software-Apps für Währungsspekulationen im Jahr 2024
Empfohlene benutzerfreundliche und formelle Software-Apps für Währungsspekulationen im Jahr 2024
 Aktuelles Ranking der digitalen Währungsbörsen
Aktuelles Ranking der digitalen Währungsbörsen
 HTML zum Erstellen von Webseiten
HTML zum Erstellen von Webseiten
 Was soll ich tun, wenn mein Laufwerk C rot wird?
Was soll ich tun, wenn mein Laufwerk C rot wird?
 So stellen Sie gelöschte Dateien auf dem Computer wieder her
So stellen Sie gelöschte Dateien auf dem Computer wieder her




