Baru-baru ini, buat pertama kalinya, kemajuan telah dicapai pada masalah matematik yang tidak dapat diselesaikan selama beberapa dekad.
Mendorong kemajuan ini ialah pelajar siswazah UCLA James Leng dan pelajar siswazah matematik MIT Ashwin Sah, dan penolong profesor Universiti Columbia Mehtaab Sawhney. Antaranya, James Leng belajar di bawah ahli matematik terkenal Terence Tao, dan Ashwin Sah belajar di bawah master matematik diskret Zhao Yufei.
Alamat kertas: https://arxiv.org/pdf/2402.17995
Untuk memahami kejayaan yang dicapai dalam penyelidikan ini, anda perlu bermula dengan janjang aritmetik.
Jumlah n sebutan pertama bagi jujukan aritmetik dipanggil siri aritmetik, juga dipanggil siri aritmetik. Pada tahun 1936, ahli matematik Paul Erdős dan Pál Turán menjangkakan bahawa jika set terdiri daripada pecahan bukan sifar integer (walaupun 0.00000001%), maka ia mesti mengandungi siri aritmetik yang panjang sewenang-wenangnya. Satu-satunya set yang boleh mengelakkan siri aritmetik ialah set yang mengandungi bahagian integer yang "boleh diabaikan". Sebagai contoh, set {2, 4, 8, 16, …}, di mana setiap nombor ialah dua kali nombor sebelumnya, dihamparkan di sepanjang paksi nombor tanpa janjang.
Pada tahun 1975, ahli matematik Endre Szemerédi membuktikan sangkaan ini. Kerja beliau menimbulkan pelbagai hala tuju penyelidikan yang masih diterokai oleh ahli matematik hari ini.
Ahli matematik menetapkan keputusan Szemerédi dalam konteks set nombor terhingga (semua integer dari 1 hingga beberapa nombor N). Berapa banyak kumpulan awal boleh digunakan dalam set sebelum tidak dapat tidak termasuk siri terlarang? Bagaimanakah perkadaran ini berubah apabila N berubah?
Sebagai contoh, biarkan N ialah 20, berapa banyakkah daripada 20 nombor ini yang boleh ditulis sambil masih mengelak siri yang panjangnya 5 atau lebih nombor? Jawapannya, ternyata, adalah 16% hingga 80% daripada kumpulan awal.
Szemerédi adalah orang pertama yang menunjukkan bahawa apabila N berkembang, pecahan ini mesti mengecut kepada sifar, dan ahli matematik telah mencuba untuk mengukur seberapa cepat perkara ini berlaku.
Tahun lepas, kerja pecah tanah oleh dua saintis komputer hampir menyelesaikan masalah siri tiga penggal, seperti {6, 11, 16}. Tetapi masalahnya menjadi lebih sukar apabila anda cuba mengelakkan siri aritmetik empat atau lebih istilah. Ini kerana siri yang lebih panjang mencerminkan struktur asas yang sukar didedahkan menggunakan kaedah matematik klasik.
Nombor x, y dan z dalam siri aritmetik tiga sebutan sentiasa memenuhi persamaan mudah x – 2y + z = 0 (mengambil siri {10, 20, 30} sebagai contoh: 10 – 2*(20) + 30 = 0), agak mudah untuk membuktikan sama ada set mengandungi nombor yang memenuhi syarat ini. Walaupun nombor dalam siri empat jangka juga mesti memenuhi persamaan yang lebih kompleks x^2 – 3y^2 + 3z^2 – w^2 = 0, siri dengan lima atau lebih sebutan mesti memenuhi persamaan yang lebih kompleks. Ini bermakna set yang mengandungi siri sedemikian akan mempamerkan corak yang lebih halus. Ia juga akan menjadi lebih sukar bagi ahli matematik untuk membuktikan sama ada corak sedemikian wujud.
Pada penghujung 1990-an, ahli matematik Timothy Gowers mencadangkan satu teori untuk mengatasi halangan ini. Beliau kemudiannya dianugerahkan Fields Medal, penghormatan tertinggi matematik, sebahagiannya untuk kerja ini. Pada tahun 2001, beliau menggunakan kaedahnya pada teorem Szemerédi, membuktikan had yang lebih baik pada saiz set maksimum, mengelakkan siri aritmetik untuk sebarang panjang tertentu.
Pada 2022, James Leng, ketika itu pelajar siswazah tahun kedua di UCLA, mula memahami teori Gowers. Dia tidak menganggap teorem Szemerédi. Sebaliknya, dia berharap dapat menjawab soalan mengenai pendekatan Gowers.
Namun, setelah berusaha bersungguh-sungguh untuk meneroka selama lebih setahun, dia tidak menemui apa-apa.
Sah dan Sawhney, yang telah memikirkan tentang isu berkaitan, mengetahui tentang kerja Leng dan sangat berminat malah Sawhney berkata: "Saya terkejut saya boleh berfikir seperti ini."
Sah dan Sawhney menyedari bahawa penyelidikan Leng mungkin membantu mereka membuat kemajuan selanjutnya dalam teorem Szemerédi. Dalam beberapa bulan, tiga ahli matematik muda memikirkan cara untuk mendapatkan had atas yang lebih baik pada saiz set tanpa siri pentterm. Mereka kemudian memanjangkan kerja mereka kepada siri panjang sewenang-wenangnya, menandakan kemajuan pertama dalam masalah itu dalam tempoh 23 tahun sejak bukti Gowers.
Biar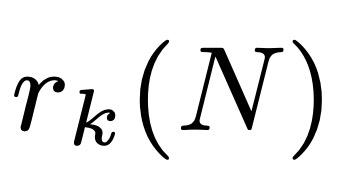 
menandakan 
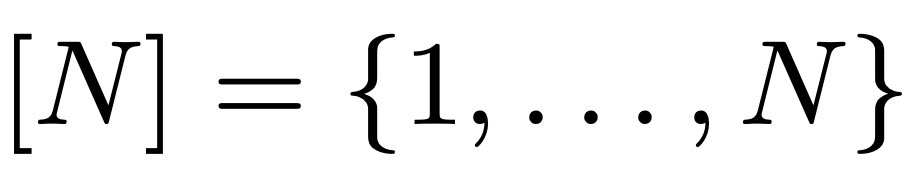, saiz subset terbesar siri aritmetik tanpa sebutan k. Leng, Sah dan Sawhney menunjukkan bahawa untuk k ≥ 5, wujud c_k > 0 sedemikian rupa sehingga 
.
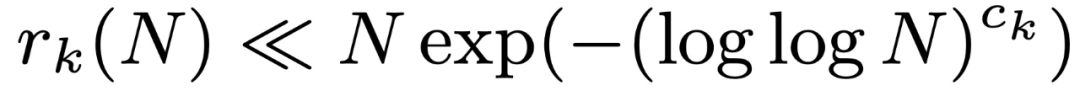Pasukan Penyelidik
Pengarang pertama karya James Leng ialah pelajar siswazah dalam matematik di University of California, Los Angeles (UCLA), dan menerima ijazah sarjana muda dari University of California, Berkeley. Dia belajar di bawah ahli matematik terkenal Terence Tao.
James Lengs Forschungsinteressen umfassen arithmetische Kombinatorik, dynamische Systeme, Fourier-Analyse usw. Seine Forschung wurde auch durch ein NSF-Graduiertenstipendium unterstützt.
. Im Sommer 2016 gewann der 16-jährige Sah die Goldmedaille bei der Internationalen Mathematikolympiade (IMO). Im folgenden Jahr ging er zum Studium am MIT.
Ashwin Sah
Während seines Studiums am MIT gab es zwei Personen, die eine wichtige Rolle in Sahs mathematischer Entwicklung spielten. Der erste ist Professor Yufei Zhao, ein Meister der diskreten Mathematik, der auch Sahs Graduiertenlehrer ist. Der Zweite ist Mehtaab Sawhney, sie haben sich im Unterricht kennengelernt und sind Freunde geworden. Später forschten die beiden gemeinsam und diskutierten verschiedene Themen im Bereich der diskreten Mathematik, wie etwa Graphentheorie, Wahrscheinlichkeitstheorie und die Eigenschaften von Zufallsmatrizen. Ashwin Sah und Mehtaab Sawhney lernten sich Ende 2017 kennen, als sie noch Studenten am MIT waren. Seitdem haben die beiden zusammen unglaubliche 57 mathematische Beweise geschrieben, von denen viele weitreichende Auswirkungen auf verschiedene Bereiche hatten.
Mehtaab Sawhney
Mehtaab Sawhney ist derzeit Assistenzprofessor an der Columbia University. Zu seinen Forschungsinteressen zählen unter anderem Kombinatorik, Wahrscheinlichkeitstheorie und theoretische Informatik.
Referenzlink: https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/
Das obige ist der detaillierte Inhalt vonZum ersten Mal seit Jahrzehnten wurden Fortschritte erzielt, die Lehrlinge Tao Zhexuan und Zhao Yufei lösten kombinatorische Mathematikprobleme. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
