
Als ich Python lernte, gab uns unser Lehrer eine Hausaufgabe: Berechnen Sie die N-te Zahl der Fibonacci-Folge.
Ich denke, es ist sehr einfach, also schreibe ich diesen Code:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n - 1) + fib(n - 2)
Später weiß ich, dass eine solche Lösung zu viel Zeit kostet.
Ich ändere die Lösung in Iteration.
def fib(n):
ls = [1,1]
for i in range(2,n):
ls.append(ls[i-1]+ls[i-2])
return ls[n-1]
Ich verwende Matplotlib Draw, die Zeit, die es kostet:
import time
import matplotlib.pyplot as plt
def bench_mark(func, *args):
# calculate the time
start = time.perf_counter()
result = func(*args)
end = time.perf_counter()
return end - start, result # return the time and the result
def fib(n):
ls = [1,1]
for i in range(2,n):
ls.append(ls[i-1]+ls[i-2])
return ls[n-1]
mark_list = []
for i in range(1,10000):
mark = bench_mark(fib,i)
mark_list.append(mark[0])
print(f"size : {i} , time : {mark[0]}")
plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()
Ergebnis hier:
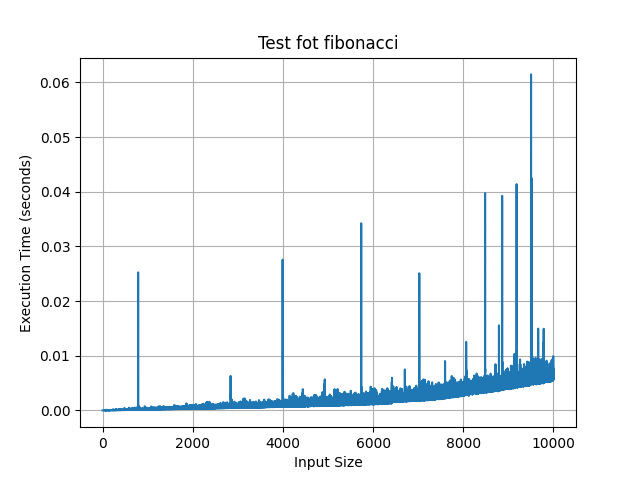
Der Zeitaufwand ist sehr kurz.
Aber ich schreibe fib(300000), kostet 5,719049899998936 Sekunden. Es ist zu lang.
Wenn ich groß bin, lerne ich CACHE, also ändere ich die Lösung, um dict zum Speichern des Ergebnisses zu verwenden.
from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
if n < 2:
return 1
else:
return fib(n - 1) + fib(n - 2)
Oder wir können den CACHE selbst schreiben.
def fib(n, cache={}):
if n in cache:
return cache[n]
elif n < 2:
return 1
else:
ls = [1, 1]
for i in range(2, n):
next_value = ls[-1] + ls[-2]
ls.append(next_value)
cache[i] = next_value
cache[n-1] = ls[-1]
return ls[-1]
Das obige ist der detaillierte Inhalt vonWie weit können Sie ein Programm zur Berechnung der Fibonacci-Folge optimieren?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Verwendung des Quellbefehls unter Linux
Verwendung des Quellbefehls unter Linux
 Kompatibilitätsprüfer
Kompatibilitätsprüfer
 So ändern Sie devc++ auf Chinesisch
So ändern Sie devc++ auf Chinesisch
 Linux-Ansichtsprozess
Linux-Ansichtsprozess
 So lösen Sie das Problem, dass die IE-Verknüpfung nicht gelöscht werden kann
So lösen Sie das Problem, dass die IE-Verknüpfung nicht gelöscht werden kann
 Was tun, wenn Chrome keine Plugins laden kann?
Was tun, wenn Chrome keine Plugins laden kann?
 c/s-Architektur und b/s-Architektur
c/s-Architektur und b/s-Architektur
 Welche Server gibt es im Web?
Welche Server gibt es im Web?




