
Um die Informationen in einer bestimmten Reihenfolge zu sortieren, oft innerhalb eines Array-ähnlichen Rahmens, müssen Sie sie anordnen. Sie können unterschiedliche Reihenfolgeanforderungen verwenden; Beliebte Methoden sind das Sortieren von Zahlen vom kleinsten zum größten oder umgekehrt oder das lexikografische Sortieren von Zeichenfolgen. Wir werden verschiedene Algorithmen behandeln, von ineffektiven, aber intuitiven Alternativen bis hin zu effizienten Algorithmen, die effektiv in Java und anderen Sprachen implementiert sind, wenn Sie daran interessiert sind, wie das Sortieren funktionieren soll.
Es gibt verschiedene Sortieralgorithmen und nicht alle sind gleich effektiv. Um sie zu vergleichen und herauszufinden, welche die beste Leistung erbringen, werden wir ihre zeitliche Komplexität analysieren.
WERBUNG Beliebter Kurs in dieser Kategorie JAVA MASTERY - Spezialisierung | 78 Kursreihe | 15 ProbetestsDas Konzept hinter Insertion Sort unterteilt den Bereich in sortierte und unsortierte Unterarrays. Der klassifizierte Teil befindet sich am Anfang der Dauer 1 und entspricht der ersten (linken) Komponente im Array. Wir bewegen uns durch das Array und erweitern den klassifizierten Teil des Arrays bei jeder Iteration um eine Komponente. Wenn wir erweitern, positionieren wir das neue Element im sortierten Unterarray. Wir tun dies, indem wir alle Elemente nach rechts verschieben, bis wir feststellen, dass wir die erste Komponente nicht ändern müssen. Wenn der fett gedruckte Teil in aufsteigender Reihenfolge sortiert wird, beispielsweise im folgenden Array, erscheint Folgendes:
Code:
public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}Ausgabe:
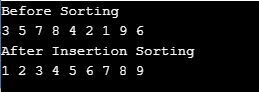
Nach dieser Methode erweiterte eine Komponente den sortierten Teil; wir haben jetzt fünf statt vier Elemente. Dies geschieht bei jeder Iteration und das gesamte Array wird am Ende sortiert.
Hinweis: Dies liegt daran, dass wir in jeder Iteration die gesamte klassifizierte Liste einzeln übertragen müssen, also O(n). Wir müssen dies für jede Komponente in jeder Tabelle tun, was bedeutet, dass sie O(n^2)-begrenzt ist.2.Wenn die Blase nicht in der erforderlichen Reihenfolge ist, ersetzt sie benachbarte Komponenten. Dies wird wiederholt, bis alle Komponenten vom Anfang des Arrays an in Ordnung sind. Wir wissen, dass, wenn es uns gelingt, die gesamte Iteration ohne Swaps durchzuführen, alle Elemente im Vergleich zu ihren angrenzenden Elementen in der gewünschten Reihenfolge waren und damit auch das gesamte Array. Der Grund für den Bubble-Sort-Algorithmus liegt darin, dass die Zahlen wie „Blasen“ in den „Boden“ gelangen. Wenn Sie nach einem bestimmten Betrag die Instanz erneut durchgehen (4 ist eine gute Instanz), werden Sie feststellen, dass sich die Zahl langsam nach rechts bewegt.
Die Schritte zur Blasensortierung sind wie folgt:
Code:
public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
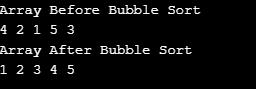
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}Ausgabe:
Auswahlsortierung teilt das Array in ein Array von Klassifizierungen auf, die nicht sortiert sind. Dieses Mal wird das Sortier-Subarray jedoch gebildet, indem am Ende des sortierten Arrays das minimale Element des unsortierten Subarrays durch Vertauschen eingefügt wird:
Code:
public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
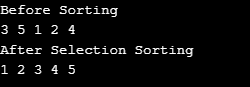
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}Ausgabe:
Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.
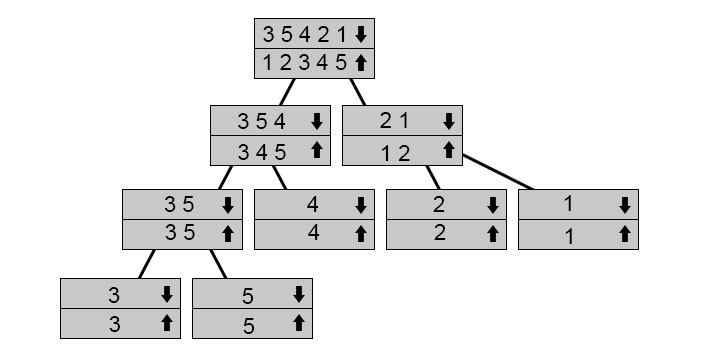
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.
Code:
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
}In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.
Output:
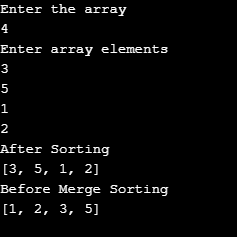
You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.
In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:
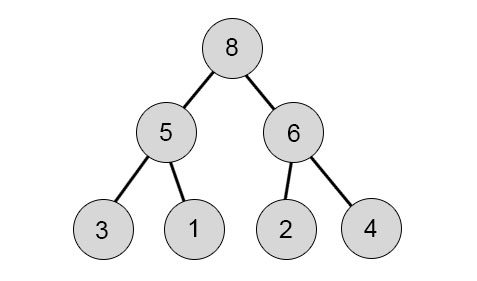
After Repeating this process again, we will get the following results:
Code:
public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}Output:
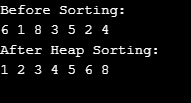
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.
Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.
Das obige ist der detaillierte Inhalt vonSortieralgorithmen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




