Mathematische Funktionen in Java

Java ist eine der nützlichsten Programmiersprachen. Es verfügt über eine Vielzahl von Anwendungen wie Architekturerstellung, Lösung von Berechnungen in der Naturwissenschaft, Erstellung von Karten usw. Um diese Aufgaben zu vereinfachen, stellt Java eine java.lang.Math-Klasse oder Mathe-Funktionen in Java bereit, die verschiedene Operationen wie Quadrat- und Exponentialoperationen ausführt , Decke, Logarithmus, Kubik, Bauchmuskeln, Trigonometrie, Quadratwurzel, Boden usw.

WERBUNG Beliebter Kurs in dieser Kategorie JAVA MASTERY - Spezialisierung | 78 Kursreihe | 15 Probetests

Starten Sie Ihren kostenlosen Softwareentwicklungskurs

Webentwicklung, Programmiersprachen, Softwaretests und andere

Dieser Kurs bietet zwei Felder, die die Grundlagen des Mathematikunterrichts bilden. Sie sind,

• „e“, die Basis des natürlichen Logarithmus (718281828459045)
• „pi“, das ist das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser (141592653589793)

Verschiedene Mathefunktionen in Java

Java bietet eine Fülle mathematischer Methoden. Sie können wie folgt klassifiziert werden:

• Grundlegende mathematische Methoden
• Trigonometrische mathematische Methoden
• Logarithmische mathematische Methoden
• Hyperbolische mathematische Methoden
• Winkelmathematische Methoden

Lassen Sie uns nun einen genaueren Blick darauf werfen.

1. Grundlegende mathematische Methoden

Zum besseren Verständnis können wir die oben genannten Methoden wie unten gezeigt in einem Java-Programm implementieren:

dargestellt

Methode	Rückgabewert	Argumente	Beispiel
abs()	Absoluter Wert des Arguments. d.h. positiver Wert	long, int, float, double	int n1 = Math.abs (80)  //n1=80 int n2 =Math.abs (-60) //n2=60
sqrt()	Die Quadratwurzel des Arguments	doppelt	double n= Math.sqrt (36.0) // n=6.0
cbt()	Kubikwurzel des Arguments	doppelt	double n= Math.cbrt (8.0) // n=2.0
max()	Maximum der beiden im Argument übergebenen Werte	long, int, float, double	int n=Math.max(15,80) //n=80
min()	Minimum der beiden im Argument übergebenen Werte	long, int, float, double	int n=Math.min(15,80) //n=15
ceil()	Rundet den Gleitkommawert auf einen ganzzahligen Wert auf	doppelt	double n=Math.ceil(6.34) //n=7.0
floor()	Rundet den Gleitkommawert auf einen ganzzahligen Wert ab	doppelt	double n=Math.floor(6.34) //n=6.0
round()	Rundet den Float- oder Double-Wert entweder auf oder ab auf einen ganzzahligen Wert	doppelt, schwebend	double n = Math.round(22.445);//n=22.0 double n2 = Math.round(22.545); //n=23,0
pow()	Wert des ersten Parameters erhöht auf den zweiten Parameter	doppelt	double n= Math.pow(2.0, 3.0) //n=8.0
zufällig()	Eine Zufallszahl zwischen 0 und 1	doppelt	double n= Math.random() //n= 0,2594036953954201
signum()	Vorzeichen des übergebenen Parameters. Wenn positiv, wird 1 angezeigt. Wenn negativ, wird -1 angezeigt. Wenn 0, wird 0 angezeigt	doppelt, schwebend	double n = Mathe. signum (22.4);//n=1.0 double n2 = Math. signum (-22,5);//n=-1,0
addExact()	Summe der Parameter. Eine Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis einen Long- oder Int-Wert überschreitet.	int, long	int n= Math.addExact(35, 21)//n=56
incrementExact()	Parameter um 1 erhöht. Die Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis den int-Wert überläuft.	int, long	int n=Mathe. incrementExact(36) //n=37
subtractExact()	Unterschied der Parameter. Die Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis den int-Wert überschreitet.	int, long	int n= Math.subtractExact(36, 11) //n=25
multiplyExact()	Summe der Parameter. Eine Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis einen Long- oder Int-Wert überschreitet.	int, long	int n= Math.multiplyExact(5, 5) //n=25
decrementExact()	Parameter um 1 dekrementiert. Die Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis einen Int- oder Long-Wert überläuft.	int, long	int n=Mathe. decrementExact (36) //n=35
negateExact()	Die Negation des Parameters. Die Ausnahme wird ausgelöst, wenn das erhaltene Ergebnis einen Int- oder Long-Wert überschreitet.	int, long	int n=Mathe. negateExact(36) //n=-36
copySign()	Absoluter Wert des ersten Parameters zusammen mit dem im zweiten Parameter angegebenen Vorzeichen	double,float	double d= Math.copySign(29.3,-17.0) //n=-29.3
floorDiv()	Dividieren Sie den ersten Parameter durch den zweiten Parameter und die Bodenoperation wird ausgeführt.	long, int	int n= Math.floorDiv(25, 3) //n=8
hypot()	Berechnen Sie die Summe der Quadrate der Parameter und führen Sie eine Quadratwurzeloperation durch. Ein zwischenzeitlicher Überlauf oder Unterlauf sollte nicht vorhanden sein.	doppelt	double n=Math.hypot(4,3) //n=5.0
getExponent()	unvoreingenommener Exponent. Dieser Exponent wird in Double oder Float	int	double n=Math.getExponent(50.45) //n=5

Code:

//Java program to implement basic math functions
public class JavaMathFunctions {
public static void main(String[] args) {
int n1 = Math.abs(80);
System.out.println("absolute value of 80 is: "+n1);
int n2 = Math.abs(-60);
System.out.println("absolute value of -60 is: "+n2);
double n3 = Math.sqrt(36.0);
System.out.println("Square root of 36.0 is: "+n3);
double n4 = Math.cbrt(8.0);
System.out.println("cube root 0f 8.0 is: "+n4);
int n5= Math.max(15,80);
System.out.println("max value is: "+n5);
int n6 =Math.min(15,80);
System.out.println("min value is: "+n6);
double n7 = Math.ceil(6.34);
System.out.println("ceil value of 6.34 is "+n7);
double n8 = Math.floor(6.34);
System.out.println("floor value of 6.34 is: "+n8);
double n9 = Math.round(22.445);
System.out.println("round value of 22.445 is: "+n9);
double n10 = Math.round(22.545);
System.out.println("round value of 22.545 is: "+n10);
double n11= Math.pow(2.0, 3.0);
System.out.println("power value is: "+n11);
double n12= Math.random();
System.out.println("random value is: "+n12);
double n13 = Math. signum (22.4);
System.out.println("signum value of 22.4 is: "+n13);
double n14 = Math. signum (-22.5);
System.out.println("signum value of 22.5 is: "+n14);
int n15= Math.addExact(35, 21);
System.out.println("added value is: "+n15);
int n16=Math. incrementExact(36);
System.out.println("increment of 36 is: "+n16);
int n17 = Math.subtractExact(36, 11);
System.out.println("difference is: "+n17);
int n18 = Math.multiplyExact(5, 5);
System.out.println("product is: "+n18);
int n19 =Math. decrementExact (36);
System.out.println("decrement of 36 is: "+n19);
int n20 =Math. negateExact(36);
System.out.println("negation value of 36 is: "+n20);
}
}

Output:

2. Trigonometric Math Methods

Following is the Java program to implement trigonometric math functions mentioned in the table:

Method	Return value	Arguments	Example
sin()	Sine value of the parameter	double	double num1 = 60; //Conversion of value to radians double value = Math.toRadians(num1); print Math.sine (value) //output is 0.8660254037844386
cos()	Cosine value of the parameter	double	double num1 = 60; //Conversion of value to radians double value = Math.toRadians(num1); print Math.cos (value) //output is           0.5000000000000001
tan()	tangent value of the parameter	double	double num1 = 60; //Conversion of value to radians double value = Math.toRadians(num1); print Math.tan(value) //output is 1.7320508075688767
asin()	Arc Sine value of the parameter. Or Inverse sine value of the parameter	double	Math.asin(1.0) // 1.5707963267948966
acos()	Arc cosine value of the parameter Or Inverse Cosine value of the parameter	double	Math.acos(1.0) //0.0
atan()	Arctangent value of the parameter Or Inverse tangent value of the parameter	double	Math.atan(6.267) // 1.4125642791467878

Code:

//Java program to implement trigonometric math functions
public class JavaMathFunctions {
public static void main(String[] args) {
double num1 = 60;
// Conversion of value to radians
double value = Math.toRadians(num1);
System.out.println("sine value is : "+Math.sin(value));
System.out.println("cosine value is : "+Math.cos(value));
System.out.println("tangent value is : "+Math.tan(value));
double num2 = 1.0;
System.out.println("acosine value is : "+Math.acos(num2));
System.out.println("asine value is : "+Math.asin(num2));
double num3 = 6.267;
System.out.println("atangent value is : "+Math.atan(num3)); <strong>Output:</strong>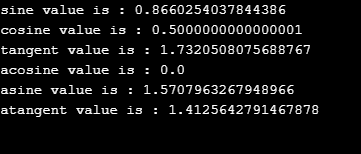

3. Logarithmic Math Methods

Following is the sample program that implements Logarithmic math methods:

Method	Return Value	Arguments	Example
expm1()	Calculate E’s power and minus 1 from it. E is Euler’s number. So here, it is ex-1.	double	double n = Math.expm1(2.0) // n = 6.38905609893065
exp()	E’s power to the given parameter. That is, ex	double	double n=Math.exp(2.0) //n = 7.38905609893065
log()	Natural logarithm of parameter	double	double n=Math.log(38.9) //n=3.6609942506244004
log10()	Base 10 logarithm of parameter	double	double n =  Math.log10(38.9) //n= 1.5899496013257077
log1p()	Natural logarithm of the sum of parameter and one. ln(x+1)	double	double n =   Math.log1p(26) //n= 3.295836866004329

Code:

//Java program to implement logarithmic math functions
public class JavaMathFunctions {
public static void main(String[] args) {
double n1 = Math.expm1(2.0);
double n2 = Math.exp(2.0);
double n3 = Math.log(38.9);
double n4 = Math.log10(38.9);
double n5 = Math.log1p(26);
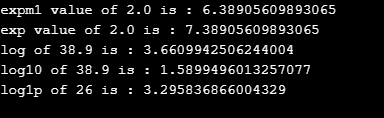
System.out.println("expm1 value of 2.0 is : "+n1);
System.out.println("exp value of 2.0 is : "+n2);
System.out.println("log of 38.9 is : "+n3);
System.out.println("log10 of 38.9 is : "+n4);
System.out.println("log1p of 26 is : "+n5);
}}

Output:

4. Hyperbolic Math Methods

Following is the Java program to implement hyperbolic math functions mentioned in the table:

Method	Return value	Arguments	Example
sinh()	Hyperbolic Sine value of the parameter. i.e (ex – e -x)/2 Here, E is the Euler’s number.	double	double num1=Math.sinh (30) //output is 5.343237290762231E12
cosh()	Hyperbolic Cosine value of the parameter. i.e. (ex + e -x)/2 Here, E is the Euler’s number.	double	double num1 = Math.cosh (60.0) //output is 5.710036949078421E25
tanh()	Hyperbolic tangent value of the parameter	double	double num1= Math.tanh (60.0) //output is 1.0

Code:

//Java program to implement HYPERBOLIC math functions
public class JavaMathFunctions {
public static void main(String[] args) {
double n1 = Math.sinh (30);
double n2 = Math.cosh (60.0);
double n3 = Math.tanh (60.0);
System.out.println("Hyperbolic sine value of 300 is : "+n1);
System.out.println("Hyperbolic cosine value of 60.0 is : "+n2);
System.out.println("Hyperbolic tangent value of 60.0 is : "+n3);
}
}

Output:

5. Angular Math Methods

Method	Return Value	Arguments	Example
toRadians()	Degree angle converts to radian angle	double	double n = Math.toRadians(180.0) //n= 3.141592653589793
toDegrees()	Radian angle converts to Degree angle	double	double n = Math. toDegrees (Math.PI) //n=180.0

 Now, let us see a sample program to demonstrate Angular Math methods.

Code:

//Java program to implement Angular math functions
public class JavaMathFunctions {
public static void main(String[] args) {
double n1 = Math.toRadians(180.0);
double n2 = Math. toDegrees (Math.PI);
System.out.println("Radian value of 180.0 is : "+n1);
System.out.println("Degree value of pi is : "+n2);
}
}

Output:

Conclusion

Java offers a wide variety of math functions to perform different tasks such as scientific calculations, architecture designing, structure designing, building maps, etc. This document discusses several basic, trigonometric, logarithmic and angular math functions in detail with sample programs and examples.

Das obige ist der detaillierte Inhalt vonMathematische Funktionen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!