
Ein binärer Suchbaum ist eine Datenstruktur, die es uns ermöglicht, in kurzer Zeit eine sortierte Liste von Zahlen zu führen. Er wird auch Binärbaum genannt, da jeder Baumknoten nur zwei Geschwister haben kann. Der binäre Suchbaum kann verwendet werden, um nach dem Vorhandensein einer Zahl zu suchen. es wird als Suchbaum bezeichnet. Die Laufzeitkomplexität beträgt O(log(n)) Zeit; Die Merkmale, die einen binären Suchbaum von einem einfachen Binärbaum unterscheiden, sind wie folgt –
Starten Sie Ihren kostenlosen Softwareentwicklungskurs
Webentwicklung, Programmiersprachen, Softwaretests und andere
1. Die Knoten des linken Teilbaums sind alle kleiner als der Wurzelknoten.
2. Die Knoten des rechten Teilbaums sind alle größer als der Wurzelknoten.
3. Jeder Knoten der Teilbäume besteht ebenfalls aus BSTs, was bedeutet, dass sie die gleichen zwei Eigenschaften wie der Knoten selbst haben.
1. Das angegebene Array sei:
Gegebenes Array: [8, 6, 2, 7, 9, 12, 4, 10]
2. Beginnen wir mit dem obersten Element 43. Fügen Sie 43 als Wurzel des Baums ein.
3. Wenn das nächste Element kleiner als das Wurzelknotenelement ist, sollte es als Wurzel des linken Unterbaums eingefügt werden.
4. Wenn nicht, sollte es als Wurzel des rechten Unterbaums eingefügt werden.
Das Bild unten zeigt den Prozess der Erstellung eines binären Suchbaums unter Verwendung der bereitgestellten Elemente.
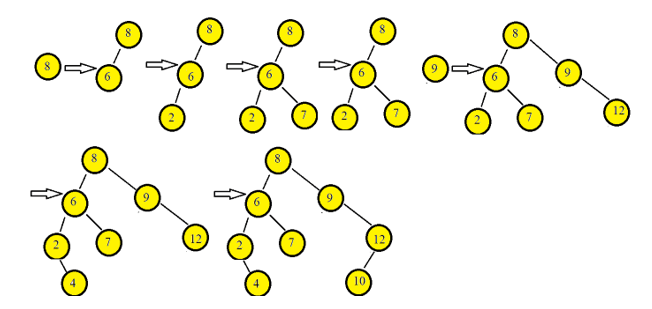
Binäre Suchbaumoperationen:
Die vom binären Suchbaum in Java unterstützten Operationen werden in der folgenden Liste angezeigt –
1. Suchen in BST – In einem binären Suchbaum die Position eines bestimmten Elements finden.
2. Einfügen in BST – Durch das Hinzufügen eines neuen Elements zum binären Suchbaum an der richtigen Stelle wird sichergestellt, dass die Eigenschaft des binären Suchbaums nicht beschädigt wird.
3. Löschen in BST – Entfernen Sie einen bestimmten Knoten in einem binären Suchbaum. Abhängig von der Anzahl der untergeordneten Knoten eines Knotens kann es jedoch verschiedene Löschszenarien geben.
Beispiel für einen binären Suchbaum in Java zum Ausführen einer Operation am binären Suchbaum –
// Das Programm kann in Eclipse IDE, JAVA 11 getestet werden
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}Ausgabe:
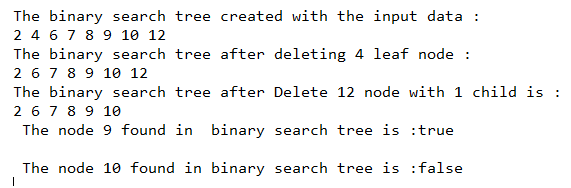
Wie im obigen Programm wird die Klasse „binarySearchTree“ erstellt, die einen weiteren inneren Klassenknoten sowie den Konstruktor und die Methoden enthält. Die in der Klasse definierten Methoden sind deleteKey(), delete(), minKey(), insertKey(), insert(), inorder(), searchKey() und search(), um die spezifischen Operationen auszuführen. In der Hauptfunktion wird das Klassenobjekt „binarySearchTree“ erstellt, einige Elemente darin eingefügt und als nächstes die Methoden der binären Search Tree-Klasse für ihr Objekt aufgerufen, wie in der obigen Ausgabe zu sehen.
Der binäre Suchbaum wird auch als Binärbaum bezeichnet, da jeder Baumknoten nur zwei Geschwister haben kann. Ein binärer Suchbaum ist eine Datenstruktur, die es ermöglicht, in kurzer Zeit eine sortierte Liste von Zahlen zu führen. Die Operation, die im binären Suchbaum ausgeführt werden kann: Durchlaufen, Einfügen, Löschen und Suchen.
Das obige ist der detaillierte Inhalt vonBinärer Suchbaum in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




