Kürzeste Wege finden

Der kürzeste Pfad zwischen zwei Eckpunkten ist ein Pfad mit den minimalen Gesamtgewichten.
Bei einem Diagramm mit nichtnegativen Gewichten an den Kanten wurde von Edsger Dijkstra, einem niederländischen Informatiker, ein bekannter Algorithmus zum Finden eines kürzesten Pfades zwischen zwei Eckpunkten entdeckt. Um einen kürzesten Weg vom Scheitelpunkt s zum Scheitelpunkt v zu finden, findet Dijkstras Algorithmus den kürzesten Weg von s zu allen Scheitelpunkten. Daher ist Dijkstras Algorithmus als Single-Source-Algorithmus für den kürzesten Weg bekannt. Der Algorithmus verwendet cost[v], um die Kosten eines kürzesten Pfades vom Scheitelpunkt v zum Quellscheitelpunkt s zu speichern. Kosten[s] beträgt 0. Weisen Sie cost[v] zunächst unendlich für alle anderen Scheitelpunkte zu. Der Algorithmus findet wiederholt einen Scheitelpunkt u in V – T mit den kleinsten Kosten[u] und verschiebt u nach T .

Der Algorithmus wird im folgenden Code beschrieben.

Input: a graph G = (V, E) with non-negative weights
Output: a shortest path tree with the source vertex s as the root
 1 ShortestPathTree getShortestPath(s) {
 2 Let T be a set that contains the vertices whose
 3 paths to s are known; Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T < n) {
 7 Find u not in T with the smallest cost[u];
 8 Add u to T;
 9 for (each v not in T and (u, v) in E)
10 if (cost[v] > cost[u] + w(u, v)) {
11 cost[v] = cost[u] + w(u, v); parent[v] = u;
12 }
13 }
14 }

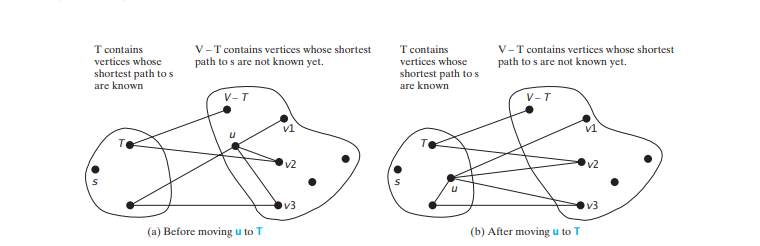
Dieser Algorithmus ist dem von Prim zum Finden eines minimalen Spannbaums sehr ähnlich. Beide Algorithmen unterteilen die Eckpunkte in zwei Mengen: T und V - T. Im Fall des Prim-Algorithmus enthält die Menge T die Eckpunkte, die bereits zum Baum hinzugefügt wurden. Im Fall von Dijkstra enthält die Menge T die Eckpunkte, deren kürzeste Wege zur Quelle gefunden wurden. Beide Algorithmen finden wiederholt einen Knoten aus V – T und fügen ihn zu T hinzu. Im Fall des Prim-Algorithmus grenzt der Scheitelpunkt an einen Scheitelpunkt in der Menge mit dem minimalen Gewicht auf der Kante. Im Dijkstra-Algorithmus grenzt der Scheitelpunkt an einen Scheitelpunkt in der Menge mit den minimalen Gesamtkosten für die Quelle.

Der Algorithmus setzt zunächst cost[s] auf 0 (Zeile 4) und setzt cost[v] für alle anderen Eckpunkte auf unendlich. Anschließend wird kontinuierlich ein Scheitelpunkt (z. B. u) von V – T in T mit den kleinsten Kosten[u] hinzugefügt (Zeilen 7– 8), wie in Abbildung unten dargestellt a. Nach dem Hinzufügen von u zu T aktualisiert der Algorithmus cost[v] und parent[v] für jedes v nicht in T, wenn (u, v) in T ist und Kosten[v] > cost[u] + w(u, v) (Zeilen 10–11).

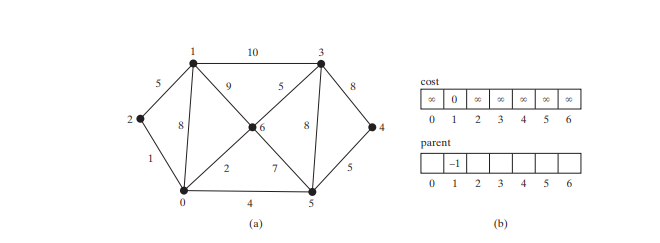
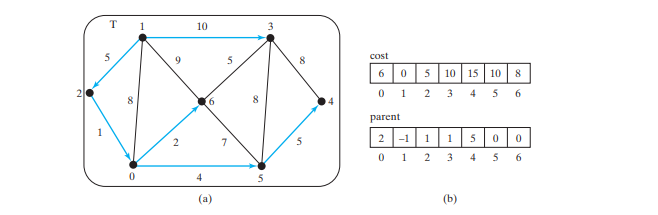
Lassen Sie uns den Dijkstra-Algorithmus anhand der Grafik in Abbildung unten veranschaulichen. Angenommen, der Quellscheitelpunkt ist 1. Daher ist Kosten[1] = 0 und die Kosten für alle anderen Eckpunkte betragen zunächst ∞, wie in Abbildung unten b dargestellt. Wir verwenden parent[i], um das übergeordnete Element von i im Pfad zu bezeichnen. Der Einfachheit halber setzen Sie den übergeordneten Knoten des Quellknotens auf -1.

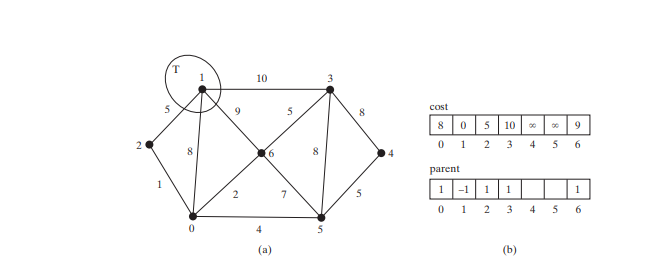
Anfangs eingestellt ist T leer. Der Algorithmus wählt den Scheitelpunkt mit den geringsten Kosten aus. In diesem Fall ist der Scheitelpunkt 1. Der Algorithmus addiert 1 zu T, wie in Abbildung unten a dargestellt. Anschließend werden die Kosten für jeden an 1 angrenzenden Scheitelpunkt angepasst. Die Kosten für die Scheitelpunkte 2, 0, 6 und 3 und ihre Eltern werden nun aktualisiert, wie in Abbildung unten b gezeigt.

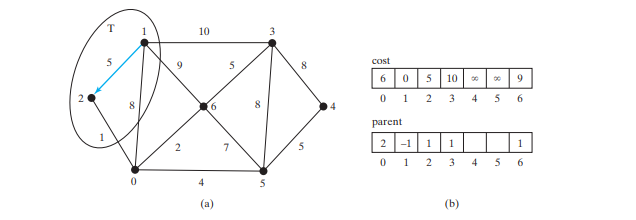
Scheitelpunkte 2, 0, 6 und 3 liegen neben dem Quellscheitelpunkt und dem Scheitelpunkt 2 ist derjenige in V-T mit den geringsten Kosten, also addieren Sie 2 zu T, wie in der Abbildung unten gezeigt, und aktualisieren Sie die Kosten und das übergeordnete Element für Scheitelpunkte in V-T und angrenzend an 2. Kosten[0] wird jetzt auf 6 aktualisiert und sein übergeordnetes Element wird auf 2 gesetzt. Die Pfeillinie von 1 bis 2 zeigt an, dass 1 das übergeordnete Element von 2 ist, nachdem 2 hinzugefügt wurde T.

Jetzt enthält T {1, 2}. Scheitelpunkt 0 ist derjenige in V-T mit den geringsten Kosten, also fügen Sie 0 zu T hinzu, wie in der Abbildung unten gezeigt, und aktualisieren Sie den Kosten und übergeordnetes Element für Scheitelpunkte in V-T und angrenzend an 0, falls zutreffend. Kosten[5] wird jetzt auf 10 aktualisiert und sein übergeordnetes Element wird auf 0 gesetzt und Kosten[6] wird jetzt auf 8 und sein übergeordnetes Element ist auf 0 gesetzt.

Jetzt enthält

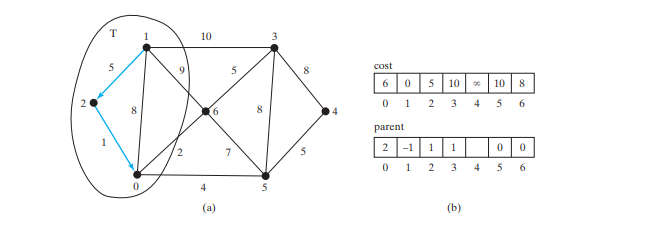
T {1, 2, 0}. Scheitelpunkt 6 ist derjenige in V-T mit den geringsten Kosten, also fügen Sie 6 zu T hinzu, wie in der Abbildung unten gezeigt, und aktualisieren Sie den Kosten und übergeordnetes Element für Eckpunkte in V-T und angrenzend an 6, falls zutreffend.

Jetzt enthält

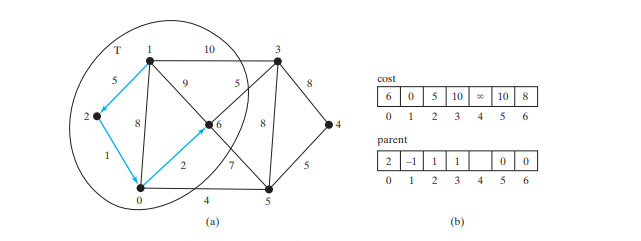
T {1, 2, 0, 6}. Scheitelpunkt 3 oder 5 ist derjenige in V-T mit den geringsten Kosten. Sie können entweder 3 oder 5 zu T hinzufügen. Fügen wir 3 zu T hinzu, wie in der Abbildung unten gezeigt, und aktualisieren wir die Kosten und das übergeordnete Element für Scheitelpunkte in V-T und neben 3 gegebenenfalls. Kosten[4] wird jetzt auf 18 aktualisiert und sein übergeordnetes Element ist auf 3 eingestellt.

Jetzt enthält

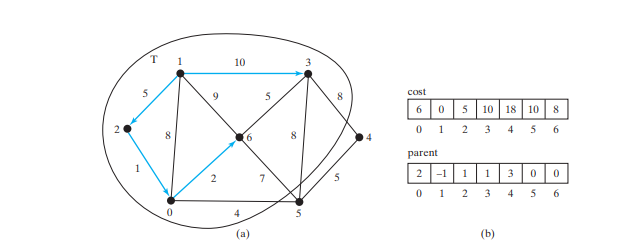
T {1, 2, 0, 6, 3}. Scheitelpunkt 5 ist derjenige in V-T mit den geringsten Kosten, also fügen Sie 5 zu T hinzu, wie in der Abbildung unten gezeigt, und aktualisieren Sie den Kosten und übergeordnetes Element für Scheitelpunkte in V-T und angrenzend an 5, falls zutreffend. Kosten[4] wird jetzt auf 10 aktualisiert und sein übergeordnetes Element ist auf 5 eingestellt.

Jetzt enthält

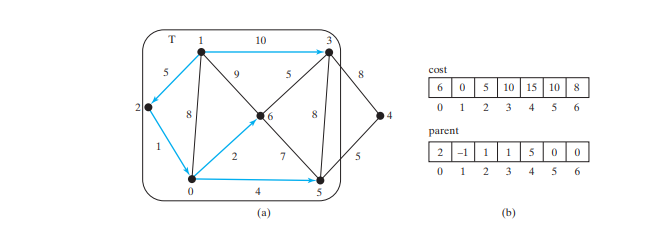
T {1, 2, 0, 6, 3, 5}. Scheitelpunkt 4 ist derjenige in V-T mit den geringsten Kosten, also addieren Sie 4 zu T, wie in der Abbildung unten gezeigt.

Wie Sie sehen können, findet der Algorithmus im Wesentlichen alle kürzesten Pfade von einem Quellscheitelpunkt aus, wodurch ein Baum entsteht, der am Quellscheitelpunkt wurzelt. Wir nennen diesen Baum einen

Single-Source-All-Shortest-Path-Baum (oder einfach einen Shortest-Path-Baum). Um diesen Baum zu modellieren, definieren Sie eine Klasse mit dem Namen ShortestPathTree, die die Klasse Tree erweitert, wie in der Abbildung unten dargestellt. ShortestPathTree ist als innere Klasse in WeightedGraph in den Zeilen 200–224 in WeightedGraph.java definiert.

Die Methode

getShortestPath(int sourceVertex) wurde in den Zeilen 156–197 in WeightedGraph.java implementiert. Die Methode setzt cost[sourceVertex] auf 0 (Zeile 162) und cost[v] auf unendlich für alle anderen Scheitelpunkte (Zeilen 159–161). Das übergeordnete Element von sourceVertex wird auf -1 gesetzt (Zeile 166). T ist eine Liste, die die Scheitelpunkte speichert, die dem Baum mit dem kürzesten Pfad hinzugefügt wurden (Zeile 169). Wir verwenden eine Liste für T anstelle einer Menge, um die Reihenfolge der zu T hinzugefügten Eckpunkte aufzuzeichnen.

Anfangs ist

T leer. Um T zu erweitern, führt die Methode die folgenden Operationen aus:

1. Find the vertex u with the smallest cost[u] (lines 175–181) and add it into T (line 183).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > cost[u] + w(u, v) (lines 186–192).

Once all vertices from s are added to T, an instance of ShortestPathTree is created (line 196).

The ShortestPathTree class extends the Tree class (line 200). To create an instance of ShortestPathTree, pass sourceVertex, parent, T, and cost (lines 204–205). sourceVertex becomes the root in the tree. The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n^3).

Dijkstra’s algorithm is a combination of a greedy algorithm and dynamic programming. It is a greedy algorithm in the sense that it always adds a new vertex that has the shortest distance to the source. It stores the shortest distance of each known vertex to the source and uses it later to avoid redundant computing, so Dijkstra’s algorithm also uses dynamic programming.

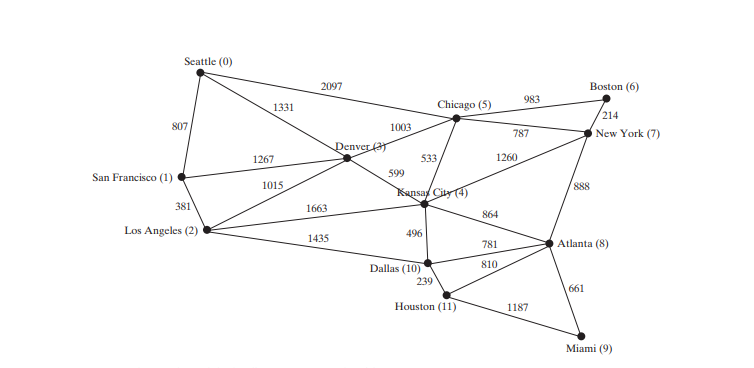
The code below gives a test program that displays the shortest paths from Chicago to all other cities in Figure below and the shortest paths from vertex 3 to all vertices for the graph in Figure below a, respectively.

package demo;

public class TestShortestPath {

    public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
        WeightedGraph<String>.ShortestPathTree tree1 = graph1.getShortestPath(graph1.getIndex("Chicago"));
        tree1.printAllPaths();

        // Display shortest paths from Houston to Chicago       
        System.out.println("Shortest path from Houston to Chicago: ");
        java.util.List<String> path = tree1.getPath(graph1.getIndex("Houston"));
        for(String s: path) {
            System.out.print(s + " ");
        }

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
        WeightedGraph<Integer>.ShortestPathTree tree2 = graph2.getShortestPath(3);
        System.out.println("\n");
        tree2.printAllPaths();
    }

}

All shortest paths from Chicago are:
A path from Chicago to Seattle: Chicago Seattle (cost: 2097.0)
A path from Chicago to San Francisco:
Chicago Denver San Francisco (cost: 2270.0)
A path from Chicago to Los Angeles:
Chicago Denver Los Angeles (cost: 2018.0)
A path from Chicago to Denver: Chicago Denver (cost: 1003.0)
A path from Chicago to Kansas City: Chicago Kansas City (cost: 533.0)
A path from Chicago to Chicago: Chicago (cost: 0.0)
A path from Chicago to Boston: Chicago Boston (cost: 983.0)
A path from Chicago to New York: Chicago New York (cost: 787.0)
A path from Chicago to Atlanta:
Chicago Kansas City Atlanta (cost: 1397.0)
A path from Chicago to Miami:
Chicago Kansas City Atlanta Miami (cost: 2058.0)
A path from Chicago to Dallas: Chicago Kansas City Dallas (cost: 1029.0)
A path from Chicago to Houston:
Chicago Kansas City Dallas Houston (cost: 1268.0)
Shortest path from Houston to Chicago:
Houston Dallas Kansas City Chicago

All shortest paths from 3 are:
A path from 3 to 0: 3 1 0 (cost: 5.0)
A path from 3 to 1: 3 1 (cost: 3.0)
A path from 3 to 2: 3 2 (cost: 4.0)
A path from 3 to 3: 3 (cost: 0.0)
A path from 3 to 4: 3 4 (cost: 6.0)

The program creates a weighted graph for Figure above in line 27. It then invokes the getShortestPath(graph1.getIndex("Chicago")) method to return a Path object that contains all shortest paths from Chicago. Invoking printAllPaths() on the ShortestPathTree object displays all the paths (line 30).

The graphical illustration of all shortest paths from Chicago is shown in Figure below. The shortest paths from Chicago to the cities are found in this order: Kansas City, New York, Boston, Denver, Dallas, Houston, Atlanta, Los Angeles, Miami, Seattle, and San Francisco.

Das obige ist der detaillierte Inhalt vonKürzeste Wege finden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!