Gewichtete Diagramme und Anwendungen
Ein Diagramm ist ein gewichtetes Diagramm, wenn jeder Kante ein Gewicht zugewiesen wird. Gewichtete Diagramme haben viele praktische Anwendungen.
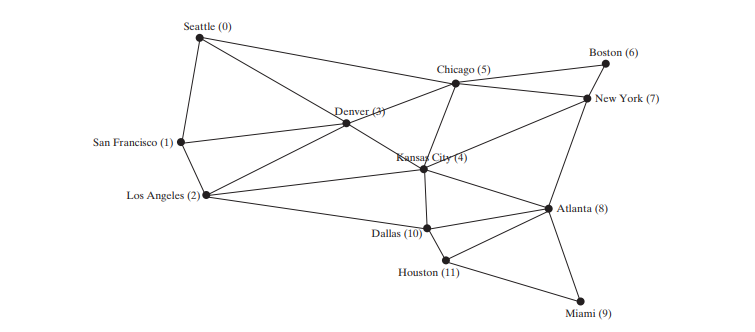
Die obige Abbildung geht davon aus, dass die Grafik die Anzahl der Flüge zwischen Städten darstellt. Mithilfe des BFS können Sie die geringste Anzahl an Flügen zwischen zwei Städten ermitteln. Gehen Sie davon aus, dass die Kanten die Fahrstrecken zwischen den Städten darstellen, wie in der Abbildung unten dargestellt. Wie ermitteln Sie die minimalen Gesamtentfernungen für die Verbindung aller Städte? Wie findet man den kürzesten Weg zwischen zwei Städten? In diesem Kapitel wird auf diese Fragen eingegangen. Ersteres ist als Minimum Spanning Tree (MST)-Problem und letzteres als Problem des kürzesten Pfades bekannt.
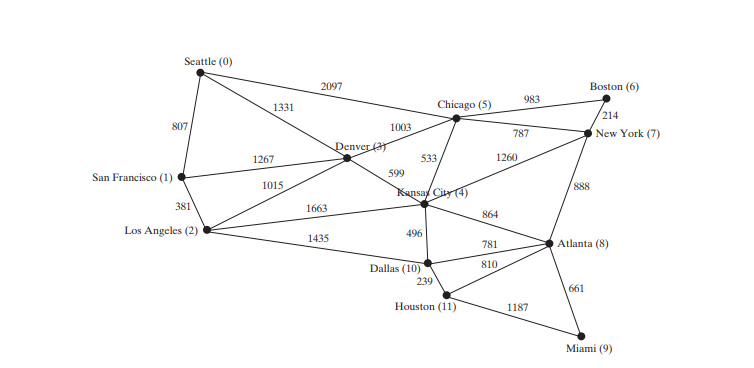
Im vorangegangenen Kapitel wurde das Konzept der Graphen vorgestellt. Sie haben gelernt, wie Sie Kanten mithilfe von Kantenarrays, Kantenlisten, Adjazenzmatrizen und Adjazenzlisten darstellen und wie Sie ein Diagramm mithilfe der Schnittstelle Graph, der Klasse AbstractGraph und der Klasse UnweightedGraph Klasse. Im vorherigen Kapitel wurden außerdem zwei wichtige Techniken zum Durchlaufen von Diagrammen vorgestellt: Tiefensuche und Breitensuche sowie angewandte Durchquerung zur Lösung praktischer Probleme. In den folgenden Beiträgen werden gewichtete Diagramme vorgestellt. Sie lernen den Algorithmus zum Finden eines minimalen Spannbaums in Post und den Algorithmus zum Finden kürzester Pfade in Post kennen.
Das obige ist der detaillierte Inhalt vonGewichtete Diagramme und Anwendungen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Wie funktioniert der Klassenladungsmechanismus von Java, einschließlich verschiedener Klassenloader und deren Delegationsmodelle?
Mar 17, 2025 pm 05:35 PM
Wie funktioniert der Klassenladungsmechanismus von Java, einschließlich verschiedener Klassenloader und deren Delegationsmodelle?
Mar 17, 2025 pm 05:35 PM
Mit der Klassenbelastung von Java wird das Laden, Verknüpfen und Initialisieren von Klassen mithilfe eines hierarchischen Systems mit Bootstrap-, Erweiterungs- und Anwendungsklassenloadern umfasst. Das übergeordnete Delegationsmodell stellt sicher
 Wie implementiere ich mehrstufige Caching in Java-Anwendungen mit Bibliotheken wie Koffein oder Guava-Cache?
Mar 17, 2025 pm 05:44 PM
Wie implementiere ich mehrstufige Caching in Java-Anwendungen mit Bibliotheken wie Koffein oder Guava-Cache?
Mar 17, 2025 pm 05:44 PM
In dem Artikel wird in der Implementierung von mehrstufigem Caching in Java mithilfe von Koffein- und Guava-Cache zur Verbesserung der Anwendungsleistung erläutert. Es deckt die Einrichtungs-, Integrations- und Leistungsvorteile sowie die Bestrafung des Konfigurations- und Räumungsrichtlinienmanagements ab
 Wie kann ich JPA (Java Persistence-API) für Objektrelationszuordnungen mit erweiterten Funktionen wie Caching und faulen Laden verwenden?
Mar 17, 2025 pm 05:43 PM
Wie kann ich JPA (Java Persistence-API) für Objektrelationszuordnungen mit erweiterten Funktionen wie Caching und faulen Laden verwenden?
Mar 17, 2025 pm 05:43 PM
In dem Artikel werden mit JPA für Objektrelationszuordnungen mit erweiterten Funktionen wie Caching und faulen Laden erläutert. Es deckt Setup, Entity -Mapping und Best Practices zur Optimierung der Leistung ab und hebt potenzielle Fallstricke hervor. [159 Charaktere]
 Wie benutze ich Maven oder Gradle für das fortschrittliche Java -Projektmanagement, die Erstellung von Automatisierung und Abhängigkeitslösung?
Mar 17, 2025 pm 05:46 PM
Wie benutze ich Maven oder Gradle für das fortschrittliche Java -Projektmanagement, die Erstellung von Automatisierung und Abhängigkeitslösung?
Mar 17, 2025 pm 05:46 PM
In dem Artikel werden Maven und Gradle für Java -Projektmanagement, Aufbau von Automatisierung und Abhängigkeitslösung erörtert, die ihre Ansätze und Optimierungsstrategien vergleichen.
 Wie erstelle und verwende ich benutzerdefinierte Java -Bibliotheken (JAR -Dateien) mit ordnungsgemäßem Versioning und Abhängigkeitsmanagement?
Mar 17, 2025 pm 05:45 PM
Wie erstelle und verwende ich benutzerdefinierte Java -Bibliotheken (JAR -Dateien) mit ordnungsgemäßem Versioning und Abhängigkeitsmanagement?
Mar 17, 2025 pm 05:45 PM
In dem Artikel werden benutzerdefinierte Java -Bibliotheken (JAR -Dateien) mit ordnungsgemäßem Versioning- und Abhängigkeitsmanagement erstellt und verwendet, wobei Tools wie Maven und Gradle verwendet werden.




