
Ich möchte Ihnen die nützlichste Methode in Python vorstellen, np.einsum.
Mit np.einsum (und seinen Gegenstücken in Tensorflow und JAX) können Sie komplizierte Matrix- und Tensoroperationen auf äußerst klare und prägnante Weise schreiben. Ich habe auch festgestellt, dass seine Klarheit und Prägnanz die mentale Überlastung, die mit der Arbeit mit Tensoren einhergeht, erheblich lindert.
Und es ist eigentlich ziemlich einfach zu erlernen und zu verwenden. So funktioniert es:
In np.einsum haben Sie ein tiefgestelltes Zeichenfolgenargument und einen oder mehrere Operanden:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
Das Subscripts-Argument ist eine „Minisprache“, die Numpy sagt, wie die Achsen der Operanden manipuliert und kombiniert werden sollen. Am Anfang ist es etwas schwierig zu lesen, aber wenn man den Dreh raus hat, ist es nicht schlimm.
Als erstes Beispiel verwenden wir np.einsum, um die Achsen einer Matrix A zu vertauschen (auch bekannt als „transponieren“):
M = np.einsum('ij->ji', A)
Die Buchstaben i und j sind an die erste und zweite Achse von A gebunden. Numpy bindet Buchstaben in der Reihenfolge, in der sie erscheinen, an Achsen, aber Numpy ist es egal, welche Buchstaben Sie verwenden, wenn Sie explizit sind. Wir hätten zum Beispiel a und b verwenden können, und es funktioniert genauso:
M = np.einsum('ab->ba', A)
Allerdings müssen Sie so viele Buchstaben angeben, wie Achsen im Operanden vorhanden sind. Da es in A zwei Achsen gibt, müssen Sie zwei unterschiedliche Buchstaben angeben. Das nächste Beispiel funktioniert nicht, da die Indexformel nur einen Buchstaben zu binden hat, i:
# broken
M = np.einsum('i->i', A)
Andererseits, wenn der Operand tatsächlich nur eine Achse hat (also ein Vektor), dann funktioniert die Formel mit dem Einzelbuchstaben-Index einwandfrei, obwohl sie nicht sehr nützlich ist, weil sie den Vektor a belässt wie es ist:
m = np.einsum('i->i', a)
Aber was ist mit dieser Operation? Auf der rechten Seite ist kein i. Ist das gültig?
c = np.einsum('i->', a)
Überraschenderweise ja!
Hier ist der erste Schlüssel zum Verständnis der Essenz von np.einsum: Wenn eine Achse auf der rechten Seite weggelassen wird, dann wird die Achse übersummiert.

Code:
c = 0 I = len(a) for i in range(I): c += a[i]
Das Summierverhalten ist nicht auf eine einzelne Achse beschränkt. Sie können beispielsweise über zwei Achsen gleichzeitig summieren, indem Sie diese tiefgestellte Formel verwenden: c = np.einsum('ij->', A):

Hier ist der entsprechende Python-Code für etwas über beide Achsen:
c = 0
I,J = A.shape
for i in range(I):
for j in range(J):
c += A[i,j]
Aber hier hört es noch nicht auf – wir können kreativ werden und einige Achsen zusammenfassen und andere in Ruhe lassen. Beispiel: np.einsum('ij->i', A) summiert die Zeilen der Matrix A und hinterlässt einen Vektor von Zeilensummen der Länge j:

Code:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
Ebenso summiert np.einsum('ij->j', A) Spalten in A.

Code:
M = np.einsum('ij->ji', A)
Es gibt eine Grenze für das, was wir mit einem einzelnen Operanden tun können. Mit zwei Operanden wird es viel interessanter (und nützlicher).
Nehmen wir an, Sie haben zwei Vektoren a = [a_1, a_2, ... ] und b = [a_1, a_2, ...].
Wenn len(a) === len(b), können wir das innere Produkt (auch Skalarprodukt genannt) wie folgt berechnen:
M = np.einsum('ab->ba', A)
Hier passieren zwei Dinge gleichzeitig:
Wenn man (1) und (2) zusammenfügt, erhält man das klassische innere Produkt.
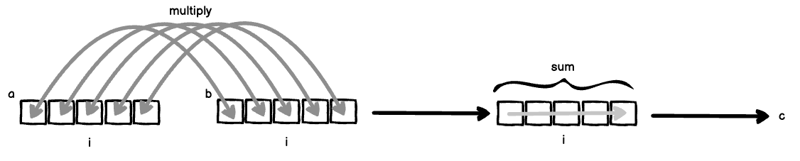
Code:
# broken
M = np.einsum('i->i', A)
Nehmen wir nun an, dass wir nicht i aus der Indexformel weggelassen haben, dann würden wir alle a[i] und b[i] multiplizieren und nicht über i summieren:
m = np.einsum('i->i', a)

Code:
c = np.einsum('i->', a)
Dies wird auch elementweise Multiplikation (oder das Hadamard-Produkt für Matrizen) genannt und erfolgt normalerweise über die Numpy-Methode np.multiply.
Es gibt noch eine dritte Variante der tiefgestellten Formel, die als äußeres Produkt bezeichnet wird.
c = 0 I = len(a) for i in range(I): c += a[i]
In dieser tiefgestellten Formel sind die Achsen von a und b an separate Buchstaben gebunden und werden daher als separate „Schleifenvariablen“ behandelt. Daher hat C Einträge a[i] * b[j] für alle i und j, angeordnet in einer Matrix.

Code:
c = 0
I,J = A.shape
for i in range(I):
for j in range(J):
c += A[i,j]
Um das äußere Produkt noch einen Schritt weiter zu gehen, finden Sie hier eine Version mit drei Operanden:
I,J = A.shape
r = np.zeros(I)
for i in range(I):
for j in range(J):
r[i] += A[i,j]

Der entsprechende Python-Code für unser äußeres Produkt mit drei Operanden ist:
I,J = A.shape
r = np.zeros(J)
for i in range(I):
for j in range(J):
r[j] += A[i,j]
Um noch weiter zu gehen, hindert uns nichts daran, die Achsen wegzulassen, um sie zu summieren, und zusätzlich das Ergebnis zu zu transponieren, indem wir auf der rechten Seite ki anstelle von ik schreiben ->:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
Der entsprechende Python-Code würde lauten:
M = np.einsum('ij->ji', A)
Jetzt hoffe ich, dass Sie beginnen können zu verstehen, wie Sie komplizierte Tensoroperationen ganz einfach spezifizieren können. Als ich intensiver mit Numpy arbeitete, griff ich jedes Mal nach np.einsum, wenn ich eine komplizierte Tensoroperation implementieren musste.
Meiner Erfahrung nach erleichtert np.einsum das spätere Lesen des Codes – ich kann die obige Operation direkt aus den Indizes ablesen: „Das äußere Produkt von drei Vektoren, wobei die Mittelachsen summiert werden und das Endergebnis transponiert wird.“ ". Wenn ich eine komplizierte Reihe von Numpy-Operationen lesen müsste, wäre ich möglicherweise sprachlos.
Lassen Sie uns als praktisches Beispiel die Gleichung im Herzen von LLMs aus dem klassischen Papier „Aufmerksamkeit ist alles, was Sie brauchen“ umsetzen.
Gl. 1 beschreibt den Aufmerksamkeitsmechanismus:

Wir werden unsere Aufmerksamkeit auf den Begriff richten QKT , weil Softmax nicht durch np.einsum und den Skalierungsfaktor berechenbar ist dk1 ist trivial anzuwenden.
Die QKT term stellt die Skalarprodukte von m Abfragen mit n Schlüsseln dar. Q ist eine Sammlung von m d-dimensionalen Zeilenvektoren, die in einer Matrix gestapelt sind, sodass Q die Form md hat. Ebenso ist K eine Sammlung von n d-dimensionalen Zeilenvektoren, die in einer Matrix gestapelt sind, sodass K die Form md hat.
Das Produkt zwischen einem einzelnen Q und K würde wie folgt geschrieben werden:
np.einsum('md,nd->mn', Q, K)
Beachten Sie, dass wir aufgrund der Art und Weise, wie wir unsere Indizesgleichung geschrieben haben, vermieden haben, K vor der Matrixmultiplikation transponieren zu müssen!

Das scheint also ziemlich einfach zu sein – tatsächlich handelt es sich lediglich um eine traditionelle Matrixmultiplikation. Allerdings sind wir noch nicht fertig. Aufmerksamkeit ist alles, was Sie brauchen verwendet Mehrkopfaufmerksamkeit, was bedeutet, dass wir wirklich k solcher Matrixmultiplikationen haben, die gleichzeitig über eine indizierte Sammlung von Q-Matrizen und K-Matrizen stattfinden .
Um die Sache etwas klarer zu machen, könnten wir das Produkt umschreiben als QiK iT .
Das bedeutet, dass wir sowohl für Q als auch für K eine zusätzliche Achse i haben.
Und darüber hinaus führen wir, wenn wir uns in einer Trainingsumgebung befinden, wahrscheinlich eine Serie solcher mehrköpfigen Aufmerksamkeitsoperationen durch.
Vermutlich würde ich die Operation über einen Stapel von Beispielen entlang einer Stapelachse b durchführen wollen. Das vollständige Produkt würde also etwa so aussehen:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
Ich werde das Diagramm hier überspringen, da es sich um 4-Achsen-Tensoren handelt. Aber vielleicht können Sie sich vorstellen, das frühere Diagramm zu „stapeln“, um unsere Mehrkopfachse i zu erhalten, und dann diese „Stapel“ zu „stapeln“, um unsere Stapelachse b zu erhalten.
Für mich ist es schwer vorstellbar, wie wir eine solche Operation mit einer beliebigen Kombination der anderen Numpy-Methoden implementieren würden. Doch mit ein wenig genauer Betrachtung ist klar, was passiert: Führen Sie über einen Stapel, über eine Sammlung von Matrizen Q und K, die Matrixmultiplikation Qt(K) durch.
Ist das nicht wunderbar?
Nachdem ich ein Jahr lang im Gründermodus gearbeitet habe, bin ich auf der Suche nach Arbeit. Ich verfüge über mehr als 15 Jahre Erfahrung in den unterschiedlichsten technischen Bereichen und Programmiersprachen und habe auch Erfahrung in der Leitung von Teams. Schwerpunkte sind Mathematik und Statistik. Schreib mir eine DM und lass uns reden!
Das obige ist der detaillierte Inhalt vonDer unvernünftige Nutzen von Numpys Einsum. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Verwendung der URL-Code-Funktion
Verwendung der URL-Code-Funktion
 Der Computer ist infiziert und kann nicht eingeschaltet werden
Der Computer ist infiziert und kann nicht eingeschaltet werden
 Die Leistung von Mikrocomputern hängt hauptsächlich davon ab
Die Leistung von Mikrocomputern hängt hauptsächlich davon ab
 So lösen Sie das Problem, dass Apple nicht mehr als 200 Dateien herunterladen kann
So lösen Sie das Problem, dass Apple nicht mehr als 200 Dateien herunterladen kann
 So geben Sie das Kleiner-gleich-Symbol in Windows ein
So geben Sie das Kleiner-gleich-Symbol in Windows ein
 So öffnen Sie ESP-Dateien
So öffnen Sie ESP-Dateien
 Software zur Erstellung von Sudoku-Lösern
Software zur Erstellung von Sudoku-Lösern
 Welche sind die am häufigsten verwendeten Bibliotheken in Golang?
Welche sind die am häufigsten verwendeten Bibliotheken in Golang?




