Merge-Sortieralgorithmus verstehen: Anfängerleitfaden zur Beherrschung des Sortieralgorithmus

In unseren vorherigen Artikeln haben wir eine ganze Reihe von Sortieralgorithmen wie Bubble Sort, Selection Sort und Insertion Sort kennengelernt. Wir haben gelernt, dass diese Sortieralgorithmen zwar sehr einfach zu implementieren sind, für große Datensätze jedoch nicht effizient sind, was bedeutet, dass wir einen effizienteren Algorithmus für die Sortierung großer Datensätze und damit für die Zusammenführungssortierung benötigen. In dieser Serie gehen wir darauf ein, wie die Zusammenführungssortierung funktioniert und wie sie in JavaScript implementiert werden kann. Bist du bereit?

Inhaltsverzeichnis

1. Was ist der Zusammenführungssortierungsalgorithmus?
2. So funktionieren Zusammenführungssortierungsalgorithmen
   • Zeitkomplexität
   • Weltraumkomplexität
3. Implementierung in JavaScript
4. Fazit

Was ist der Merge-Sort-Algorithmus?

Merge Sort Algorithm ist ein ausgezeichneter Sortieralgorithmus, der dem Divide-and-Conquer-Prinzip folgt. Im Gegensatz zu einfacheren Algorithmen wie Selection Sort und Bubble Sort, die mehrere Durchgänge durch das Array durchführen und benachbarte Elemente vergleichen, verfolgt Merge Sort einen strategischeren Ansatz:

1. Teilen: Zuerst teilt Merge Sort das Array in zwei Hälften
2. Erobern: Zweitens wird jede Hälfte rekursiv sortiert
3. Kombinieren: Zum Schluss werden die sortierten Hälften wieder zusammengefügt

Dieser Ansatz übertrifft durchweg einfachere O(n²)-Algorithmen wie Selection Sort und Bubble Sort, wenn es um größere Datensätze geht.

So funktionieren Zusammenführungssortierungsalgorithmen

Wir haben gesehen, dass die Zusammenführungssortierung mithilfe des beliebten Divide-and-Conquer-Ansatzes funktioniert. Unten finden Sie eine visuelle Darstellung der Funktionsweise.

Da wir nun die Magie gesehen haben, gehen wir durch die Funktionsweise des Merge-Sort-Algorithmus, indem wir dieses Array manuell sortieren: [38, 27, 43, 3, 9, 82, 10] mit dem oben genannten Ansatz.

Schritt 1: Teilen

Der erste Schritt bei der Zusammenführungssortierung besteht darin, das Array in Unterarrays zu unterteilen und dann jedes Unterarray in Unterarrays und das Unterarray in Unterarrays zu unterteilen, bis in allen Unterarrays nur noch ein Element übrig ist.

Schritt 2: Zurückverschmelzen (Erobern)

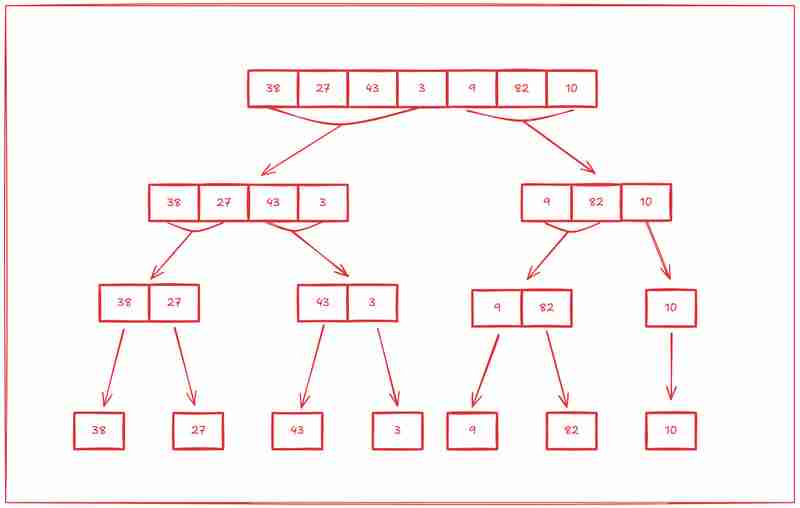
Der zweite Schritt besteht darin, mit dem Sortieren dieser Subarrays von Grund auf zu beginnen.

Zeitkomplexität

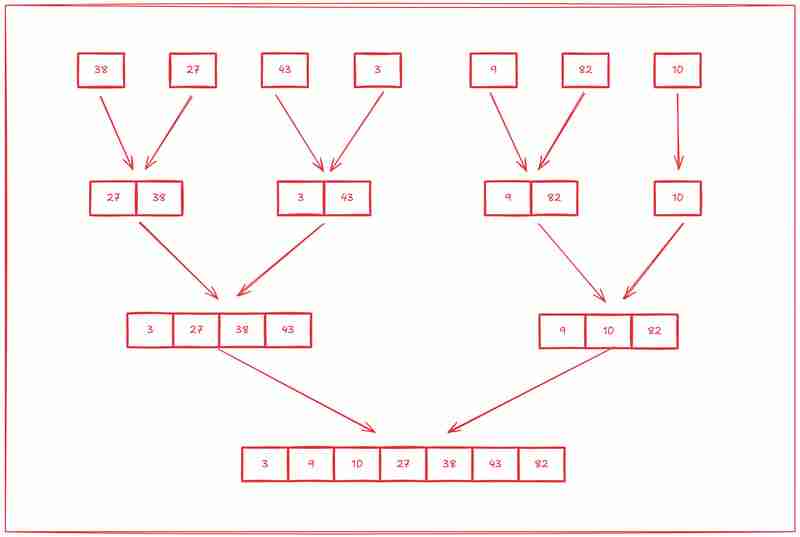
Merge Sort erreicht in allen Fällen (beste, mittlere und schlechteste) Zeitkomplexität von O(n log n) und ist damit für größere Datensätze effizienter als O(n²)-Algorithmen.

Hier ist der Grund:

• Dividieren: Das Array wird logarithmisch n-mal geteilt (jede Division halbiert die Größe)
• Zusammenführen: Jede Zusammenführungsebene erfordert n Operationen
• Gesamt: n Operationen × log n Ebenen = O(n log n)

Vergleichen Sie dies mit:

• Blasensortierung: O(n²)
• Auswahlsortierung: O(n²)
• Zusammenführungssortierung: O(n log n)

Für ein Array von 1.000 Elementen:

• O(n²) ≈ 1.000.000 Operationen
• O(n log n) ≈ 10.000 Operationen

Weltraumkomplexität

Merge Sort erfordert O(n) zusätzlichen Speicherplatz, um die temporären Arrays während des Zusammenführens zu speichern. Dies ist zwar mehr als der von Bubble Sort oder Selection Sort benötigte O(1)-Platz, aber die Zeiteffizienz macht diesen Kompromiss in der Praxis normalerweise lohnenswert.

Implementierung in JavaScript

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

Aufschlüsselung der Zusammenführungsfunktion:

1. Funktionseinrichtung:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

• Erstellt ein leeres Array zum Speichern zusammengeführter Ergebnisse
• Initialisiert Zeiger für beide Eingabearrays
• Stellen Sie sich diese Zeiger wie Finger vor, die verfolgen, wo wir uns in jedem Array befinden

1. Hauptzusammenführungslogik:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

• Vergleicht Elemente aus beiden Arrays
• Nimmt das kleinere Element und fügt es dem Ergebnis hinzu
• Bewegt den Zeiger in dem Array, aus dem wir entnommen haben, vorwärts
• Als würde man beim Sortieren eines Stapels die kleinere von zwei Karten wählen

1. Aufräumphase:

   while (leftIndex < left.length) {
     result.push(left[leftIndex]);
     leftIndex++;
   }

• Fügt alle verbleibenden Elemente hinzu
• Notwendig, da ein Array möglicherweise länger ist als das andere
• Als würde man die restlichen Karten nach dem Vergleich einsammeln

Die Hauptfunktion zum Zusammenführen und Sortieren

function mergeSort(arr) {
  // Base case
  if (arr.length <= 1) {
    return arr;
  }

  // Divide
  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // Conquer and Combine
  return merge(mergeSort(left), mergeSort(right));
}

MergeSort aufschlüsseln:

1. Basisfall:

   if (arr.length <= 1) {
     return arr;
   }

• Verarbeitet Arrays der Länge 0 oder 1
• Diese sind bereits nach Definition sortiert
• Dient als unser Rekursionsstopppunkt

1. Teilungsphase:

   const middle = Math.floor(arr.length / 2);
   const left = arr.slice(0, middle);
   const right = arr.slice(middle);

• Teilt das Array in zwei Hälften
• Slice() erstellt neue Arrays, ohne das Original zu ändern
• Als würde man ein Kartenspiel in zwei Hälften schneiden

1. Rekursives Sortieren und Zusammenführen:

   return merge(mergeSort(left), mergeSort(right));

• Sortiert jede Hälfte rekursiv
• Kombiniert sortierte Hälften mithilfe der Zusammenführungsfunktion
• Zum Beispiel kleinere Kartenstapel zu sortieren, bevor man sie kombiniert

Beispiel-Komplettlösung

Mal sehen, wie es sortiert wird [38, 27, 43, 3]:

1. Erster Split:

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

1. Zweiter Split:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

1. Zurück zusammenführen:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

Abschluss

Merge Sort zeichnet sich durch einen hocheffizienten Sortieralgorithmus aus, der bei großen Datensätzen stets eine gute Leistung erbringt. Obwohl es im Vergleich zu einfacheren Sortieralgorithmen zusätzlichen Platz benötigt, ist es aufgrund seiner O(n log n)-Zeitkomplexität eine erste Wahl für viele reale Anwendungen, bei denen die Leistung entscheidend ist.

Wichtige Erkenntnisse:

• Verwendet die Divide-and-Conquer-Strategie
• O(n log n) Zeitkomplexität in allen Fällen
• Benötigt O(n) zusätzlichen Platz
• Stabiler Sortieralgorithmus
• Hervorragend geeignet für große Datensätze

---

---

Bleiben Sie auf dem Laufenden und verbunden

Um sicherzustellen, dass Sie keinen Teil dieser Serie verpassen und um mit mir in Kontakt zu treten, um mehr darüber zu erfahren
Diskussionen über Softwareentwicklung (Web, Server, Mobil oder Scraping/Automatisierung), Daten
Strukturen und Algorithmen und andere spannende Technologiethemen, folgen Sie mir auf:

Emmanuel Ayinde Folgen

Softwareentwickler | Technischer Redakteur | Backend-, Web- und Mobilentwickler? | Leidenschaft für die Entwicklung effizienter und skalierbarer Softwarelösungen. #letsconnect ?

• GitHub
• Linkedin
• X (Twitter)

Bleiben Sie dran und viel Spaß beim Programmieren ?‍??

Das obige ist der detaillierte Inhalt vonMerge-Sortieralgorithmus verstehen: Anfängerleitfaden zur Beherrschung des Sortieralgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!