Untersuchung der Leistung von np.einsum

Ein Leser meines letzten Blogbeitrags hat mich darauf hingewiesen, dass np.einsum für scheibenweise Matmul-ähnliche Operationen erheblich langsamer ist als np.matmul, es sei denn, Sie aktivieren das Optimierungsflag in der Parameterliste: np.einsum(.. ., optimieren = True).

Da ich etwas skeptisch war, startete ich ein Jupyter-Notebook und führte einige Vorversuche durch. Und ich will verdammt sein, es ist völlig wahr – selbst für Fälle mit zwei Operanden, bei denen die Optimierung überhaupt keinen Unterschied machen sollte!

Test 1 ist ziemlich einfach – Matrixmultiplikation zweier Matrizen der C-Ordnung (auch bekannt als Zeilenhauptordnung) unterschiedlicher Dimensionen. np.matmul ist durchweg etwa zwanzigmal schneller.

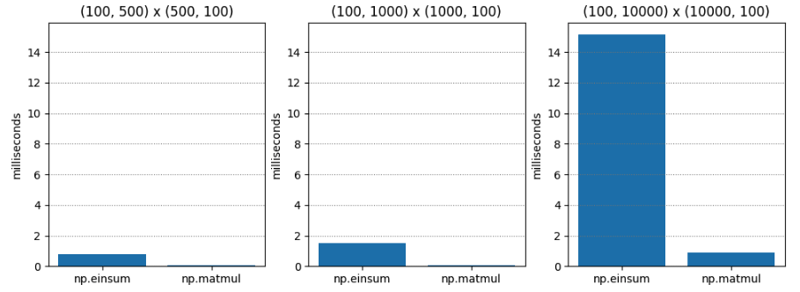
M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.765	0.045	17.055
(100, 1000)	(1000, 100)	1.495	0.073	20.554
(100, 10000)	(10000, 100)	15.148	0.896	16.899

Für Test 2 mit „optimize=True“ unterscheiden sich die Ergebnisse drastisch. np.einsum ist immer noch langsamer, aber im schlimmsten Fall nur etwa 1,5-mal langsamer!

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.063	0.043	1.474
(100, 1000)	(1000, 100)	0.086	0.067	1.284
(100, 10000)	(10000, 100)	1.000	0.936	1.068

Warum?

Mein Verständnis des Optimierungsflags ist, dass es eine optimale Kontraktionsreihenfolge bestimmt, wenn drei oder mehr Operanden vorhanden sind. Hier haben wir nur zwei Operanden. Eine Optimierung sollte also keinen Unterschied machen, oder?

Aber vielleicht bedeutet Optimieren mehr als nur die Auswahl einer Kontraktionsreihenfolge? Vielleicht ist sich die Optimierung des Speicherlayouts bewusst, und das hat etwas mit dem zeilen- und spaltenorientierten Layout zu tun?

Bei der Grundschulmethode der Matrixmultiplikation iterieren Sie zum Berechnen eines einzelnen Eintrags über eine Zeile in op1, während Sie über eine Spalte in op2 iterieren. Wenn Sie also das zweite Argument in der Hauptspaltenreihenfolge anordnen, kann dies zu einer Beschleunigung führen für np.einsum (vorausgesetzt, dass np.einsum eine Art verallgemeinerte Version der Grundschulmethode der Matrixmultiplikation unter der Haube ist, was meiner Meinung nach wahr ist).

Also habe ich für Test 3 eine Spaltenhauptmatrix für den zweiten Operanden übergeben, um zu sehen, ob dies np.einsum beschleunigt, wenn Optimize=False.

Hier sind die Ergebnisse. Überraschenderweise ist np.einsum immer noch erheblich schlechter. Offensichtlich passiert etwas, das ich nicht verstehe – vielleicht verwendet np.einsum einen völlig anderen Codepfad, wenn „Optimize“ auf „True“ gesetzt ist? Zeit, mit dem Graben zu beginnen.

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	1.486	0.056	26.541
(100, 1000)	(1000, 100)	3.885	0.125	31.070
(100, 10000)	(10000, 100)	49.669	1.047	47.444

Tiefer gehen

In den Versionshinweisen von Numpy 1.12.0 wird die Einführung des Optimierungsflags erwähnt. Der Zweck von „Optimize“ scheint jedoch darin zu bestehen, die Reihenfolge zu bestimmen, in der Argumente in einer Operandenkette kombiniert werden (d. h. die Assoziativität) – „Optimize“ sollte also keinen Unterschied für nur zwei Operanden machen, oder? Hier sind die Versionshinweise:

np.einsum unterstützt jetzt das Optimierungsargument, das die Kontraktionsreihenfolge optimiert. Zum Beispiel würde np.einsum den Kettenpunktbeispiel np.einsum(‘ij,jk,kl->il’, a, b, c) in einem einzigen Durchgang vervollständigen, der wie N^4 skaliert würde; Wenn jedoch „optimize=True“ ist, erstellt np.einsum ein Zwischenarray, um diese Skalierung auf N^3 oder effektiv np.dot(a, b).dot(c) zu reduzieren. Die Verwendung von Zwischentensoren zur Reduzierung der Skalierung wurde auf die allgemeine Einsum-Summennotation angewendet. Weitere Informationen finden Sie unter np.einsum_path.

Um das Rätsel noch zu verschlimmern, weisen einige spätere Versionshinweise darauf hin, dass np.einsum aktualisiert wurde, um Tensordot zu verwenden (das selbst ggf. BLAS verwendet). Das scheint vielversprechend.

Aber warum sehen wir dann nur die Beschleunigung, wenn die Optimierung wahr ist? Was ist los?

Wenn wir def einsum(*operands, out=None, optimieren=False, **kwargs) in numpy/numpy/_core/einsumfunc.py lesen, kommen wir fast sofort zu dieser Early-out-Logik:

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

Verwendet c_einsum Tensordot? Ich bezweifle es. Später im Code sehen wir den Tensordot-Aufruf, auf den sich die 1.14-Notizen zu beziehen scheinen:

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

Also, hier ist was passiert:

1. Die Kontraktionsliste-Schleife wird ausgeführt, wenn „optimieren“ „True“ ist – selbst im trivialen Fall mit zwei Operanden.
2. tensordot wird nur in der Kontraktionsliste-Schleife aufgerufen.
3. Daher rufen wir Tensordot (und damit BLAS) auf, wenn „Optimize“ True ist.

Für mich scheint das ein Fehler zu sein. Meiner Meinung nach sollte das „Early-Out“ am Anfang von np.einsum immer noch erkennen, ob die Operanden Tensordot-kompatibel sind, und wenn möglich Tensordot aufrufen. Dann würden wir die offensichtlichen BLAS-Beschleunigungen erhalten, selbst wenn „Optimize“ auf „False“ gesetzt ist. Schließlich bezieht sich die Semantik von „Optimize“ auf die Kontraktionsreihenfolge und nicht auf die Verwendung von BLAS, was meiner Meinung nach eine Selbstverständlichkeit sein sollte.

Der Vorteil hierbei ist, dass Personen, die np.einsum für Vorgänge aufrufen, die einem Tensordot-Aufruf entsprechen, die entsprechenden Beschleunigungen erhalten, was np.einsum aus Leistungssicht etwas weniger gefährlich macht.

Wie funktioniert c_einsum eigentlich?

Ich habe ein wenig C-Code geschrieben, um es mir anzusehen. Das Herzstück der Umsetzung ist hier.

Nach ausführlicher Argumentanalyse und Parametervorbereitung wird die Achseniterationsreihenfolge bestimmt und ein spezieller Iterator vorbereitet. Jeder Ertrag des Iterators stellt eine andere Möglichkeit dar, alle Operanden gleichzeitig zu durchlaufen.

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

Unter der Annahme, dass bestimmte Sonderfalloptimierungen nicht anwendbar sind, wird eine geeignete Produktsummenfunktion (SOP) basierend auf den beteiligten Datentypen bestimmt:

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

Und dann wird diese SOP-Operation (Summe der Produkte) bei jedem Multioperandenschritt aufgerufen, der vom Iterator zurückgegeben wird, wie hier zu sehen:

    /* Allocate the iterator */
    iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
                               op_dtypes, ndim_iter, op_axes, NULL, 0);

Das ist mein Verständnis von der Funktionsweise von Einsum, das zugegebenermaßen noch etwas dürftig ist – es verdient wirklich mehr als die Stunde, die ich ihm gewidmet habe.

Aber es bestätigt meine Vermutungen, dass es sich wie eine verallgemeinerte Gigabrain-Version der Grundschulmethode der Matrixmultiplikation verhält. Letztendlich wird es an eine Reihe von „Produktsummen“-Operationen delegiert, die auf „Läufern“ beruhen, die sich durch die Operanden bewegen – nicht allzu verschieden von dem, was Sie mit Ihren Fingern tun, wenn Sie die Matrixmultiplikation lernen.

Zusammenfassung

Warum ist np.einsum im Allgemeinen schneller, wenn Sie es mit „optimize=True“ aufrufen? Dafür gibt es zwei Gründe.

Der erste (und ursprüngliche) Grund besteht darin, dass versucht wird, einen optimalen Kontraktionspfad zu finden. Wie ich jedoch bereits betont habe, sollte das keine Rolle spielen, wenn wir nur zwei Operanden haben, wie wir es in unseren Leistungstests tun.

Der zweite (und neuere) Grund ist, dass bei „optimize=True“ auch im Zwei-Operanden-Fall ein Codepfad aktiviert wird, der nach Möglichkeit Tensordot aufruft, das wiederum versucht, BLAS zu verwenden. Und BLAS ist so optimiert wie die Matrixmultiplikation nur sein kann!

Das Rätsel um die Beschleunigung durch zwei Operanden ist also gelöst! Allerdings haben wir die Merkmale der Beschleunigung aufgrund der Kontraktionsreihenfolge nicht wirklich behandelt. Das muss auf einen zukünftigen Beitrag warten! Bleiben Sie dran!

Das obige ist der detaillierte Inhalt vonUntersuchung der Leistung von np.einsum. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!