kann die Fläche unter einer Kurve berechnen
Kann Excel die Fläche unter einer Kurve berechnen?
Ja, Excel kann die Fläche unter einer Kurve mithilfe der Trapezregel oder der Simpson-Regel berechnen.
Wie berechnet Excel die Fläche unter einer Kurve?
Trapezförmig Regel
- Teilen Sie die Kurve in Trapeze, indem Sie die Grenzen definieren.
- Berechnen Sie die Fläche jedes Trapezes mit der Formel:
Area = (b2 - b1) * h / 2, wobeib1undb2die sind Basen undhist die Höhe. - Summieren Sie die Flächen aller Trapeze, um die zu erhalten Gesamtfläche unter der Kurve.
Simpson-Regel
- Ähnlich der Trapezregel, aber sie unterteilt die Kurve in parabolische Segmente.
- Berechnen Sie die Fläche jedes Parabelsegments mithilfe der Formel:
Area = (b2 - b1) * (h/6) * (f(b1) 4f(c) f(b2)), wobeicder Mittelpunkt dazwischen istb1undb2. - Summieren Sie die Flächen aller Parabelsegmente, um die Gesamtfläche unter der Kurve zu erhalten.
Kann Excel die Fläche unter einer komplexen Kurve genau berechnen? ?
Ja, Excel kann die Fläche unter einer komplexen Kurve genau berechnen, wenn die Kurve ein gutes Verhalten aufweist (glatt und kontinuierlich). Sowohl die Trapezregel als auch die Simpson-Regel liefern vernünftige Näherungen. Allerdings:
- Die Genauigkeit wird durch die Anzahl der verwendeten Teilintervalle beeinflusst.
- Für Kurven mit starken Änderungen oder Diskontinuitäten können für eine höhere Genauigkeit mehr Teilintervalle erforderlich sein.
- Die Trapezregel neigt dazu, die Fläche zu unterschätzen, während die Simpson-Regel sie überschätzt.
- Für hoch Für nichtlineare Kurven sind möglicherweise andere Methoden wie die numerische Integration mit Gauss-Legendre-Quadratur besser geeignet.
Das obige ist der detaillierte Inhalt vonkann die Fläche unter einer Kurve berechnen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1676
1676
 14
14
 1429
1429
 52
52
 1333
1333
 25
25
 1278
1278
 29
29
 1257
1257
 24
24
 Wenn Sie Tische in Excel nicht umbenennen
Apr 15, 2025 am 12:58 AM
Wenn Sie Tische in Excel nicht umbenennen
Apr 15, 2025 am 12:58 AM
Schneller Link Warum sollten Tabellen in Excel genannt werden? So nennen Sie eine Tabelle in Excel Excel -Tabellen -Benennungsregeln und -techniken Standardmäßig werden Tabellen in Excel als Tabelle 1, Tabelle 2, Tabelle 3 usw. bezeichnet. Sie müssen sich jedoch nicht an diese Tags halten. Tatsächlich wäre es besser, wenn Sie es nicht tun würden! In diesem schnellen Leitfaden werde ich erklären, warum Sie Tische immer in Excel umbenennen und Ihnen zeigen sollten, wie das geht. Warum sollten Tabellen in Excel genannt werden? Während es einige Zeit dauern kann, die Gewohnheit zu entwickeln, Tabellen in Excel zu benennen (wenn Sie dies normalerweise nicht tun), veranschaulichen die folgenden Gründe heute
 So ändern Sie Excel -Tabellenstile und entfernen Sie die Tabellenformatierung
Apr 19, 2025 am 11:45 AM
So ändern Sie Excel -Tabellenstile und entfernen Sie die Tabellenformatierung
Apr 19, 2025 am 11:45 AM
In diesem Tutorial werden Sie Excel -Tabellenstile anwenden, modifizieren und entfernen, während Sie alle Tabellenfunktionen erhalten. Möchten Sie Ihre Excel -Tische genau so aussehen, wie Sie es wollen? Lesen Sie weiter! Nach dem Erstellen einer Excel -Tabelle ist der erste Schritt üblich
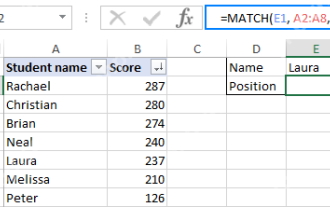 Excel -Match -Funktion mit Formel -Beispielen
Apr 15, 2025 am 11:21 AM
Excel -Match -Funktion mit Formel -Beispielen
Apr 15, 2025 am 11:21 AM
In diesem Tutorial wird erläutert, wie die Übereinstimmungsfunktion in Excel mit Formel -Beispielen verwendet wird. Es zeigt auch, wie Sie Ihre Lookup -Formeln verbessern können, indem Sie eine dynamische Formel mit Vlookup und Übereinstimmung erstellen. In Microsoft Excel gibt es viele verschiedene Lookups/Refs
 So machen Sie Ihre Excel -Tabelle für alle zugänglich
Apr 18, 2025 am 01:06 AM
So machen Sie Ihre Excel -Tabelle für alle zugänglich
Apr 18, 2025 am 01:06 AM
Verbessern Sie die Zugänglichkeit von Excel -Tabellen: ein praktischer Leitfaden Machen Sie beim Erstellen eines Microsoft Excel -Arbeitsbuchs unbedingt die erforderlichen Schritte, um sicherzustellen, dass jeder Zugriff darauf hat, insbesondere wenn Sie die Arbeitsmappe mit anderen teilen möchten. Dieser Leitfaden gibt einige praktische Tipps, um dies zu erreichen. Verwenden Sie einen beschreibenden Arbeitsblattamen Eine Möglichkeit, die Zugänglichkeit von Excel -Arbeitsmappen zu verbessern, besteht darin, den Namen des Arbeitsblatts zu ändern. Standardmäßig werden Excel-Arbeitsblätter mit dem Namen Sheet1, Sheet2, Sheet3 usw. bezeichnet. Dieses nicht deeskriptive Nummerierungssystem wird fortgesetzt, wenn Sie auf "" klicken, um ein neues Arbeitsblatt hinzuzufügen. Das Ändern des Arbeitsblattsnamens hat mehrere Vorteile, um den Arbeitsblattinhalt genauer zu beschreiben: tragen
 Ignorieren Sie die Leistung von F4 in Microsoft Excel nicht
Apr 24, 2025 am 06:07 AM
Ignorieren Sie die Leistung von F4 in Microsoft Excel nicht
Apr 24, 2025 am 06:07 AM
Ein Muss für Excel-Experten: Der wunderbare Gebrauch des F4-Schlüssels, eine Geheimwaffe, um die Effizienz zu verbessern! In diesem Artikel werden die leistungsstarken Funktionen des F4 -Schlüssels in Microsoft Excel unter Windows -System angezeigt, wodurch Sie diesen Abkürzungschlüssel schnell beherrschen, um die Produktivität zu verbessern. 1.. Referenztyp des Formelschalters umschalten Zu den Referenztypen in Excel gehören relative Referenzen, absolute Referenzen und gemischte Referenzen. Die F4 -Tasten können zwischen diesen Typen bequem umgeschaltet werden, insbesondere beim Erstellen von Formeln. Angenommen, Sie müssen den Preis von sieben Produkten berechnen und eine Steuern von 20% hinzufügen. In Zelle E2 können Sie die folgende Formel eingeben: = Sum (d2 (d2*a2)) Nach der Eingabe der Eingabe kann der Preis von 20% berechnet werden. Aber,
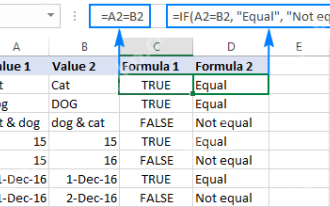 Excel: Vergleiche Saiten in zwei Zellen für Übereinstimmungen (Fall-unempfindlich oder genau)
Apr 16, 2025 am 11:26 AM
Excel: Vergleiche Saiten in zwei Zellen für Übereinstimmungen (Fall-unempfindlich oder genau)
Apr 16, 2025 am 11:26 AM
Das Tutorial zeigt, wie Textsaiten in Excel für Fall-unempfindliche und genaue Übereinstimmung verglichen werden. Sie lernen eine Reihe von Formeln, um zwei Zellen nach ihren Werten, der Stringlänge oder der Anzahl der Vorkommen eines bestimmten Zeichens zu vergleichen, a
 5 Open-Source-Alternativen zu Microsoft Excel
Apr 16, 2025 am 12:56 AM
5 Open-Source-Alternativen zu Microsoft Excel
Apr 16, 2025 am 12:56 AM
Excel bleibt in der Geschäftswelt dank der vertrauten Schnittstellen, Datenwerkzeuge und einer Vielzahl von Funktionssätzen beliebt. Open -Source -Alternativen wie Libreoffice Calc und Gnumeric sind mit Excel -Dateien kompatibel. NurOffice und Grist bieten Cloud-basierte Tabellenkalkulations-Redakteure mit Kollaborationsfunktionen. Auf der Suche nach Open -Source -Alternativen zu Microsoft Excel hängt davon ab, was Sie erreichen möchten: Verfolgen Sie Ihre monatliche Einkaufsliste oder suchen Sie nach Tools, die Ihre Geschäftsprozesse unterstützen können? Hier finden Sie einige Tabellenkalkulationsredakteure für eine Vielzahl von Anwendungsfällen. Excel bleibt ein Riese in der Geschäftswelt Microsoft Ex
 Ich benenne immer in Excel Bereiche, und du solltest auch
Apr 19, 2025 am 12:56 AM
Ich benenne immer in Excel Bereiche, und du solltest auch
Apr 19, 2025 am 12:56 AM
Verbesserung der Excel -Effizienz: Nutzen Sie die benannten Regionen gut Standardmäßig sind Microsoft Excel-Zellen nach Spaltenreihenkoordinaten wie A1 oder B2 benannt. Sie können jedoch Zellen oder Zellbereichen spezifischere Namen zuweisen, um die Navigation zu verbessern, Formeln klarer zu machen und letztendlich Zeit zu sparen. Warum Regionen in Excel immer benennen? Möglicherweise sind Sie mit Lesezeichen in Microsoft Word vertraut, bei denen es sich um unsichtbare Wegweiser für die angegebenen Standorte in Ihrem Dokument handelt, und Sie können jederzeit dorthin springen, wo Sie möchten. Microsoft Excel verfügt über eine unbegründete Alternative zu diesem zeitsparenden Tool namens "Namen" und ist über die Namensbox in der oberen linken Ecke der Arbeitsmappe zugänglich. Verwandte Inhalt #




