不知道大家对DES有没有兴趣,今天在整理的时候,看到我在一年半前翻译的一篇文章。
如何实现 DES 算法(全)。
这是摘自清华BBS的一篇文章,洋文的,小弟把它翻成中文请各位高手指点。
分号(;)后的话是小弟的翻译,井号(#)后的是小弟的一点感想。
How to implement the
Data Encryption Standard (DES)
A step by step tutorial
Version 1.2
The Data Encryption Standard (DES) algorithm, adopted by the U.S.
government in 1977, is a block cipher that transforms 64-bit data blocks
under a 56-bit secret key, by means of permutation and substitution. It
is officially described in FIPS PUB 46. The DES algorithm is used for
many applications within the government and in the private sector.
This is a tutorial designed to be clear and compact, and to provide a
newcomer to the DES with all the necessary information to implement it
himself, without having to track down printed works or wade through C
source code. I welcome any comments.
Matthew Fischer
;上面是介绍,我就不翻了。 ;)
Here's how to do it, step by step:
1 Process the key.
;生成密钥
1.1 Get a 64-bit key from the user. (Every 8th bit is considered a
parity bit. For a key to have correct parity, each byte should contain
an odd number of "1" bits.)
;从用户处得到一个64位的密钥。(每8位一组,每组的第8位是校验位。如果校验
正确,每个字节应该有一个为1的
1.2 Calculate the key schedule.
;计算密钥表
1.2.1 Perform the following permutation on the 64-bit key. (The parity
bits are discarded, reducing the key to 56 bits. Bit 1 of the permuted
block is bit 57 of the original key, bit 2 is bit 49, and so on with bit
56 being bit 4 of the original key.)
;对64位的密钥进行如下的置换。(去掉校验位,密钥的实际长度是56位。置换后的
;第一位是原密钥的第57位,第二位是原第49位,第五十六位就是原来密钥的第4位。)
# 古怪的置换,哪位大哥能写出算式?
# 好象是分成两部
# for(j=57;j# {
# for(i=j;i# {
# if(k=28)
# break;
# c[k]=i;
# k++;
# }
# 这是前28位,不知道对不对?请指正。
Permuted Choice 1 (PC-1)
57 49 41 33 25 17 9
1 58 50 42 34 26 18
10 2 59 51 43 35 27
19 11 3 60 52 44 36
63 55 47 39 31 23 15
7 62 54 46 38 30 22
14 6 61 53 45 37 29
21 13 5 28 20 12 4
1.2.2 Split the permuted key into two halves. The first 28 bits are
called C[0] and the last 28 bits are called D[0].
;把置换后的密钥分为C[0] 和D[0]两部分,各28位。
1.2.3 Calculate the 16 subkeys. Start with i = 1.
;计算16个子密钥,从i=1开始。
1.2.3.1 Perform one or two circular left shifts on both C[i-1] and
D[i-1] to get C[i] and D[i], respectively. The number of shifts per
iteration are given in the table below.
;分别对C[i-1]和D[i-1]进行左移一到两位的位移操作,得到C[i]和D[i]。每次
;位移数目如下:
# 共16次
Iteration # 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Left Shifts 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
1.2.3.2 Permute the concatenation C[i]D[i] as indicated below. This
will yield K[i], which is 48 bits long.
;如下表,改变C[i]和D[i]的排列,得到48位长的k[i]。
# 不懂 :(
# 是不是丢掉了某些位?
Permuted Choice 2 (PC-2)
14 17 11 24 1 5
3 28 15 6 21 10
23 19 12 4 26 8
16 7 27 20 13 2
41 52 31 37 47 55
30 40 51 45 33 48
44 49 39 56 34 53
46 42 50 36 29 32
1.2.3.3 Loop back to 1.2.3.1 until K[16] has been calculated.
;重复 1.2.3.1 开始的过程,算出16个字密钥。
2 Process a 64-bit data block.
;处理一个64位的数据块。
2.1 Get a 64-bit data block. If the block is shorter than 64 bits, it
should be padded as appropriate for the application.
;获取一个64位的数据块。如果数据块不到64位,就补足64位。
# 可能是用0补吧。
2.2 Perform the following permutation on the data block.
;对数据块进行如下置换。
# 又是分成两部分进行,先是偶数位。
# 比较简单,算式就不写了。
Initial Permutation (IP)
58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7
2.3 Split the block into two halves. The first 32 bits are called L[0],
and the last 32 bits are called R[0].
;将数据块平分为L[0]和R[0]两部分。
2.4 Apply the 16 subkeys to the data block. Start with i = 1.
;从i=1开始,用16个子密钥对数据块进行加密。
2.4.1 Expand the 32-bit R[i-1] into 48 bits according to the
bit-selection function below.
;将数据块的后32位R[i-1]以下面规则进行扩展。
# 不会写算式。:(
Expansion (E)
32 1 2 3 4 5
4 5 6 7 8 9
8 9 10 11 12 13
12 13 14 15 16 17
16 17 18 19 20 21
20 21 22 23 24 25
24 25 26 27 28 29
28 29 30 31 32 1
2.4.2 Exclusive-or E(R[i-1]) with K[i].
;用K[i]对E(R[i-1])进行异或操作。
2.4.3 Break E(R[i-1]) xor K[i] into eight 6-bit blocks. Bits 1-6 are
B[1], bits 7-12 are B[2], and so on with bits 43-48 being B[8].
;将上一步的操作结果分成8块,每块6位,命名为B[1]到B[8]。
2.4.4 Substitute the values found in the S-boxes for all B[j]. Start
with j = 1. All values in the S-boxes should be considered 4 bits wide.
;把所有的B[j]在S框中进行置换,S框中所有的值的宽(长)度应是4位。
# 不懂!!! :(
2.4.4.1 Take the 1st and 6th bits of B[j] together as a 2-bit value
(call it m) indicating the row in S[j] to look in for the substitution.
;把B[j]中的第一位和第六位命名为m,表示S[j]在置换时的行。
2.4.4.2 Take the 2nd through 5th bits of B[j] together as a 4-bit
value (call it n) indicating the column in S[j] to find the substitution.
;把B[j]二到五位命名为n,表示S[j]在置换时的列。
2.4.4.3 Replace B[j] with S[j][m][n].
;用S[j][m][n]置换B[j]。
Substitution Box 1 (S[1])
14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7
0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8
4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0
15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13
S[2]
15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10
3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5
0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15
13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9
S[3]
10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8
13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1
13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7
1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12
S[4]
7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15
13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9
10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4
3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14
S[5]
2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9
14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6
4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14
11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3
S[6]
12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11
10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8
9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6
4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13
S[7]
4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1
13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6
1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2
6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12
S[8]
13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7
1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2
7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8
2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
2.4.4.4 Loop back to 2.4.4.1 until all 8 blocks have been replaced.
;重复2.4.4.1开始的步骤,直至8个数据块都被置换。
2.4.5 Permute the concatenation of B[1] through B[8] as indicated below.
;以下面的方法改变B[1]到B[8]的顺序 。
Permutation P
16 7 20 21
29 12 28 17
1 15 23 26
5 18 31 10
2 8 24 14
32 27 3 9
19 13 30 6
22 11 4 25
2.4.6 Exclusive-or the resulting value with L[i-1]. Thus, all together,
your R[i] = L[i-1] xor P(S[1](B[1])...S[8](B[8])), where B[j] is a 6-bit
block of E(R[i-1]) xor K[i]. (The function for R[i] is written as, R[i] =
L[i-1] xor f(R[i-1], K[i]).)
;用L[i-1]对上一步的结果进行异或操作。如此就有以下结果:R[i] = L[i-1] xor ;
P(S[1](B[1])...S[8](B[8]))。这里,B[j]是六位的数据块,它是E(R[i-1]) xor
;K[i]的结果。(R[i]的函数可以写成R[i] = L[i-1] xor f(R[i-1], K[i])。)
2.4.7 L[i] = R[i-1].
;L[i] = R[i-1].
2.4.8 Loop back to 2.4.1 until K[16] has been applied.
;重复2.4.1开始的步骤,直至所有的子密钥都被使用过。
# 就是再重复15次,每次使用不同的子密钥。
2.5 Perform the following permutation on the block R[16]L[16].
;对R[16]L[16]进行如下的置换。
Final Permutation (IP**-1)
40 8 48 16 56 24 64 32
39 7 47 15 55 23 63 31
38 6 46 14 54 22 62 30
37 5 45 13 53 21 61 29
36 4 44 12 52 20 60 28
35 3 43 11 51 19 59 27
34 2 42 10 50 18 58 26
33 1 41 9 49 17 57 25
This has been a description of how to use the DES algorithm to encrypt
one 64-bit block. To decrypt, use the same process, but just use the keys
K[i] in reverse order. That is, instead of applying K[1] for the first
iteration, apply K[16], and then K[15] for the second, on down to K[1].
;以上就是怎样用DES算法对一个64位的数据块进行加密的过程。至于解密,只需要
;在以上过程中把子密钥的顺序倒过来用就可以了。也就是说,在加密时用子密钥
;K[1],在解密过程中就用K[16];在加密时用子密钥K[2],在解密过程中就用K[12]。
Summaries:
;摘要
# 以下是生成子密钥,加密和解密的公式化叙述。
Key schedule:
C[0]D[0] = PC1(key)
for 1 C[i] = LS[i](C[i-1])
D[i] = LS[i](D[i-1])
K[i] = PC2(C[i]D[i])
Encipherment:
L[0]R[0] = IP(plain block)
for 1 L[i] = R[i-1]
R[i] = L[i-1] xor f(R[i-1], K[i])
cipher block = FP(R[16]L[16])
Decipherment:
R[16]L[16] = IP(cipher block)
for 1 R[i-1] = L[i]
L[i-1] = R[i] xor f(L[i], K[i])
plain block = FP(L[0]R[0])
To encrypt or decrypt more than 64 bits there are four official modes
(defined in FIPS PUB 81). One is to go through the above-described
process for each block in succession. This is called Electronic Codebook
(ECB) mode. A stronger method is to exclusive-or each plaintext block
with the preceding ciphertext block prior to encryption. (The first
block is exclusive-or'ed with a secret 64-bit initialization vector
(IV).) This is called Cipher Block Chaining (CBC) mode. The other two
modes are Output Feedback (OFB) and Cipher Feedback (CFB).
;对超过64位的加密和解密,(美国)联邦信息处理标准 PUB 81 中定有四种方法。
;一种是连续的对每个数据块进行上述操作。这种方法被称 ECB mode。另一种更
;高强度的方法是在加密前,用前述的密文块对明文块进行异或操作。
# 括号里那句话不懂 :(
;这种方法被称为 CBC mode。还有两种方法是 OFB mode 和 CFB mode。
When it comes to padding the data block, there are several options. One
is to simply append zeros. Two suggested by FIPS PUB 81 are, if the data
is binary data, fill up the block with bits that are the opposite of the
last bit of data, or, if the data is ASCII data, fill up the block with
random bytes and put the ASCII character for the number of pad bytes in
the last byte of the block. Another technique is to pad the block with
random bytes and in the last 3 bits store the original number of data bytes.
;在填充数据块时(还记不记得,当数据块不足64位时要进行填充),有以下几种
;选择:一种就是填0。第二种是被(美国)联邦信息处理标准 PUB 81所建议的,如
;果数据是二进制的,就填入和数据位最后一位相反的数;如果数据块是ASCII码,
;就填入随机字节,并且将填充数目写入最后一个字节。另一种技术就是填入随机
;字节,并且将最后原数据字节数写入最后的三位。(注意:是位,bit)

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1371
1371
 52
52
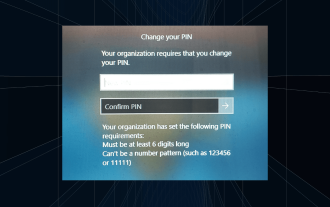 Lösung: Ihre Organisation verlangt von Ihnen, dass Sie Ihre PIN ändern
Oct 04, 2023 pm 05:45 PM
Lösung: Ihre Organisation verlangt von Ihnen, dass Sie Ihre PIN ändern
Oct 04, 2023 pm 05:45 PM
Auf dem Anmeldebildschirm wird die Meldung „Ihre Organisation hat Sie gebeten, Ihre PIN zu ändern“ angezeigt. Dies geschieht, wenn das PIN-Ablauflimit auf einem Computer erreicht wird, der organisationsbasierte Kontoeinstellungen verwendet und die Kontrolle über persönliche Geräte hat. Wenn Sie Windows jedoch über ein persönliches Konto einrichten, sollte die Fehlermeldung im Idealfall nicht erscheinen. Obwohl dies nicht immer der Fall ist. Die meisten Benutzer, die auf Fehler stoßen, melden dies über ihre persönlichen Konten. Warum fordert mich meine Organisation auf, meine PIN unter Windows 11 zu ändern? Es ist möglich, dass Ihr Konto mit einer Organisation verknüpft ist. Ihr primärer Ansatz sollte darin bestehen, dies zu überprüfen. Die Kontaktaufnahme mit Ihrem Domain-Administrator kann hilfreich sein! Darüber hinaus können falsch konfigurierte lokale Richtlinieneinstellungen oder falsche Registrierungsschlüssel Fehler verursachen. Im Augenblick
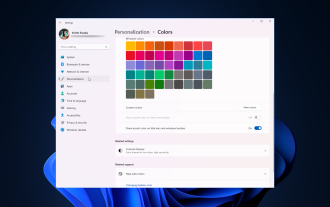 So passen Sie die Fensterrahmeneinstellungen unter Windows 11 an: Farbe und Größe ändern
Sep 22, 2023 am 11:37 AM
So passen Sie die Fensterrahmeneinstellungen unter Windows 11 an: Farbe und Größe ändern
Sep 22, 2023 am 11:37 AM
Windows 11 bringt frisches und elegantes Design in den Vordergrund; die moderne Benutzeroberfläche ermöglicht es Ihnen, feinste Details, wie zum Beispiel Fensterränder, zu personalisieren und zu ändern. In diesem Leitfaden besprechen wir Schritt-für-Schritt-Anleitungen, die Ihnen dabei helfen, eine Umgebung zu erstellen, die Ihrem Stil im Windows-Betriebssystem entspricht. Wie ändere ich die Fensterrahmeneinstellungen? Drücken Sie +, um die Einstellungen-App zu öffnen. WindowsIch gehe zu Personalisierung und klicke auf Farbeinstellungen. Farbänderung Fensterränder Einstellungen Fenster 11" Breite="643" Höhe="500" > Suchen Sie die Option Akzentfarbe auf Titelleiste und Fensterrändern anzeigen und schalten Sie den Schalter daneben um. Um Akzentfarben im Startmenü und in der Taskleiste anzuzeigen Um die Designfarbe im Startmenü und in der Taskleiste anzuzeigen, aktivieren Sie „Design im Startmenü und in der Taskleiste anzeigen“.
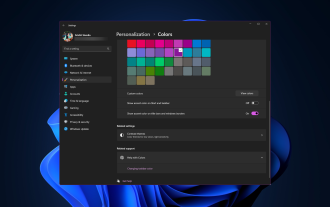 Wie ändere ich die Farbe der Titelleiste unter Windows 11?
Sep 14, 2023 pm 03:33 PM
Wie ändere ich die Farbe der Titelleiste unter Windows 11?
Sep 14, 2023 pm 03:33 PM
Standardmäßig hängt die Farbe der Titelleiste unter Windows 11 vom gewählten Dunkel-/Hell-Design ab. Sie können es jedoch in jede gewünschte Farbe ändern. In diesem Leitfaden besprechen wir Schritt-für-Schritt-Anleitungen für drei Möglichkeiten, wie Sie Ihr Desktop-Erlebnis ändern und personalisieren können, um es optisch ansprechend zu gestalten. Ist es möglich, die Farbe der Titelleiste von aktiven und inaktiven Fenstern zu ändern? Ja, Sie können die Farbe der Titelleiste aktiver Fenster mit der App „Einstellungen“ ändern, oder Sie können die Farbe der Titelleiste inaktiver Fenster mit dem Registrierungseditor ändern. Um diese Schritte zu lernen, fahren Sie mit dem nächsten Abschnitt fort. Wie ändere ich die Farbe der Titelleiste in Windows 11? 1. Drücken Sie in der App „Einstellungen“ +, um das Einstellungsfenster zu öffnen. WindowsIch gehe zu „Personalisierung“ und dann
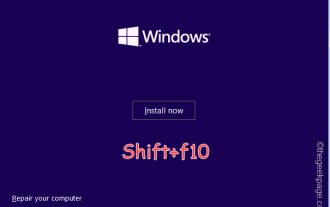 OOBELANGUAGE-Fehlerprobleme bei der Reparatur von Windows 11/10
Jul 16, 2023 pm 03:29 PM
OOBELANGUAGE-Fehlerprobleme bei der Reparatur von Windows 11/10
Jul 16, 2023 pm 03:29 PM
Wird auf der Windows Installer-Seite „Ein Problem ist aufgetreten“ zusammen mit der Anweisung „OOBELANGUAGE“ angezeigt? Aufgrund solcher Fehler bricht die Installation von Windows manchmal ab. OOBE bedeutet Out-of-the-Box-Erlebnis. Wie aus der Fehlermeldung hervorgeht, handelt es sich hierbei um ein Problem im Zusammenhang mit der OOBE-Sprachauswahl. Sie müssen sich keine Sorgen machen, Sie können dieses Problem durch eine geschickte Bearbeitung der Registrierung über den OOBE-Bildschirm selbst lösen. Schnelllösung – 1. Klicken Sie unten in der OOBE-App auf die Schaltfläche „Wiederholen“. Dadurch wird der Prozess ohne weitere Probleme fortgesetzt. 2. Verwenden Sie den Netzschalter, um das Herunterfahren des Systems zu erzwingen. Nach dem Neustart des Systems sollte OOBE fortgesetzt werden. 3. Trennen Sie das System vom Internet. Schließen Sie alle Aspekte von OOBE im Offline-Modus ab
 So aktivieren oder deaktivieren Sie die Vorschau von Miniaturansichten in der Taskleiste unter Windows 11
Sep 15, 2023 pm 03:57 PM
So aktivieren oder deaktivieren Sie die Vorschau von Miniaturansichten in der Taskleiste unter Windows 11
Sep 15, 2023 pm 03:57 PM
Miniaturansichten in der Taskleiste können Spaß machen, aber auch ablenken oder stören. Wenn man bedenkt, wie oft Sie mit der Maus über diesen Bereich fahren, haben Sie möglicherweise ein paar Mal versehentlich wichtige Fenster geschlossen. Ein weiterer Nachteil besteht darin, dass es mehr Systemressourcen verbraucht. Wenn Sie also nach einer Möglichkeit suchen, ressourceneffizienter zu arbeiten, zeigen wir Ihnen, wie Sie es deaktivieren können. Wenn Ihre Hardware-Spezifikationen jedoch dafür geeignet sind und Ihnen die Vorschau gefällt, können Sie sie aktivieren. Wie aktiviere ich die Miniaturvorschau der Taskleiste in Windows 11? 1. Tippen Sie in der App „Einstellungen“ auf die Taste und klicken Sie auf „Einstellungen“. Klicken Sie unter Windows auf „System“ und wählen Sie „Info“. Klicken Sie auf Erweiterte Systemeinstellungen. Navigieren Sie zur Registerkarte „Erweitert“ und wählen Sie unter „Leistung“ die Option „Einstellungen“ aus. Wählen Sie „Visuelle Effekte“
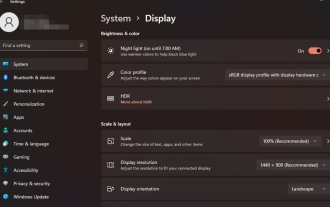 Anleitung zur Anzeigeskalierung unter Windows 11
Sep 19, 2023 pm 06:45 PM
Anleitung zur Anzeigeskalierung unter Windows 11
Sep 19, 2023 pm 06:45 PM
Wir alle haben unterschiedliche Vorlieben, wenn es um die Anzeigeskalierung unter Windows 11 geht. Manche Leute mögen große Symbole, andere mögen kleine Symbole. Wir sind uns jedoch alle einig, dass die richtige Skalierung wichtig ist. Eine schlechte Schriftartenskalierung oder eine Überskalierung von Bildern kann bei der Arbeit ein echter Produktivitätskiller sein. Sie müssen daher wissen, wie Sie sie anpassen können, um die Fähigkeiten Ihres Systems optimal zu nutzen. Vorteile des benutzerdefinierten Zooms: Dies ist eine nützliche Funktion für Personen, die Schwierigkeiten haben, Text auf dem Bildschirm zu lesen. Es hilft Ihnen, mehr gleichzeitig auf dem Bildschirm zu sehen. Sie können benutzerdefinierte Erweiterungsprofile erstellen, die nur für bestimmte Monitore und Anwendungen gelten. Kann dazu beitragen, die Leistung von Low-End-Hardware zu verbessern. Dadurch haben Sie mehr Kontrolle darüber, was auf Ihrem Bildschirm angezeigt wird. So verwenden Sie Windows 11
 10 Möglichkeiten, die Helligkeit unter Windows 11 anzupassen
Dec 18, 2023 pm 02:21 PM
10 Möglichkeiten, die Helligkeit unter Windows 11 anzupassen
Dec 18, 2023 pm 02:21 PM
Die Bildschirmhelligkeit ist ein wesentlicher Bestandteil der Nutzung moderner Computergeräte, insbesondere wenn Sie über einen längeren Zeitraum auf den Bildschirm schauen. Es hilft Ihnen, die Belastung Ihrer Augen zu reduzieren, die Lesbarkeit zu verbessern und Inhalte einfach und effizient anzuzeigen. Abhängig von Ihren Einstellungen kann es jedoch manchmal schwierig sein, die Helligkeit zu verwalten, insbesondere unter Windows 11 mit den neuen Änderungen an der Benutzeroberfläche. Wenn Sie Probleme beim Anpassen der Helligkeit haben, finden Sie hier alle Möglichkeiten, die Helligkeit unter Windows 11 zu verwalten. So ändern Sie die Helligkeit unter Windows 11 [10 Möglichkeiten erklärt] Benutzer eines einzelnen Monitors können die folgenden Methoden verwenden, um die Helligkeit unter Windows 11 anzupassen. Hierzu zählen sowohl Desktop-Systeme mit einem einzelnen Monitor als auch Laptops. Lasst uns beginnen. Methode 1: Verwenden Sie das Action Center. Das Action Center ist zugänglich
 So beheben Sie den Aktivierungsfehlercode 0xc004f069 in Windows Server
Jul 22, 2023 am 09:49 AM
So beheben Sie den Aktivierungsfehlercode 0xc004f069 in Windows Server
Jul 22, 2023 am 09:49 AM
Der Aktivierungsprozess unter Windows nimmt manchmal eine plötzliche Wendung und zeigt eine Fehlermeldung mit diesem Fehlercode 0xc004f069 an. Obwohl der Aktivierungsprozess online erfolgt, kann dieses Problem bei einigen älteren Systemen mit Windows Server auftreten. Führen Sie diese ersten Prüfungen durch. Wenn sie Ihnen bei der Aktivierung Ihres Systems nicht weiterhelfen, fahren Sie mit der Hauptlösung fort, um das Problem zu beheben. Problemumgehung – Schließen Sie die Fehlermeldung und das Aktivierungsfenster. Starten Sie dann Ihren Computer neu. Wiederholen Sie den Windows-Aktivierungsprozess noch einmal von Grund auf. Fix 1 – Aktivierung über das Terminal. Aktivieren Sie das Windows Server Edition-System über das CMD-Terminal. Stufe – 1 Überprüfen Sie die Windows Server-Version. Sie müssen überprüfen, welchen W-Typ Sie verwenden




