Maximale Teilsequenz- und Algorithmusanalyse
Problembeschreibung: Gegeben n ganzzahlige Folgen {a1, a2,...,an}, finden Sie die Funktion f(i,j)=max{0,Σak} (k: stetig von i bis j);
Das Problem besteht darin, den Maximalwert der Summe aufeinanderfolgender Unterspalten zu finden. Wenn der Maximalwert eine negative Zahl ist, nehmen Sie 0, z. B. die 8er-Zahlenfolge {-1, 2, -3 ,4,-2,5,-8,3}, die maximale Teilsequenzsumme von Namo beträgt 4 (-2) 5=7.
Dieses Problem hat vier Algorithmus mit unterschiedlicher Komplexität, die zeitliche Komplexität der Algorithmen 1 bis 4 beträgt O(n3), O(n2), O(nlogn), O(n);
Algorithmus 1:
Die direkteste Methode ist die erschöpfende Methode. Wir können das linke Ende i und das rechte Ende j der Teilsequenz festlegen und dann eine Ebene verwenden, um a[i ] zur Summe von a[j].
//Maximale Unterspalte und erschöpfende Methode
#include
using namespace std;
int Find_Maxsun(int*a, int n ) ;
int main(){
int n, i;
int a[100];
cin >> n;
cout << << n << "Nummer:" << endl;
für (i = 0; i < n; i )
cout<
}
int Find_Maxsun(int*a, int n){
int MaxSun = 0, i , j, k;
int NowSum;
for (i = 0; i < n; i ) /*linkes Ende der Teilsequenz*/
for (j = 0; j < n; j ){ /*Rechtes Ende der Teilsequenz*/
NowSum = 0;
for (k = i; k <= j; k )
NowSum = a[k]; /*From a[i ] zu einer Teilfolge von [j]*/
if (NowSum>MaxSun)
MaxSun = NowSum; /*Update result*/
}
return MaxSun;
}
3). Dies ist natürlich der dümmste Algorithmus, aber wenn die Daten sehr groß sind, selbst wenn es so ist ist toter Rhythmus, wir können die dritte Ebene der for-Schleife deutlich erkennen. Jedes Mal, wenn
j hinzugefügt wird, muss die Unterspaltensumme erneut berechnet werden. Warum verwenden wir also nicht das Ergebnis von j? 1? Das heißt, wir speichern das Ergebnis von j-1. Bei der Berechnung des Ergebnisses von Schritt j müssen wir nur a[j] auf der Grundlage von Schritt j-1 hinzufügen, sodass es Algorithmus 2 gibt. Algorithmus 2: #includeusing namespace std;
int Find_Maxsun2(int*a, int n);
int main(){
int n, i;
int a[100];
cin >> n;
cout << :" << endl;
for (i = 0; i < n; i )
cin >> a[i];
cout << Find_Maxsun2(a, n ) << endl;
return 0;
}
int Find_Maxsun2(int*a, int n){
int i, j, NewSum = 0, MaxSum= 0;
for (i = 0; i < n; i ){ /*ist der linke Endpunkt der Sequenz*/
NewSum = 0;
for (j = i; j < n; j ){ / *j Für den rechten Endpunkt der Reihe*/
NewSum = a[j]; /*Update NewSum jedes Mal unter j-1-Bedingung*/
if (NewSum>MaxSum) /*Update MaxSum*/
MaxSum = NewSum;
}
}
return MaxSum;
}
2), was offensichtlich besser ist. Nicht die Komplexität, die wir wollen.
Algorithmus 3: Algorithmus 3 nutzt die Idee des Teilens und Herrschens. Die Grundidee ist selbstverständlich: Erst teilen und dann erobern, das Problem in kleine Probleme zerlegen und Um die kleinen Probleme zu lösen, teilen wir die ursprüngliche Sequenz in zwei Teile, dann befindet sich die größte Teilsequenz links, rechts oder jenseits der Grenze. Die Grundidee ist wie folgt: Schritt 1: Teilen Sie die ursprüngliche Sequenz in zwei Teile und teilen Sie sie in eine linke Sequenz und eine rechte Sequenz auf. Schritt 2: Finden Sie rekursiv die Teilfolgen S left und S right. Teil 3: Scannen Sie von der Mittellinie nach beiden Seiten, um die größte Teilfolge über die Mittellinie und S zu finden. Schritt 4: Finden Sie S=max{S links, S Mitte, S rechts} Der Code wird wie folgt implementiert:#include
using namespace std;
int Find_MaxSum3(int*a,int low,int high);
int Max(int a,int b,int c);
int main(){
int n, i;
int a[100];
cin >>
cout << < n << " Zahl:" << für (i = 0; i < n; i )
cout < < Find_MaxSum3(a,0,n-1) << endl;
return 0;
}
int Find_MaxSum3(int*a,int low,int high){
int MaxSum = 0, MidSum, LeftSum, RightSum,i;
MidSum = 0;
if (low == high){ /*Abbruchbedingung der Rekursion*/
if (a[low] > 0)
return a[low];
else
return 0;
}
int mid = (low high) / 2; //Finde den Mittelpunkt der Punktzahl
LeftSum = Find_MaxSum3(a, low, mid); /*Rekursiv die maximale Summe der linken Sequenz ermitteln*/
RightSum = Find_MaxSum3(a, mid 1, high); /*Rekursiv die maximale Teilsequenzsumme der rechten Sequenz ermitteln */
/*Dann können Sie die maximale Summe der grenzüberschreitenden Zwischensequenzen ermitteln */
int NewLeft = 0,Max_BorderLeft=0, NewRight = 0,Max_BorderRight=0;
für (i = mid; i >= low; i--) { /*Nach links scannen, um die maximale Summe zu finden*/
NewLeft = a[i];
if (NewLeft > Max_BorderLeft)
Max_BorderLeft = NewLeft ;
}
for (i = mid 1; i <= high; i ){ /*Nach rechts scannen, um die größte Teilsequenz zu finden und*/
NewRight =a[i];
if (NewRight >= Max_BorderRight)
Max_BorderRight = NewRight ;
}
MidSum = Max_BorderRight Max_BorderLeft;
return Max(LeftSum, MidSum, RightSum); /*Gibt das Ergebnis der Behandlung zurück*/
}
int Max(int a, int b, int c){ /*Finde die größte Zahl unter den 3*/
if ( a>= b&&a >= c)
return a ;
if (b >= a&&b >= c )
return b;
if (c >= b&&c>=a)
return c;
}
Berechnen wir die zeitliche Komplexität dieses Algorithmus:
T(1)=1;
T(n)=2T(n/2) O(n);
=2
kT( n/2k) kO(n)=2kT(1) kO(n) (wobei n=2 k)=n nlogn=O (nlogn);Obwohl dieser Algorithmus sehr gut ist, ist er nicht der schnellste.
Algorithmus 4:
Algorithmus 4 wird Online-Verarbeitung genannt. Dies bedeutet, dass jedes Mal, wenn ein Datenelement eingelesen wird, es rechtzeitig verarbeitet wird und das erhaltene Ergebnis für die aktuell gelesenen Daten gilt, dh der Algorithmus kann an jeder Position die richtige Lösung liefern und der Algorithmus kann geben beim Lesen die richtige Lösung finden.
#include
int Find_MaxSum4(int*a, int n);
int main(){
int n, i;
int a[100];
cin >> cout << 🎜> for (i = 0; i < n; i )
cin >> a[i];
cout << Find_MaxSum4(a,n) << > return 0;
}
int Find_MaxSum4(int*a, int n){
int i, NewSum = 0, MaxSum = 0;
for (i = 0; i < n; i ){
NewSum = a[i]; /*Aktuelle Teilsequenzsumme*/
if (MaxSum < NewSum)
MaxSum = NewSum; /*Maximale Teilsequenzsumme aktualisieren*/
if ( NewSum < 0) /*Wenn es kleiner als 0 ist, verwerfen Sie es*/
NewSum = 0;
}
return MaxSum;
}
Dieser Algorithmus liest The Die Daten werden einzeln gescannt und es gibt nur eine for-Schleife. Die Algorithmen zur Lösung desselben Problems sind sehr unterschiedlich. Der Trick besteht darin, den Computer einige wichtige Zwischenergebnisse merken zu lassen, um wiederholte Berechnungen zu vermeiden.
Das Obige stellt die maximale Teilsequenz- und Algorithmusanalyse vor, einschließlich Aspekten des Inhalts. Ich hoffe, dass es für Freunde hilfreich ist, die sich für PHP-Tutorials interessieren.

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1393
1393
 52
52
 1209
1209
 24
24
 Was sind die Unterschiede zwischen Huawei GT3 Pro und GT4?
Dec 29, 2023 pm 02:27 PM
Was sind die Unterschiede zwischen Huawei GT3 Pro und GT4?
Dec 29, 2023 pm 02:27 PM
Viele Benutzer werden sich bei der Auswahl von Smartwatches für die Marke Huawei entscheiden. Viele Benutzer sind neugierig auf den Unterschied zwischen Huawei GT3pro und GT4. Was sind die Unterschiede zwischen Huawei GT3pro und GT4? 1. Aussehen GT4: 46 mm und 41 mm, das Material ist Glasspiegel + Edelstahlgehäuse + hochauflösende Faserrückschale. GT3pro: 46,6 mm und 42,9 mm, das Material ist Saphirglas + Titangehäuse/Keramikgehäuse + Keramikrückschale 2. Gesundes GT4: Mit dem neuesten Huawei Truseen5.5+-Algorithmus werden die Ergebnisse genauer. GT3pro: EKG-Elektrokardiogramm sowie Blutgefäß und Sicherheit hinzugefügt
 Detaillierte Erläuterung der Verwendung von Return in der C-Sprache
Oct 07, 2023 am 10:58 AM
Detaillierte Erläuterung der Verwendung von Return in der C-Sprache
Oct 07, 2023 am 10:58 AM
Die Verwendung von return in der C-Sprache ist: 1. Für Funktionen, deren Rückgabewerttyp ungültig ist, können Sie die Rückgabeanweisung verwenden, um die Ausführung der Funktion vorzeitig zu beenden. 2. Für Funktionen, deren Rückgabewerttyp nicht ungültig ist, ist die Funktion von Die Return-Anweisung dient dazu, die Ausführung der Funktion zu beenden. 3. Beenden Sie die Ausführung der Funktion vorzeitig wenn die Funktion keinen Wert zurückgibt.
 Detaillierte Erläuterung der Methode zum Konvertieren des Int-Typs in Bytes in PHP
Mar 06, 2024 pm 06:18 PM
Detaillierte Erläuterung der Methode zum Konvertieren des Int-Typs in Bytes in PHP
Mar 06, 2024 pm 06:18 PM
Ausführliche Erläuterung der Methode zum Konvertieren des Int-Typs in Byte in PHP. In PHP müssen wir häufig den Integer-Typ (int) in den Byte-Typ (Byte) konvertieren, beispielsweise wenn es um Netzwerkdatenübertragung, Dateiverarbeitung oder Verschlüsselungsalgorithmen geht . In diesem Artikel wird detailliert beschrieben, wie der Typ int in den Typ byte konvertiert wird, und es werden spezifische Codebeispiele bereitgestellt. 1. Die Beziehung zwischen int-Typ und Byte Im Computerbereich stellt der grundlegende Datentyp int eine Ganzzahl dar, während Byte (Byte) eine Computerspeichereinheit ist, normalerweise 8-Bit-Binärdaten
 Wie ist die Ausführungsreihenfolge von Return- und Final-Anweisungen in Java?
Apr 25, 2023 pm 07:55 PM
Wie ist die Ausführungsreihenfolge von Return- und Final-Anweisungen in Java?
Apr 25, 2023 pm 07:55 PM
Quellcode: publicclassReturnFinallyDemo{publicstaticvoidmain(String[]args){System.out.println(case1());}publicstaticintcase1(){intx;try{x=1;returnx;}finally{x=3;}}}# Ausgabe Die Ausgabe des obigen Codes kann einfach zu dem Schluss kommen: return wird ausgeführt, bevor wir uns schließlich ansehen, was auf der Bytecode-Ebene passiert. Im Folgenden wird ein Teil des Bytecodes der Methode case1 abgefangen und mit dem Quellcode verglichen, um die Bedeutung jeder Anweisung darin zu kommentieren
 Fix: Snipping-Tool funktioniert unter Windows 11 nicht
Aug 24, 2023 am 09:48 AM
Fix: Snipping-Tool funktioniert unter Windows 11 nicht
Aug 24, 2023 am 09:48 AM
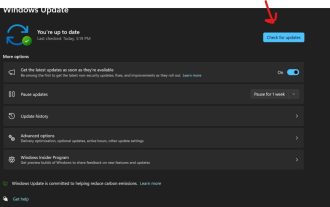
Warum das Snipping-Tool unter Windows 11 nicht funktioniert Das Verständnis der Grundursache des Problems kann dabei helfen, die richtige Lösung zu finden. Hier sind die häufigsten Gründe, warum das Snipping Tool möglicherweise nicht ordnungsgemäß funktioniert: Focus Assistant ist aktiviert: Dies verhindert, dass das Snipping Tool geöffnet wird. Beschädigte Anwendung: Wenn das Snipping-Tool beim Start abstürzt, ist es möglicherweise beschädigt. Veraltete Grafiktreiber: Inkompatible Treiber können das Snipping-Tool beeinträchtigen. Störungen durch andere Anwendungen: Andere laufende Anwendungen können mit dem Snipping Tool in Konflikt geraten. Das Zertifikat ist abgelaufen: Ein Fehler während des Upgrade-Vorgangs kann zu diesem Problem führen. Diese einfache Lösung ist für die meisten Benutzer geeignet und erfordert keine besonderen technischen Kenntnisse. 1. Aktualisieren Sie Windows- und Microsoft Store-Apps
 C++-Programm zum Konvertieren von Variablen vom Typ Double in den Typ int
Aug 25, 2023 pm 08:25 PM
C++-Programm zum Konvertieren von Variablen vom Typ Double in den Typ int
Aug 25, 2023 pm 08:25 PM
In C++ können Variablen vom Typ int nur positive oder negative Ganzzahlwerte enthalten; sie können keine Dezimalwerte enthalten. Hierfür stehen Float- und Double-Werte zur Verfügung. Der Datentyp double wurde erstellt, um Dezimalzahlen mit bis zu sieben Nachkommastellen zu speichern. Die Konvertierung einer Ganzzahl in einen Double-Datentyp kann automatisch vom Compiler durchgeführt werden (sogenannte „implizite“ Konvertierung) oder sie kann vom Programmierer explizit vom Compiler angefordert werden (sogenannte „explizite“ Konvertierung). In den folgenden Abschnitten werden wir verschiedene Konvertierungsmethoden behandeln. Implizite Konvertierungen Der Compiler führt implizite Typkonvertierungen automatisch durch. Um dies zu erreichen, sind zwei Variablen erforderlich – eine vom Typ Gleitkomma und die andere vom Typ Ganzzahl. Wenn wir einer Ganzzahlvariablen einfach einen Gleitkommawert oder eine Variable zuweisen, kümmert sich der Compiler um alle anderen Dinge
 Was ist der Wertebereich von int32?
Aug 11, 2023 pm 02:53 PM
Was ist der Wertebereich von int32?
Aug 11, 2023 pm 02:53 PM
Der Wertebereich von int32 reicht von -2 bis 31. Potenz bis 2 bis 31. Potenz minus 1, also -2147483648 bis 2147483647. int32 ist ein vorzeichenbehafteter Ganzzahltyp, was bedeutet, dass er positive Zahlen, negative Zahlen und Nullen darstellen kann. Er verwendet 1 Bit zur Darstellung des Vorzeichenbits und die restlichen 31 Bits werden zur Darstellung des numerischen Werts verwendet. Da ein Bit zur Darstellung des Vorzeichenbits verwendet wird, beträgt die effektive Anzahl der int32-Bits 31.
 So konvertieren Sie int in den String-Typ in der Go-Sprache
Jun 04, 2021 pm 03:56 PM
So konvertieren Sie int in den String-Typ in der Go-Sprache
Jun 04, 2021 pm 03:56 PM
Konvertierungsmethode: 1. Verwenden Sie die Funktion Itoa(), die Syntax „strconv.Itoa(num)“ 2. Verwenden Sie die Funktion FormatInt(), um Daten vom Typ int in die angegebene Basis zu konvertieren und sie in Form einer Zeichenfolge zurückzugeben. die Syntax „strconv .FormatInt(num,10)“.




