Berechnen Sie den Wert von π mit Python
π ist eine wahrhaft magische Zahl, der unzählige Menschen folgen. Ich bin mir nicht ganz sicher, was das Faszinierende an einer irrationalen Zahl ist, die sich ewig wiederholt. Meiner Meinung nach macht es mir Spaß, π zu berechnen, also den Wert von π zu berechnen. Da π eine irrationale Zahl ist, ist sie unendlich. Dies bedeutet, dass jede Berechnung von π nur eine Näherung ist. Wenn Sie 100 Ziffern berechnen, kann ich 101 Ziffern berechnen und bin präziser. Bisher haben einige Supercomputer ausgewählt, um zu versuchen, das genaueste π zu berechnen. Einige Extremwerte umfassen die Berechnung von 500 Millionen Stellen von Pi. Sie können online sogar eine Textdatei finden, die 10 Milliarden Ziffern von π enthält (seien Sie vorsichtig! Das Herunterladen dieser Datei kann eine Weile dauern und sie lässt sich nicht mit Ihrer üblichen Notepad-Anwendung öffnen.). Für mich interessiert es, wie man π mit ein paar Zeilen einfachem Python berechnet.

Sie können jederzeit die Variable math.pi verwenden. Es ist in der Standardbibliothek enthalten und Sie sollten es verwenden, bevor Sie versuchen, es selbst zu berechnen. Tatsächlich werden wir es zur Berechnung der Genauigkeit verwenden. Schauen wir uns zunächst eine sehr einfache Methode zur Berechnung von Pi an. Wie üblich verwende ich Python 2.7, die gleichen Ideen und der gleiche Code gelten möglicherweise für verschiedene Versionen. Die meisten der von uns verwendeten Algorithmen stammen von der Pi-Wikipedia-Seite und sind dort implementiert. Schauen wir uns den folgenden Code an:
importsys
importmath
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=1.0
b=1.0/math.sqrt(2)
t=1.0/4.0
p=1.0
foriinrange(int(sys.argv[1])):
at=(a+b)/2
bt=math.sqrt(a*b)
tt=t-p*(a-at)**2
pt=2*p
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(math.pi-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
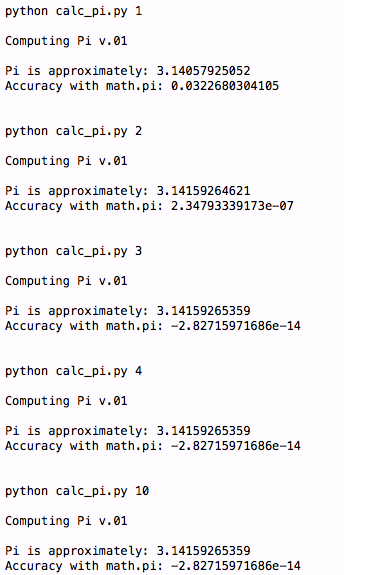
main(sys.argv[1:])Dies ist ein sehr einfaches Skript, das Sie nach Belieben herunterladen, ausführen, ändern und mit anderen teilen können. Sie können eine Ausgabe ähnlich der folgenden sehen:

Sie werden feststellen, dass wir es sind, auch wenn n größer als 4 ist Annäherung an die Pi-Genauigkeit, aber keine große Verbesserung. Wir können vermuten, dass selbst wenn der Wert von n größer ist, das Gleiche (die Näherungsgenauigkeit von Pi wird nicht verbessert) immer noch passieren wird. Glücklicherweise gibt es mehr als einen Weg, dieses Rätsel zu lösen. Mit der Python Decimal (Dezimal)-Bibliothek können wir Werte mit höherer Genauigkeit erhalten, um Pi anzunähern. Sehen wir uns an, wie die Bibliotheksfunktionen verwendet werden. Diese vereinfachte Version kann Zahlen mit mehr als 11 Ziffern erhalten, die normalerweise weniger genau sind als Python-Gleitkommazahlen. Hier ist ein Beispiel aus der Python Decimal-Bibliothek:

Sehen Sie sich diese Zahlen an. falsch! Wir haben nur 3.14 eingegeben, warum haben wir etwas Müll bekommen? Das ist Speichermüll. Kurz gesagt: Python liefert Ihnen die gewünschte Dezimalzahl plus einen kleinen zusätzlichen Wert. Es hat keinen Einfluss auf Berechnungen, solange die Genauigkeit zu Beginn geringer ist als die vorherige Junk-Zahl. Sie können angeben, wie viele Ziffern Sie möchten, indem Sie getcontext().prec festlegen. Versuchen wir es.
Sehr gut. Versuchen wir nun, dies zu nutzen, um zu sehen, ob wir eine bessere Annäherung an unseren vorherigen Code erreichen können. Normalerweise bin ich gegen die Verwendung von „ from Library Import * “, aber in diesem Fall sieht der Code dadurch hübscher aus.
importsys
importmath
fromdecimalimport*
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=Decimal(1.0)
b=Decimal(1.0/math.sqrt(2))
t=Decimal(1.0)/Decimal(4.0)
p=Decimal(1.0)
foriinrange(int(sys.argv[1])):
at=Decimal((a+b)/2)
bt=Decimal(math.sqrt(a*b))
tt=Decimal(t-p*(a-at)**2)
pt=Decimal(2*p)
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])Ausgabeergebnis:
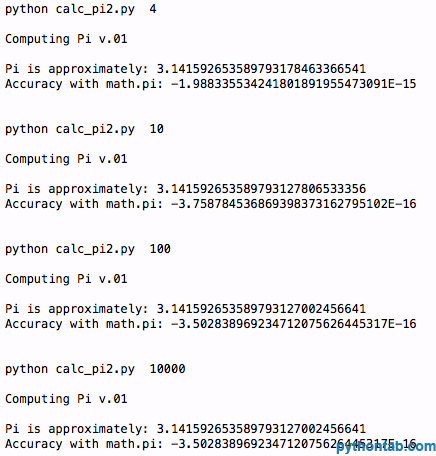
Okay. Wir sind genauer, aber es sieht so aus, als ob es eine gewisse Rundung gibt. Ab n = 100 und n = 1000 haben wir die gleiche Genauigkeit. Was nun? Okay, jetzt wenden wir uns den Formeln zu. Bisher haben wir Pi berechnet, indem wir seine Teile addieren. Ich habe Code aus DANs Artikel zur Berechnung von Pi gefunden. Er schlug vor, dass wir die folgenden drei Formeln verwenden:
Bailey-Borwein-Plouffe-Formel
Bellard-Formel
Chudnovsky-Algorithmus
Beginnen wir mit Bailey– Die Borwein-Plouffe-Formel beginnt. Es sieht so aus:
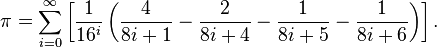
Im Code können wir es so schreiben:
import sys
import math
from decimal import *
def bbp(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k+=1
return pi
def main(argv):
if len(argv) !=2:
sys.exit('Usage: BaileyBorweinPlouffe.py <prec> <n>')
getcontext().prec=(int(sys.argv[1]))
my_pi=bbp(int(sys.argv[2]))
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if __name__=="__main__":
main(sys.argv[1:])Ohne den „Wrapper“-Code BBP (N) Funktion ist das, was Sie wirklich wollen. Je größer N Sie angeben und je größer der Wert, den Sie für getcontext().prec festlegen, desto präziser wird die Berechnung. Schauen wir uns einige Codeergebnisse an:
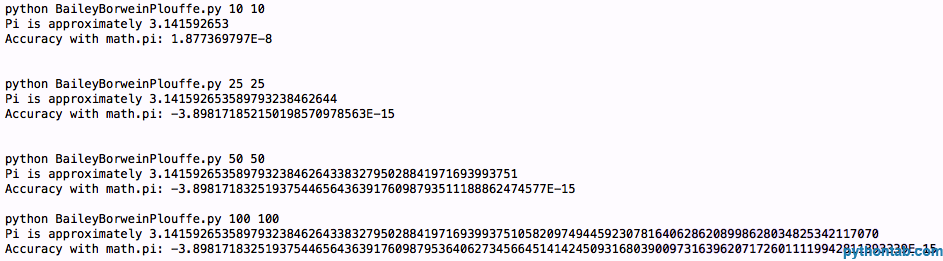
Das sind viele Ziffern. Sie sehen, dass wir nicht genauer sind als zuvor. Wir müssen also zur nächsten Formel, Bellahs Formel, übergehen und hoffentlich eine bessere Genauigkeit erreichen. Es wird so aussehen:
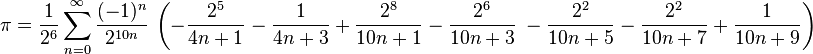
Wir werden nur unsere Transformationsformel ändern, der Rest des Codes bleibt gleich. Klicken Sie hier, um Bellas in Python implementierte Formel herunterzuladen. Werfen wir einen Blick auf bellards(n):
def bellard(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1)+Decimal(1)/(10*k+9)-Decimal(64)/(10*k+3)-Decimal(32)/(4*k+1)-Decimal(4)/(10*k+5)-Decimal(4)/(10*k+7)-Decimal(1)/(4*k+3))
k+=1
pi=pi*1/(2**6)
return piAusgabe:
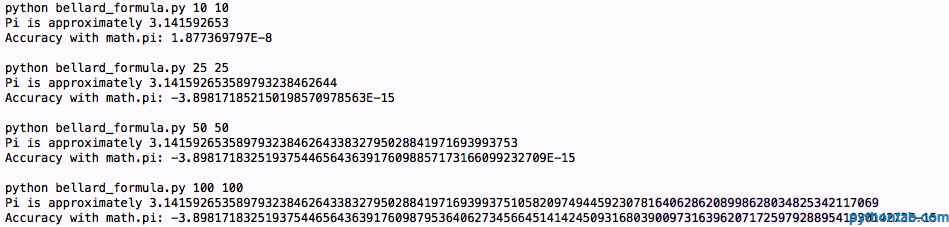
哦,不,我们得到的是同样的精度。好吧,让我们试试第三个公式, Chudnovsky 算法,它看起来是这个样子:
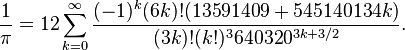
再一次,让我们看一下这个计算公式(假设我们有一个阶乘公式)。 点击这里可下载用 python 实现的 Chudnovsky 公式。
下面是程序和输出结果:
def chudnovsky(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))*(13591409+545140134*k)/(640320**(3*k)))
k+=1
pi=pi*Decimal(10005).sqrt()/4270934400
pi=pi**(-1)
return pi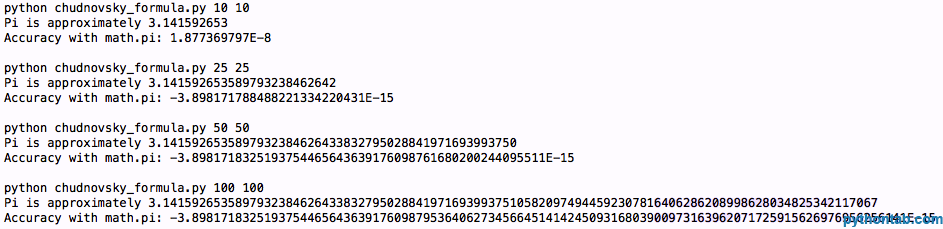
所以我们有了什么结论?花哨的算法不会使机器浮点世界达到更高标准。我真的很期待能有一个比我们用求和公式时所能得到的更好的精度。我猜那是过分的要求。如果你真的需要用PI,就只需使用math.pi变量了。然而,作为乐趣和测试你的计算机真的能有多快,你总是可以尝试第一个计算出Pi的百万位或者更多位是几。

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Wie löste ich das Problem der Berechtigungen beim Betrachten der Python -Version in Linux Terminal?
Apr 01, 2025 pm 05:09 PM
Wie löste ich das Problem der Berechtigungen beim Betrachten der Python -Version in Linux Terminal?
Apr 01, 2025 pm 05:09 PM
Lösung für Erlaubnisprobleme beim Betrachten der Python -Version in Linux Terminal Wenn Sie versuchen, die Python -Version in Linux Terminal anzuzeigen, geben Sie Python ein ...
 Wie kann ich die gesamte Spalte eines Datenrahmens effizient in einen anderen Datenrahmen mit verschiedenen Strukturen in Python kopieren?
Apr 01, 2025 pm 11:15 PM
Wie kann ich die gesamte Spalte eines Datenrahmens effizient in einen anderen Datenrahmen mit verschiedenen Strukturen in Python kopieren?
Apr 01, 2025 pm 11:15 PM
Bei der Verwendung von Pythons Pandas -Bibliothek ist das Kopieren von ganzen Spalten zwischen zwei Datenrahmen mit unterschiedlichen Strukturen ein häufiges Problem. Angenommen, wir haben zwei Daten ...
 Was sind einige beliebte Python -Bibliotheken und ihre Verwendung?
Mar 21, 2025 pm 06:46 PM
Was sind einige beliebte Python -Bibliotheken und ihre Verwendung?
Mar 21, 2025 pm 06:46 PM
In dem Artikel werden beliebte Python-Bibliotheken wie Numpy, Pandas, Matplotlib, Scikit-Learn, TensorFlow, Django, Flask und Anfragen erörtert, die ihre Verwendung in wissenschaftlichen Computing, Datenanalyse, Visualisierung, maschinellem Lernen, Webentwicklung und h beschreiben
 Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen ohne Serving_forver () an?
Apr 01, 2025 pm 10:51 PM
Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen ohne Serving_forver () an?
Apr 01, 2025 pm 10:51 PM
Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen an? Uvicorn ist ein leichter Webserver, der auf ASGI basiert. Eine seiner Kernfunktionen ist es, auf HTTP -Anfragen zu hören und weiterzumachen ...
 Wie erstelle ich dynamisch ein Objekt über eine Zeichenfolge und rufe seine Methoden in Python auf?
Apr 01, 2025 pm 11:18 PM
Wie erstelle ich dynamisch ein Objekt über eine Zeichenfolge und rufe seine Methoden in Python auf?
Apr 01, 2025 pm 11:18 PM
Wie erstellt in Python ein Objekt dynamisch über eine Zeichenfolge und ruft seine Methoden auf? Dies ist eine häufige Programmieranforderung, insbesondere wenn sie konfiguriert oder ausgeführt werden muss ...
 Wie behandle ich die mit Kommas getrennten Listen-Abfrageparameter in Fastapi?
Apr 02, 2025 am 06:51 AM
Wie behandle ich die mit Kommas getrennten Listen-Abfrageparameter in Fastapi?
Apr 02, 2025 am 06:51 AM
Fastapi ...
 Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer-Anfänger-Programmierbasis in Projekt- und problemorientierten Methoden?
Apr 02, 2025 am 07:18 AM
Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer-Anfänger-Programmierbasis in Projekt- und problemorientierten Methoden?
Apr 02, 2025 am 07:18 AM
Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer -Anfänger für Programmierungen? Wenn Sie nur 10 Stunden Zeit haben, um Computer -Anfänger zu unterrichten, was Sie mit Programmierkenntnissen unterrichten möchten, was würden Sie dann beibringen ...
 Was sind reguläre Ausdrücke?
Mar 20, 2025 pm 06:25 PM
Was sind reguläre Ausdrücke?
Mar 20, 2025 pm 06:25 PM
Regelmäßige Ausdrücke sind leistungsstarke Tools für Musteranpassung und Textmanipulation in der Programmierung, wodurch die Effizienz bei der Textverarbeitung in verschiedenen Anwendungen verbessert wird.