Verschiedene Sortieralgorithmen und Implementierungen in Java

Werfen wir zunächst einen Blick auf die Beziehung zwischen den 8 Sortierarten:

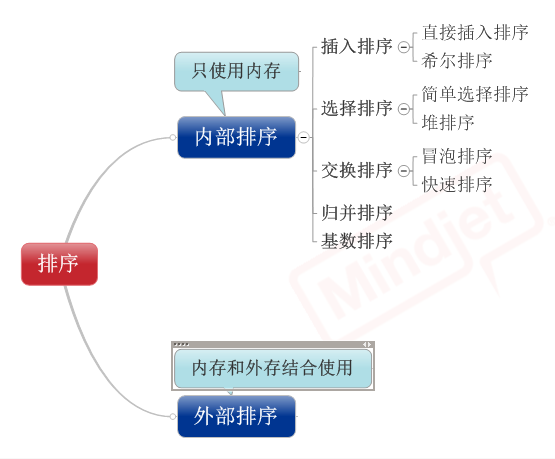
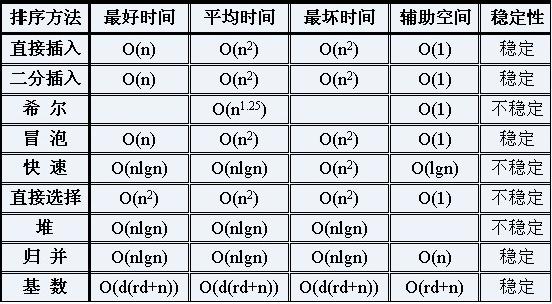
Die folgende Abbildung ist ein Vergleich verschiedener Sortierungen:

1, Direkteinfügungssortierung

(1) Grundidee: In Die zu sortierende Spalte In der Gruppennummer müssen wir nun unter der Annahme, dass die vorherigen (n-1) [n>=2] Zahlen bereits in

Reihenfolge sind, die n-te Zahl in die zuvor geordnete Zahl einfügen , sodass n Die Zahlen

auch der Reihe nach angeordnet sind. Wiederholen Sie diesen Zyklus, bis alles in Ordnung ist.

Wenn im Einfügealgorithmus eine Mindestzahl am Ende des Arrays vorhanden ist, bewegt sich der Einfügealgorithmus von der letzten

Position zur ersten.

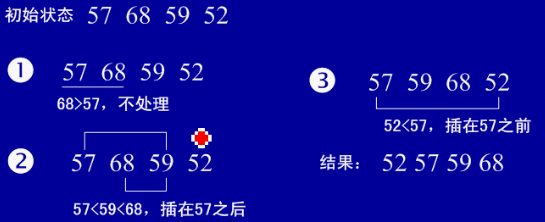
(2) Beispiel

package cglib;

 

public class StringNumber {
    
      public static void insertSort(int[] a) {  
            if (a == null || a.length < 2) {  
                return;  
            }  
            int length=a.length; //数组长度  
            int j;               //当前值的位置  
            int i;               //指向j前的位置  
            int key;             //当前要进行插入排序的值  
            //从数组的第二个位置开始遍历值  
            for(j=1;j<length;j++){  
                key=a[j];  
                i=j-1;
                System.out.println(" 将i="+i);
                //a[i]比当前值大时，a[i]后移一位,空出i的位置，好让下一次循环的值后移  
                while(i>=0 && a[i]>key){
                    System.out.println("进 i="+i);
                    a[i+1]=a[i]; //将a[i]值后移  
                    i--;         //i前移  
                    System.out.println(" i="+i);
                }//跳出循环(找到要插入的中间位置或已遍历到0下标)
                System.out.println(" 退出while");
                System.out.println(" i="+i);
                a[i+1]=key;    //将当前值插入  
            }  
        }  
        
      
        public static void main(String[] args) {  
            int[] array = { 3, -1, 0, -8, 2, 1 };  
            ArrayUtils.printArray(array);  
            insertSort(array);  
            ArrayUtils.printArray(array);  
        }
}

class ArrayUtils {  
    
    public static void printArray(int[] array) {  
        System.out.print("{");  
        for (int i = 0; i < array.length; i++) {  
            System.out.print(array[i]);  
            if (i < array.length - 1) {  
                System.out.print(", ");  
            }  
        }  
        System.out.println("}");  
    }  
}

Ausgabe:

{3, -1, 0, -8, 2, 1}
 将i=0
进 i=0
 i=-1
 退出while
 i=-1
 将i=1
进 i=1
 i=0
 退出while
 i=0
 将i=2
进 i=2
 i=1
进 i=1
 i=0
进 i=0
 i=-1
 退出while
 i=-1
 将i=3
进 i=3
 i=2
 退出while
 i=2
 将i=4
进 i=4
 i=3
进 i=3
 i=2
 退出while
 i=2
{-8, -1, 0, 1, 2, 3}

Hill-Sortierung (Sortierung mit minimalem Inkrement)

Grundalgorithmus:

Teilen Sie zunächst die gesamte Sequenz der zu sortierenden Elemente in mehrere Teilsequenzen (getrennt durch ein bestimmtes „Inkrement“). (bestehend aus „Anzahl“ von Elementen) werden direkt eingefügt bzw. sortiert, und dann werden die Inkremente sukzessive reduziert und dann sortiert. Wenn die Elemente in der gesamten Sequenz im Wesentlichen in der richtigen Reihenfolge sind (das Inkrement ist klein genug), erfolgt eine direkte Einfügungssortierung wird an allen Elementen durchgeführt. Da die direkte Einfügungssortierung sehr effizient ist, wenn die Elemente grundsätzlich geordnet sind (nahe dem besten Fall), ist die Hill-Sortierung zeiteffizienter als die ersten beiden Methoden. Die Wahl der Schrittgröße ist ein wichtiger Teil der Hill-Sortierung. Jede Schrittfolge funktioniert, solange der letzte Schritt 1 ist.

Der Algorithmus sortiert zunächst mit einer bestimmten Schrittgröße und sortiert dann mit einer bestimmten Schrittgröße weiter. Der endgültige Algorithmus sortiert mit einer Schrittgröße von 1. Wenn die Schrittgröße 1 beträgt, wechselt der Algorithmus zur Einfügungssortierung, wodurch sichergestellt wird, dass die Daten sortiert werden. Donald Shell schlug zunächst vor, eine Schrittgröße von frac{n}{2} zu wählen und die Schrittgröße zu halbieren, bis die Schrittgröße 1 erreicht. Obwohl dieser Ansatz besser sein kann als mathcal{O}(n^2)-ähnliche Algorithmen (Einfügungssortierung), gibt es immer noch Raum für die Reduzierung der Durchschnittszeit und der schlechtesten Zeit.

Beispiel für Hill-Sortierung: ein Array von n=10 58 27 32 93 65 87 58 46 9 65, mit einer Schrittgröße von n/2.

Der erste Sortierschritt ist 10/2 = 5

58 27 32 93 65 87 58 46 9 65
1A 1B
2A 2B
3A 3B
4A 4B
5A 5B

Gruppieren Sie zunächst die Reihenfolge der zu sortierenden Elemente mit 5 als Schrittgröße, (1A,1B), (2A,2B), (3A,3B) usw Als Gruppierungszeichen geben Großbuchstaben an, um welches Element der Gruppe es sich handelt, und Zahlen mit derselben Nummer zeigen an, dass sie sich in derselben Gruppe befinden. Daher werden sie in 5 Gruppen unterteilt, nämlich (58,87), (27,58). ), (32,46), (93,9), (65,65) und dann eine direkte Einfügungssortierung für jede Gruppe durchführen. Nach der Sortierung sind die fünf Gruppen (58,87), (27,58), (. 32,46), (9,93), (65, 65), die Gruppensortierung wird nur zur folgenden Tabelle innerhalb jeder Gruppe, das gleiche gilt unten.

Der zweite Sortierschritt ist 5/2 = 2

58 27 32 9 65 87 58 46 93 65

1A 1B

2A 2B

3A 3B

                                           ......

Der dritte Sortierschritt ist 2/2 = 1

32 9 58 27. 5 8 46 65 65 93 87

1A 1B 1C 1D 1E 1F 1G 1H 1I 1J

Der vierte Sortierschritt ist 1/2 = 0, um die geordnete Elementfolge zu erhalten

9 27 32 46 58 58 65 65 87 93

希尔排序的时间性能优于直接插入排序的原因：
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时，n和n2的差别也较小，即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n2)差别不大。
③在希尔排序开始时增量较大，分组较多，每组的记录数目少，故各组内直接插入较快，后来增量di逐渐缩小，分组数逐渐减少，而各组的记录数目逐渐增多，但由于已经按di-1作为距离排过序，使文件较接近于有序状态，所以新的一趟排序过程也较快。

增量序列的选择：Shell排序的执行时间依赖于增量序列。
好的增量序列的共同特征(查到的资料都这么讲)：
① 最后一个增量必须为1；
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。

package cglib;

 

public class StringNumber {
    
    public static void main(String[] args) {

        int[] arr = new int[]{44,33,99,10,30,20,59,78,23,48};

        System.out.print("排序前：");

        for(int o: arr) {

            System.out.print(o+" ");

        }

        System.out.println();

        shellSort(arr);

        System.out.print("排序后：");

        for(int o: arr) {

            System.out.print(o+" ");

        }

        System.out.println();

    }

    private static void shellSort(int[] arr) {

        int j;

        int len = arr.length;

        for(int val=len>>1; val>0; val>>=1) {

            //下面是对本次的所有分组做直接插入排序

            for(int i=val; i<len; i++) {
                System.out.println("for:i="+i);
                System.out.println("for:arr[i]="+arr[i]);
                System.out.println("for:val="+val);
                int temp = arr[i];

                /*

                 * 为什么每次都用temp比较呢？

                 * 因为直接插入就是找到temp的合适位置。

                 * 为什么temp<arr[j-val]这个条件可以放在for内呢？

                 * 因为原来的组内数据已经有序，找到位置就停止便是。

                 *

                 */

                for(j=i; j>=val&&temp<arr[j-val]; j-=val) {
                    System.out.println("er:j="+j);
                    System.out.println("er:arr[j]="+arr[j]);
                    System.out.println("er:j-val="+(j-val));
                    System.out.println("er:arr[j-val]="+arr[j-val]);
                    /*

                     * 为什么是arr[j-val]不是arr[j]呢？

                     * 因为j=i开始的，而且条件是j>=val&&temp<arr[j-val]

                     */

                    arr[j] = arr[j-val];
                    System.out.println("赋值er:arr[j]="+arr[j]);
                }

                /*

                 * 注意不是arr[i] = temp

                 * 直接插入排序也是这样的。

                 * 为什么呢？

                 * 因为j是位置，i是待插入元素

                 */

                arr[j] = temp;

            }

        }

    }
 
}

输出：

排序前：44 33 99 10 30 20 59 78 23 48
for:i=5
for:arr[i]=20
for:val=5
er:j=5
er:arr[j]=20
er:j-val=0
er:arr[j-val]=44
赋值er:arr[j]=44
for:i=6
for:arr[i]=59
for:val=5
for:i=7
for:arr[i]=78
for:val=5
er:j=7
er:arr[j]=78
er:j-val=2
er:arr[j-val]=99
赋值er:arr[j]=99
for:i=8
for:arr[i]=23
for:val=5
for:i=9
for:arr[i]=48
for:val=5
for:i=2
for:arr[i]=78
for:val=2
for:i=3
for:arr[i]=10
for:val=2
er:j=3
er:arr[j]=10
er:j-val=1
er:arr[j-val]=33
赋值er:arr[j]=33
for:i=4
for:arr[i]=30
for:val=2
er:j=4
er:arr[j]=30
er:j-val=2
er:arr[j-val]=78
赋值er:arr[j]=78
for:i=5
for:arr[i]=44
for:val=2
for:i=6
for:arr[i]=59
for:val=2
er:j=6
er:arr[j]=59
er:j-val=4
er:arr[j-val]=78
赋值er:arr[j]=78
for:i=7
for:arr[i]=99
for:val=2
for:i=8
for:arr[i]=23
for:val=2
er:j=8
er:arr[j]=23
er:j-val=6
er:arr[j-val]=78
赋值er:arr[j]=78
er:j=6
er:arr[j]=78
er:j-val=4
er:arr[j-val]=59
赋值er:arr[j]=59
er:j=4
er:arr[j]=59
er:j-val=2
er:arr[j-val]=30
赋值er:arr[j]=30
for:i=9
for:arr[i]=48
for:val=2
er:j=9
er:arr[j]=48
er:j-val=7
er:arr[j-val]=99
赋值er:arr[j]=99
for:i=1
for:arr[i]=10
for:val=1
er:j=1
er:arr[j]=10
er:j-val=0
er:arr[j-val]=20
赋值er:arr[j]=20
for:i=2
for:arr[i]=23
for:val=1
for:i=3
for:arr[i]=33
for:val=1
for:i=4
for:arr[i]=30
for:val=1
er:j=4
er:arr[j]=30
er:j-val=3
er:arr[j-val]=33
赋值er:arr[j]=33
for:i=5
for:arr[i]=44
for:val=1
for:i=6
for:arr[i]=59
for:val=1
for:i=7
for:arr[i]=48
for:val=1
er:j=7
er:arr[j]=48
er:j-val=6
er:arr[j-val]=59
赋值er:arr[j]=59
for:i=8
for:arr[i]=78
for:val=1
for:i=9
for:arr[i]=99
for:val=1
排序后：10 20 23 30 33 44 48 59 78 99

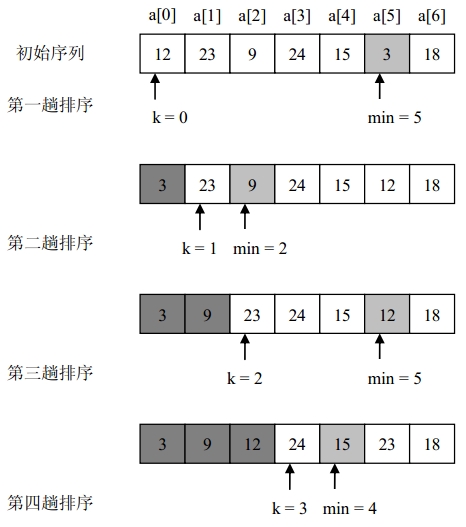
选择排序
每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。

package cglib;

import java.util.Arrays;
import java.util.Date;
import java.util.Random;

public class StringNumber {
    
    public static void main(String[] args){  
        Random random = new Random();  
        int[] array = new int[2000];  
          
          
            for (int j = 0; j < 2000; j++) {  
                array[j] = random.nextInt(100000);  
            }  
        
        System.out.println(Arrays.toString(array));  
        selectSortTest(array);  
        System.out.println(Arrays.toString(array));       
    }  
    
     public static void selectSortTest(int a[]) {  
             
            Date dateStart = new Date();  
            selectSort(a);  
            Date dateEnd = new Date();  
            System.out.println("选择排序耗费时间："  
                    + (dateEnd.getTime() - dateStart.getTime()));  
              
           
        }  
    
    
      
    public static void selectSort(int a[]){  
        int n = a.length;  
        for(int k=0; k<n-1; k++) {  
            int min = k;  
            for(int i=k+1; i<n; i++) {//找出最小值  
                if(a[i] < a[min]) {  
                    min = i;  
                }  
            }  
            if(k != min) {  
                int temp = a[k];  
                a[k] = a[min];  
                a[min] = temp;  
            }  
        }  
    }  
}