 Web-Frontend
Web-Frontend
 js-Tutorial
js-Tutorial
 Warum kann js Dezimaloperationen nicht korrekt verarbeiten? _Javascript-Kenntnisse
Warum kann js Dezimaloperationen nicht korrekt verarbeiten? _Javascript-Kenntnisse
Warum kann js Dezimaloperationen nicht korrekt verarbeiten? _Javascript-Kenntnisse
var sum = 0;
for(var i = 0; i < 10; i++) {
sum += 0.1;
}
console.log(sum);
Wird das obige Programm 1 ausgeben?
Im Artikel 25 JavaScript-Interviewfragen, die Sie kennen müssen erklärt die 8. Frage kurz, warum js Dezimaloperationen nicht korrekt verarbeiten kann. Heute werde ich ein altes Thema noch einmal aufgreifen und dieses Problem eingehender analysieren.
Aber zunächst ist zu beachten, dass die Unfähigkeit, Dezimaloperationen korrekt zu verarbeiten, kein Designfehler in der JavaScript-Sprache selbst ist. Andere höhere Programmiersprachen wie C, Java usw. sind ebenfalls nicht in der Lage um Dezimaloperationen korrekt zu verarbeiten:
#include <stdio.h>
void main(){
float sum;
int i;
sum = 0;
for(i = 0; i < 100; i++) {
sum += 0.1;
}
printf('%f\n', sum); //10.000002
}
Darstellung von Zahlen im Computer
Wir alle wissen, dass in höheren Programmiersprachen geschriebene Programme durch Interpretation, Kompilierung und andere Vorgänge in Maschinensprache umgewandelt werden müssen, die von der CPU (Central Processing Unit) erkannt werden kann, bevor sie ausgeführt werden können Für die CPU werden die dezimalen und dezimalen Zahlensysteme Oktal und Hexadezimal usw. nicht erkannt. Diese im Programm deklarierten Basiszahlen werden zur Berechnung in Binärzahlen umgewandelt.
Warum nicht zur Berechnung in ternäre Zahlen umwandeln?
Das Innere eines Computers besteht aus vielen elektronischen Komponenten wie IC (Integrated Circuit: Integrierter Schaltkreis). Es sieht ungefähr so aus:
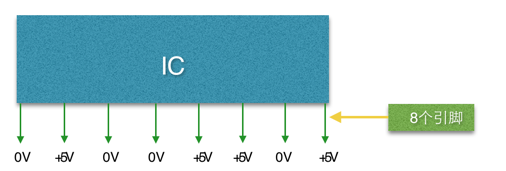
ICs gibt es in vielen Formen, mit vielen Stiften, die nebeneinander auf beiden Seiten oder im Inneren angeordnet sind (im Bild ist nur eine Seite dargestellt). Alle Pins des IC haben nur zwei Zustände der Gleichspannung 0 V oder 5 V, d. h. ein IC-Pin kann nur zwei Zustände darstellen. Diese Eigenschaft von IC bestimmt, dass die Daten im Computer nur mit Binärzahlen verarbeitet werden können.
Da 1 Bit (ein Pin) nur zwei Zustände darstellen kann, lautet die binäre Berechnungsmethode 0, 1, 10, 11, 100 ... Diese Form:
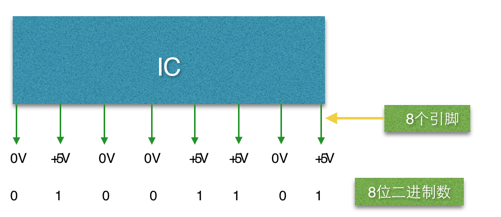
Bei Zahlenoperationen werden also alle Operanden in Binärzahlen umgewandelt, um an der Operation teilzunehmen, z. B. 39, wird in die Binärzahl 00100111 umgewandelt
Binäre Darstellung von Dezimalzahlen
Wie oben erwähnt, werden die Daten im Programm in Binärzahlen umgewandelt, wenn es sich um Dezimalzahlen handelt. Beispielsweise wird die Dezimalzahl 11,1875 in 1101,0010 umgewandelt.
Der numerische Bereich, der durch 4 Nachkommastellen in Binärzahlen ausgedrückt wird, beträgt 0,0000 bis 0,1111. Daher kann dies nur die Kombination (Addition) der vier Dezimalzahlen 0,5, 0,25, 0,125, 0,0625 und die Bitgewichte danach darstellen der Dezimalpunkt. Dezimal:

Wie aus der obigen Tabelle ersichtlich ist, ist die nächste Ziffer der Dezimalzahl 0,0625. Daher können Dezimalzahlen zwischen 0 und 0,0625 nicht durch Binärzahlen mit 4 Nachkommastellen dargestellt werden; der DezimalpunktDie Anzahl der entsprechenden Dezimalstellen erhöht sich ebenfalls, aber egal wie viele Stellen hinzugefügt werden, das Ergebnis von 0,1 kann nicht erhalten werden. Tatsächlich ist 0,1 in Binär umgewandelt 0,00110011001100110011... Beachten Sie, dass 0011 unendlich wiederholt wird:
console.log(0.2+0.1); //操作数的二进制表示 0.1 => 0.0001 1001 1001 1001…(无限循环) 0.2 => 0.0011 0011 0011 0011…(无限循环)
Der Zahlentyp von js ist nicht wie C/Java in Ganzzahl, einfache Genauigkeit, doppelte Genauigkeit usw. unterteilt, sondern wird einheitlich als Gleitkommatyp mit doppelter Genauigkeit ausgedrückt. Gemäß den IEEE-Vorschriften verwenden Gleitkommazahlen mit einfacher Genauigkeit 32 Bit zur Darstellung aller Dezimalzahlen, während Gleitkommazahlen mit doppelter Genauigkeit 64 Bit zur Darstellung aller Dezimalzahlen verwenden. Gleitkommazahlen bestehen aus Vorzeichen, Mantisse, Exponent und Basis , sodass nicht alle Ziffern verwendet werden, müssen Symbole, Exponenten usw. auch Ziffern belegen, und die Basis belegt keine Ziffern:

Der Dezimalteil einer Gleitkommazahl mit doppelter Genauigkeit unterstützt bis zu 52 Ziffern, sodass Sie nach der Addition der beiden eine Zeichenfolge von 0,0100110011001100110011001100110011001100 erhalten ... eine Binärzahl, die aufgrund der Beschränkung der Dezimalstelle von gekürzt wird Konvertieren Sie die Gleitkommazahl zu diesem Zeitpunkt in eine Dezimalzahl. Das ergibt 0,30000000000000004.
Zusammenfassung
js kann Dezimaloperationen nicht korrekt verarbeiten, einschließlich anderer höherer Programmiersprachen. Dies ist jedoch kein Designfehler der Sprache selbst, aber der Computer selbst kann Dezimaloperationen häufig nicht korrekt verarbeiten Dezimalbrüche können binär dargestellt werden.
Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, er wird für das Studium aller hilfreich sein.

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1389
1389
 52
52
 So verwenden Sie JS und Baidu Maps, um die Kartenschwenkfunktion zu implementieren
Nov 21, 2023 am 10:00 AM
So verwenden Sie JS und Baidu Maps, um die Kartenschwenkfunktion zu implementieren
Nov 21, 2023 am 10:00 AM
So implementieren Sie die Kartenschwenkfunktion mit JS und Baidu Map. Baidu Map ist eine weit verbreitete Kartendienstplattform, die häufig zur Anzeige geografischer Informationen, Positionierung und anderer Funktionen in der Webentwicklung verwendet wird. In diesem Artikel wird erläutert, wie Sie mit JS und der Baidu Map API die Kartenschwenkfunktion implementieren, und es werden spezifische Codebeispiele bereitgestellt. 1. Vorbereitung Bevor Sie die Baidu Map API nutzen können, müssen Sie zunächst ein Entwicklerkonto auf der Baidu Map Open Platform (http://lbsyun.baidu.com/) beantragen und eine Anwendung erstellen. Erstellung abgeschlossen
 Empfohlen: Ausgezeichnetes JS-Open-Source-Projekt zur Gesichtserkennung und -erkennung
Apr 03, 2024 am 11:55 AM
Empfohlen: Ausgezeichnetes JS-Open-Source-Projekt zur Gesichtserkennung und -erkennung
Apr 03, 2024 am 11:55 AM
Die Technologie zur Gesichtserkennung und -erkennung ist bereits eine relativ ausgereifte und weit verbreitete Technologie. Derzeit ist JS die am weitesten verbreitete Internetanwendungssprache. Die Implementierung der Gesichtserkennung und -erkennung im Web-Frontend hat im Vergleich zur Back-End-Gesichtserkennung Vor- und Nachteile. Zu den Vorteilen gehören die Reduzierung der Netzwerkinteraktion und die Echtzeiterkennung, was die Wartezeit des Benutzers erheblich verkürzt und das Benutzererlebnis verbessert. Die Nachteile sind: Es ist durch die Größe des Modells begrenzt und auch die Genauigkeit ist begrenzt. Wie implementiert man mit js die Gesichtserkennung im Web? Um die Gesichtserkennung im Web zu implementieren, müssen Sie mit verwandten Programmiersprachen und -technologien wie JavaScript, HTML, CSS, WebRTC usw. vertraut sein. Gleichzeitig müssen Sie auch relevante Technologien für Computer Vision und künstliche Intelligenz beherrschen. Dies ist aufgrund des Designs der Webseite erwähnenswert
 So erstellen Sie ein Aktien-Candlestick-Diagramm mit PHP und JS
Dec 17, 2023 am 08:08 AM
So erstellen Sie ein Aktien-Candlestick-Diagramm mit PHP und JS
Dec 17, 2023 am 08:08 AM
So verwenden Sie PHP und JS zum Erstellen eines Aktienkerzendiagramms. Ein Aktienkerzendiagramm ist eine gängige technische Analysegrafik auf dem Aktienmarkt. Es hilft Anlegern, Aktien intuitiver zu verstehen, indem es Daten wie den Eröffnungskurs, den Schlusskurs, den Höchstkurs usw niedrigster Preis der Aktie. In diesem Artikel erfahren Sie anhand spezifischer Codebeispiele, wie Sie Aktienkerzendiagramme mit PHP und JS erstellen. 1. Vorbereitung Bevor wir beginnen, müssen wir die folgende Umgebung vorbereiten: 1. Ein Server, auf dem PHP 2. Ein Browser, der HTML5 und Canvas 3 unterstützt
 Wesentliche Tools für die Aktienanalyse: Lernen Sie die Schritte zum Zeichnen von Kerzendiagrammen mit PHP und JS
Dec 17, 2023 pm 06:55 PM
Wesentliche Tools für die Aktienanalyse: Lernen Sie die Schritte zum Zeichnen von Kerzendiagrammen mit PHP und JS
Dec 17, 2023 pm 06:55 PM
Wesentliche Tools für die Aktienanalyse: Lernen Sie die Schritte zum Zeichnen von Kerzendiagrammen in PHP und JS. Mit der rasanten Entwicklung des Internets und der Technologie ist der Aktienhandel für viele Anleger zu einer wichtigen Möglichkeit geworden. Die Aktienanalyse ist ein wichtiger Teil der Anlegerentscheidung, und Kerzendiagramme werden häufig in der technischen Analyse verwendet. Wenn Sie lernen, wie man Kerzendiagramme mit PHP und JS zeichnet, erhalten Anleger intuitivere Informationen, die ihnen helfen, bessere Entscheidungen zu treffen. Ein Candlestick-Chart ist ein technischer Chart, der Aktienkurse in Form von Candlesticks anzeigt. Es zeigt den Aktienkurs
 So verwenden Sie JS und Baidu Map, um die Funktion zur Verarbeitung von Kartenklickereignissen zu implementieren
Nov 21, 2023 am 11:11 AM
So verwenden Sie JS und Baidu Map, um die Funktion zur Verarbeitung von Kartenklickereignissen zu implementieren
Nov 21, 2023 am 11:11 AM
Überblick über die Verwendung von JS und Baidu Maps zum Implementieren von Funktionen zur Verarbeitung von Kartenklickereignissen: In der Webentwicklung ist es häufig erforderlich, Kartenfunktionen zum Anzeigen des geografischen Standorts und geografischer Informationen zu verwenden. Die Verarbeitung von Klickereignissen auf der Karte ist ein häufig verwendeter und wichtiger Teil der Kartenfunktion. In diesem Artikel wird erläutert, wie Sie mithilfe von JS und der Baidu-Karten-API die Klickereignisverarbeitungsfunktion der Karte implementieren, und es werden spezifische Codebeispiele angegeben. Schritte: Importieren Sie die API-Datei von Baidu Map. Importieren Sie zunächst die Datei von Baidu Map API in die HTML-Datei.
 So verwenden Sie JS und Baidu Maps, um die Karten-Heatmap-Funktion zu implementieren
Nov 21, 2023 am 09:33 AM
So verwenden Sie JS und Baidu Maps, um die Karten-Heatmap-Funktion zu implementieren
Nov 21, 2023 am 09:33 AM
Verwendung von JS und Baidu Maps zur Implementierung der Karten-Heatmap-Funktion Einführung: Mit der rasanten Entwicklung des Internets und mobiler Geräte sind Karten zu einem häufigen Anwendungsszenario geworden. Als visuelle Darstellungsmethode können Heatmaps uns helfen, die Verteilung von Daten intuitiver zu verstehen. In diesem Artikel wird die Verwendung von JS und der Baidu Map API zur Implementierung der Karten-Heatmap-Funktion vorgestellt und spezifische Codebeispiele bereitgestellt. Vorbereitung: Bevor Sie beginnen, müssen Sie Folgendes vorbereiten: ein Baidu-Entwicklerkonto, eine Anwendung erstellen und den entsprechenden AP erhalten
 PHP- und JS-Entwicklungstipps: Beherrschen Sie die Methode zum Zeichnen von Aktienkerzendiagrammen
Dec 18, 2023 pm 03:39 PM
PHP- und JS-Entwicklungstipps: Beherrschen Sie die Methode zum Zeichnen von Aktienkerzendiagrammen
Dec 18, 2023 pm 03:39 PM
Mit der rasanten Entwicklung der Internetfinanzierung sind Aktieninvestitionen für immer mehr Menschen zur Wahl geworden. Im Aktienhandel sind Kerzendiagramme eine häufig verwendete Methode der technischen Analyse. Sie können den sich ändernden Trend der Aktienkurse anzeigen und Anlegern helfen, genauere Entscheidungen zu treffen. In diesem Artikel werden die Entwicklungskompetenzen von PHP und JS vorgestellt, der Leser wird zum Verständnis des Zeichnens von Aktienkerzendiagrammen geführt und es werden spezifische Codebeispiele bereitgestellt. 1. Aktien-Kerzendiagramme verstehen Bevor wir uns mit dem Zeichnen von Aktien-Kerzendiagrammen befassen, müssen wir zunächst verstehen, was ein Kerzendiagramm ist. Candlestick-Charts wurden von den Japanern entwickelt
 So verwenden Sie JS und Baidu Maps, um die Funktion zum Zeichnen von Kartenpolygonen zu implementieren
Nov 21, 2023 am 10:53 AM
So verwenden Sie JS und Baidu Maps, um die Funktion zum Zeichnen von Kartenpolygonen zu implementieren
Nov 21, 2023 am 10:53 AM
Verwendung von JS und Baidu Maps zur Implementierung der Kartenpolygonzeichnungsfunktion In der modernen Webentwicklung sind Kartenanwendungen zu einer der häufigsten Funktionen geworden. Durch das Zeichnen von Polygonen auf der Karte können wir bestimmte Bereiche markieren, damit Benutzer sie anzeigen und analysieren können. In diesem Artikel wird erläutert, wie Sie mithilfe von JS und der Baidu-Karten-API die Funktion zum Zeichnen von Kartenpolygonen implementieren, und es werden spezifische Codebeispiele bereitgestellt. Zuerst müssen wir die Baidu Map API einführen. Mit dem folgenden Code können Sie das JavaScript der Baidu Map API in eine HTML-Datei importieren



