1. Stapel
Ein Stapel ist eine Tabelle, die Einfüge- und Löschvorgänge auf nur eine Stelle beschränkt. Dieser Ort ist das Ende der Tabelle und wird als oberste Stelle des Stapels bezeichnet. Die Grundoperationen des Stapels sind PUSH (in den Stapel) und POP (in den Stapel). Der Stapel wird auch als LIFO-Tabelle (Last In, First Out) bezeichnet.
1.1 Stack-Implementierung
class Stack(object):
def __init__(self):
self.stack=[]
def isEmpty(self):
return self.stack==[]
def push(self,item):
self.stack.append(item)
def pop(self):
if self.isEmpty():
raise IndexError,'pop from empty stack'
return self.stack.pop()
def peek(self):
return self.stack[-1]
def size(self):
return len(self.stack)1.2 Stack-Anwendung
1.2.1 Überprüfen Sie die gepaarten Symbole im Programm
Die Syntaxfehler des Programms sind Wird häufig durch ein fehlendes Symbol verursacht. Mithilfe des Stapels kann überprüft werden, ob Symbole gepaart sind. Erstellen Sie einen leeren Stapel. Wenn das Zeichen ein offenes Symbol ist ('({[')), schieben Sie es auf den Stapel. Wenn das Symbol ein geschlossenes Symbol ist (')]}'), wird beim Stapeln ein Fehler gemeldet ist leer, was dem Fehler „()}“ entspricht. Andernfalls wird der Stapel geöffnet. Wenn das geöffnete Symbol nicht das entsprechende offene Symbol ist, wird ein Fehler gemeldet, der dem Fehler von „(}“ entspricht. Wenn der Stapel am Ende leer ist, wird ein Fehler angezeigt gemeldet, entsprechend dem Fehler von '({}'.
def match(i,j):
opens='([{'
closes=')]}'
return opens.index(i)==closes.index(j)
def syntaxChecker(string):
stack=Stack()
balanced=True
for i in string:
if i in '([{':
stack.push(i)
elif i in ')]}':
if stack.isEmpty():
balanced=False
break
else:
j=stack.pop()
if not match(j,i):
balanced=False
break
if not stack.isEmpty():
balanced=False
return balanced1.2.2 Dezimalkonvertierung
Dezimalkonvertierung in Binärzahl: Dezimalzahl in Binärzahl umwandeln, bis der Quotient 0 ist. Beginnen Sie mit dem Lesen Von der unteren linken Zahl, dann lesen Sie die rechte Zahl, beginnend mit Lesen Sie unten
Von Problemlösung mit Algorithmen und Bild „Datenstrukturen“:
Code:
def decimal_to_bin(dec):
stack=Stack()
cur=dec
while cur>0:
a=cur%2
cur=cur/2
stack.push(a)
binstr=''
while not stack.isEmpty():
binstr+=str(stack.pop())
return binstr1.2.3 Suffix-Notation
Die Postfix-Notation (Postfix) verwendet einen Stapel. Wenn sie eine Zahl sieht, wird sie in den Stapel verschoben. Wenn sie auf einen Operator trifft, wirkt sie auf die beiden aus dem Stapel entnommenen Elemente und legt das Ergebnis in den Stapel.
(7+8)/(3+2) kann geschrieben werden als 7 8 + 3 2 + /
Bild aus „Problemlösung mit Algorithmen und Datenstrukturen“:
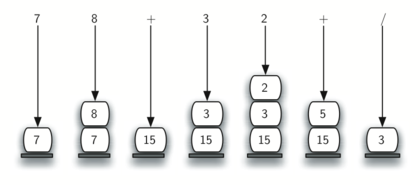
Konvertierung von Infix zu Suffix: Wenn ein Operand gelesen wird, fügen Sie ihn in die Ausgabe ein. Wenn der Operator (+,-,*,/) gelesen wird und der Stapel leer ist, wird er in den Stapel verschoben. Andernfalls wird das Stapelelement entfernt und in die Ausgabe eingefügt, bis ein Element mit einer niedrigeren Priorität gefunden wird. Nachdem Sie „(“ gelesen haben, schieben Sie es auf den Stapel, und wenn Sie „)“ lesen, packen Sie die Stapelelemente ein und senden Sie sie an die Ausgabe, bis „(“ gefunden wird. Am Ende schieben Sie die Stapelelemente hinein, bis der Stapel leer ist.
Bilder aus „Problemlösung mit Algorithmen und Datenstrukturen“:
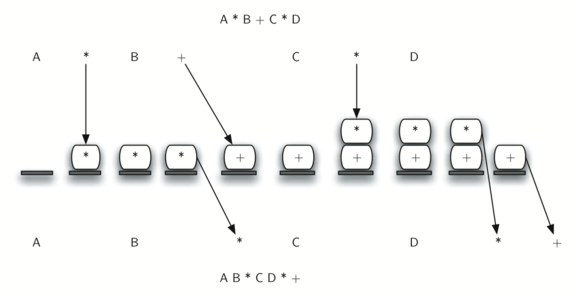
def infixtoPostfix(infix):
a={}
a['*']=3
a['/']=3
a['+']=2
a['-']=2
a['(']=1
stack=Stack()
post=''
for i in infix:
if i not in a and i!=')':
post+=i
elif i=='(':
stack.push(i)
elif i==')':
top=stack.pop()
while top!='(':
post+=top
top=stack.pop()
else:
while not stack.isEmpty() and a[i]<=a[stack.peek()]:
post+=stack.pop()
stack.push(i)
while not stack.isEmpty():
post+=stack.pop()
return post
def postfixExp(postfix):
stack=Stack()
postlist=postfix.split()
for i in postlist:
if i not in '+-*/':
stack.push(i)
else:
a=stack.pop()
b=stack.pop()
result=math(i,b,a)
stack.push(result)
return stack.pop()
def math(x,y,z):
if x=='+':
return float(y)+float(z)
if x=='-':
return float(y)-float(z)
if x=='*':
return float(y)*float(z)
if x=='/':
return float(y)/float(z)2 Queue
Queue (Warteschlange) ist auch dabei Eine Tabelle, verwenden Sie die Warteschlange. Das Einfügen und Löschen erfolgt an verschiedenen Enden. Die Grundoperationen der Warteschlange sind Enqueue (enqueue), wodurch ein Element am Ende der Tabelle (hinten) eingefügt wird, und dequeue (Dequeue), wodurch das Element gelöscht wird am Anfang der Tabelle. 🎜>
Das Obige ist der Inhalt der Python-Datenstruktur – Implementierung von Stapel und Warteschlange (1). Weitere verwandte Artikel finden Sie auf der chinesischen PHP-Website (www.php.cn). )class Queue(object):
def __init__(self):
self.queue=[]
def isEmpty(self):
return self.queue==[]
def enqueue(self,x):
self.queue.append(x)
def dequeue(self):
if self.queue:
a=self.queue[0]
self.queue.remove(a)
return a
else:
raise IndexError,'queue is empty'
def size(self):
return len(self.queue)
