Sieben Möglichkeiten, den allgemeinen Begriff der Fibonacci-Folge zu realisieren

1: Rekursive Implementierung
Verwenden Sie die Formel f[n]=f[n-1]+f[n-2] und berechnen Sie rekursiv nacheinander. Die rekursive Endbedingung ist f[1]=1, f[2] =1.
Zweitens: Array-Implementierung
Die Raumkomplexität und die Zeitkomplexität sind beide 0(n), die Effizienz ist durchschnittlich und sie ist schneller als die Rekursion.
Drei: Vektor-Implementierung
Die Zeitkomplexität ist 0(1) und ich weiß natürlich nicht, ob der Vektor effizient ist seine eigenen Attribute, die Ressourcen belegen.
Viertens: Queue-Implementierung
Natürlich eignen sich Warteschlangen besser für die Implementierung von Fibonacci-Sequenzen als Arrays. Die zeitliche Komplexität und die räumliche Komplexität sind die gleichen wie bei vector, aber Warteschlangen sind dafür perfekt 🎜> f(n)=f(n-1)+f(n-2), f(n) bezieht sich nur auf f(n-1) und f(n-2), nachdem f(n) eintritt Warteschlange, f( n-2) kann aus der Warteschlange entfernt werden.
Fünftens: Iterative Implementierung
Die iterative Implementierung ist am effizientesten, mit einer Zeitkomplexität von 0(n) und einer räumlichen Komplexität von 0(1).
Sechs: Formelimplementierung
Als ich Baidu durchsuchte, entdeckte ich, dass die Fibonacci-Folge eine Formel hat, sodass sie mithilfe der Formel berechnet werden kann.
Da die Genauigkeit des Doppeltyps nicht ausreicht, weisen die vom Programm berechneten Ergebnisse Fehler auf. Wenn die Formel erweitert und berechnet wird, ist das Ergebnis korrekt.
Der vollständige Implementierungscode lautet wie folgt:

#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index)     //递归实现
{
 if(index<1)
 {
  return -1;
 }
 if(index==1 || index==2)
  return 1;
 return fib1(index-1)+fib1(index-2);
}
int fib2(int index)     //数组实现
{
 if(index<1)
 {
  return -1;
 }
 if(index<3)
 {
  return 1;
 }
 int *a=new int[index];
 a[0]=a[1]=1;
 for(int i=2;i<index;i++)
  a[i]=a[i-1]+a[i-2];
 int m=a[index-1];
 delete a;         //释放内存空间
 return m;
}
int fib3(int index)           //借用vector<int>实现
{
 if(index<1)
 {
  return -1;
 }
 vector<int> a(2,1);      //创建一个含有2个元素都为1的向量
 a.reserve(3);
 for(int i=2;i<index;i++)
 {
  a.insert(a.begin(),a.at(0)+a.at(1));
  a.pop_back();
 }
 return a.at(0);
} 
int fib4(int index)       //队列实现
{
 if(index<1)
 {
  return -1;
 }
 queue<int>q;
 q.push(1);
 q.push(1);
 for(int i=2;i<index;i++)
 {
  q.push(q.front()+q.back());
  q.pop();
 }
 return q.back();
}
int fib5(int n)          //迭代实现
{
 int i,a=1,b=1,c=1;
 if(n<1)
 {
  return -1;
 }
 for(i=2;i<n;i++)
 {
  c=a+b;     //辗转相加法（类似于求最大公约数的辗转相除法）
  a=b;
  b=c;
 }
 return c;
}
int fib6(int n)
{
 double gh5=sqrt((double)5);
 return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
} 
int main(void)
{
 printf("%d\n",fib3(6));
 system("pause");
 return 0;
}

Sieben: Bipartite-Matrix-Methode

Wie oben gezeigt, jedes Element in der Fibonacci-Sequenz kann als Matrix verwendet werden. Potenzen können berechnet werden, und die n-te Potenz kann in Logn-Zeit berechnet werden.

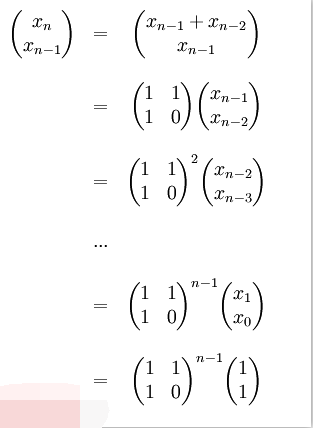
Der Code ist unten gepostet:

void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
 int tmp[4];
 tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
 tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
 tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
 tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
 c[0][0]=tmp[0]%mod;
 c[0][1]=tmp[1]%mod;
 c[1][0]=tmp[2]%mod;
 c[1][1]=tmp[3]%mod;
}//计算矩阵乘法，c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
 if(n==0)return 0;
 else if(n<=2)return 1;//这里表示第0项为0，第1，2项为1
 int a[2][2]={{1,1},{1,0}};
 int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
 int s;
 n-=2;
 while(n>0)
 {
  if(n%2 == 1)
   multiply(result,result,a,mod);
  multiply(a,a,a,mod);
  n /= 2;
 }//二分法求矩阵幂
 s=(result[0][0]+result[0][1])%mod;//结果
 return s;
}

Anbei ist die Halbierungsmethode zur Berechnung der n-ten Potenzfunktion von a.

int pow(int a,int n)
{
 int ans=1;
 while(n)
 {
  if(n&1)
   ans*=a;
  a*=a;
  n>>=1;
 }
 return ans;
}

Weitere verwandte Artikel zu den sieben Implementierungsmethoden zum Ermitteln des allgemeinen Termes der Fibonacci-Folge finden Sie auf der chinesischen PHP-Website!