
Zusammenfassung
Dieser Artikel verwendet die MySQL-Datenbank als Forschungsobjekt und erörtert einige Themen im Zusammenhang mit Datenbankindizes. Es ist zu beachten, dass MySQL viele Speicher-Engines unterstützt und verschiedene Speicher-Engines unterschiedliche Indizes unterstützen. Daher unterstützt die MySQL-Datenbank mehrere Indextypen, wie z. B. BTree-Index, Hash-Index, Volltextindex usw. Um Verwirrung zu vermeiden, konzentriert sich dieser Artikel nur auf den BTree-Index, da dies der Index ist, der hauptsächlich bei der Verwendung von MySQL behandelt wird. Auf den Hash-Index und den Volltextindex wird in diesem Artikel zunächst nicht eingegangen Sein.
Der Hauptinhalt des Artikels ist in drei Teile gegliedert.
Im ersten Teil werden hauptsächlich die mathematischen Grundlagen des MySQL-Datenbankindex auf der theoretischen Ebene der Datenstruktur und des Algorithmus erörtert.
Im zweiten Teil werden Themen wie Clustered-Indizes, Nicht-Clustered-Indizes und das Abdecken von Indizes basierend auf der Architekturimplementierung von Indizes in den Datenspeicher-Engines MyISAM und InnoDB in der MySQL-Datenbank erörtert.
Der dritte Teil diskutiert die Strategie der Hochleistungsindexnutzung in MySQL basierend auf der oben genannten theoretischen Grundlage.
Grundlagen von Datenstrukturen und Algorithmen
Das Wesen des Index
MySQLs offizielle Definition von Index lautet: Index (Index) ist eine Datenstruktur, die MySQL dabei hilft, Daten effizient zu erhalten. Durch Extrahieren des Satzstamms können Sie die Essenz des Index ermitteln: Der Index ist eine Datenstruktur.
Wir wissen, dass die Datenbankabfrage eine der wichtigsten Funktionen der Datenbank ist. Wir alle möchten Daten so schnell wie möglich abfragen, daher optimieren Designer von Datenbanksystemen die Abfragealgorithmen aus Sicht. Der grundlegendste Abfragealgorithmus ist natürlich die lineare Suche. Dieser Algorithmus mit einer Komplexität von O(n) ist offensichtlich schlecht, wenn die Datenmenge groß ist. Glücklicherweise hat die Entwicklung der Informatik viele bessere Suchalgorithmen hervorgebracht Suche, Binärbaumsuche usw. Wenn Sie eine kleine Analyse durchführen, werden Sie feststellen, dass jeder Suchalgorithmus nur auf eine bestimmte Datenstruktur angewendet werden kann. Beispielsweise erfordert die binäre Suche, dass die abgerufenen Daten geordnet sind, während die binäre Baumsuche nur auf binäre Suchbäume angewendet werden kann. Aber die Daten selbst Die Organisationsstruktur kann verschiedene Datenstrukturen nicht vollständig erfüllen (z. B. ist es theoretisch unmöglich, beide Spalten gleichzeitig in der richtigen Reihenfolge zu organisieren). Daher verwaltet das Datenbanksystem zusätzlich zu den Daten auch Datenstrukturen, die bestimmte Anforderungen erfüllen Suchalgorithmen verweisen in irgendeiner Weise auf Daten, sodass erweiterte Suchalgorithmen auf diesen Datenstrukturen implementiert werden können. Diese Datenstruktur ist ein Index.
Sehen Sie sich ein Beispiel an:
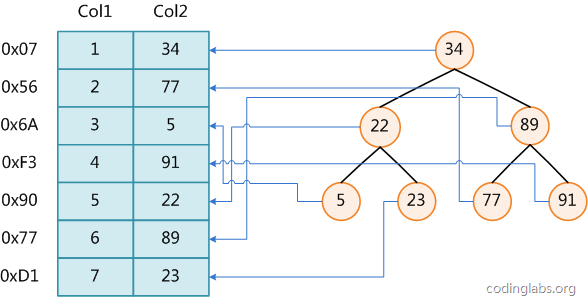
Abbildung 1
Abbildung 1 zeigt eine mögliche Indizierungsmethode. Auf der linken Seite befindet sich eine Datentabelle mit insgesamt zwei Spalten und sieben Datensätzen. Die Spalte ganz links ist die physische Adresse des Datensatzes (beachten Sie, dass logisch benachbarte Datensätze nicht unbedingt physisch benachbart auf der Festplatte liegen). Um die Suche nach Col2 zu beschleunigen, können Sie wie rechts gezeigt einen binären Suchbaum verwalten, der den Indexschlüsselwert und einen Zeiger auf die physische Adresse des entsprechenden Datensatzes enthält Binäre Suche in O(log2n) Die entsprechenden Daten werden innerhalb der Komplexität erhalten.
Obwohl es sich um einen echten Index handelt, werden tatsächliche Datenbanksysteme fast nie mit binären Suchbäumen oder deren weiterentwickelten Varianten, den Rot-Schwarz-Bäumen, implementiert. Die Gründe dafür werden weiter unten erläutert.
B-Tree und B+Tree
Derzeit verwenden die meisten Datenbanksysteme und Dateisysteme B-Tree oder seine Variante B+Tree als Indexstruktur, die im nächsten Abschnitt kombiniert wird In diesem Artikel wird erläutert, warum B-Tree und B+Tree bei der Indizierung so weit verbreitet sind. In diesem Abschnitt werden sie zunächst ausschließlich aus der Perspektive der Datenstruktur beschrieben.
B-Baum
Um B-Baum zu beschreiben, definieren Sie zunächst einen Datensatz als Tupel [Schlüssel, Daten]. Schlüssel ist der Schlüsselwert des Datensatzes für verschiedene Datensätze , Schlüssel unterscheiden sich voneinander; Daten sind der Datensatz mit Ausnahme des Schlüssels. Dann ist B-Tree eine Datenstruktur, die die folgenden Bedingungen erfüllt:
1. d ist eine positive ganze Zahl größer als 1, was als Grad des B-Baums bezeichnet wird.
2. h ist eine positive ganze Zahl, die als Höhe des B-Baums bezeichnet wird.
3. Jeder Nicht-Blattknoten besteht aus n-1 Schlüsseln und n Zeigern, wobei d
4. Jeder Blattknoten enthält mindestens einen Schlüssel und zwei Zeiger und höchstens 2d-1-Schlüssel und 2d-Zeiger.
5. Alle Blattknoten haben die gleiche Tiefe, die der Baumhöhe h entspricht.
6. Der Schlüssel und der Zeiger sind voneinander beabstandet, und die beiden Enden des Knotens sind Zeiger.
7. Die Schlüssel in einem Knoten sind von links nach rechts nicht abnehmend angeordnet.
8. Alle Knoten bilden eine Baumstruktur.
9. Jeder Zeiger ist entweder null oder zeigt auf einen anderen Knoten.
10. Wenn sich ein Zeiger ganz links vom Knoten befindet und nicht null ist, sind alle Schlüssel, die er auf den Knoten zeigt, kleiner als v(key1), wobei v(key1) der Wert von ist der erste Schlüssel des Knotens.
11. Wenn sich ein Zeiger auf der äußersten rechten Seite des Knotens befindet und nicht null ist, sind alle Schlüssel, die er auf den Knoten zeigt, größer als v(keym), wobei v(keym) der Wert von ist der letzte Schlüssel des Knotens.
12. Wenn die benachbarten Schlüssel links und rechts eines Zeigers keyi bzw. keyi+1 sind und nicht null sind, dann sind alle Schlüssel, die auf den Knoten zeigen, kleiner als v(keyi+1) und größer als v(keyi).
Abbildung 2 ist ein schematisches Diagramm eines B-Baums mit d=2.
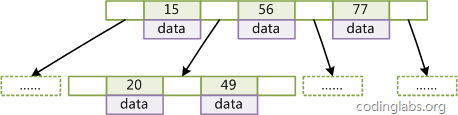
Abbildung 2
Aufgrund der Eigenschaften von B-Tree ist der Algorithmus zum Abrufen von Daten per Schlüssel in B-Tree sehr intuitiv: Führen Sie zunächst eine binäre Suche durch Wenn der Wurzelknoten gefunden wird, werden die Daten des entsprechenden Knotens zurückgegeben. Andernfalls wird der Knoten, auf den der Zeiger des entsprechenden Intervalls zeigt, rekursiv durchsucht, bis der Knoten gefunden wird oder der Nullzeiger gefunden wird , und die letztere Suche schlägt fehl. Der Pseudocode des Suchalgorithmus auf B-Tree lautet wie folgt:
BTree_Search(node, key)
{
if(node == null) return null;
foreach(node.key)
{
if(node.key[i] == key) return node.data[i];
if(node.key[i] > key) return BTree_Search(point[i]->node);
}
return BTree_Search(point[i+1]->node);
}
data = BTree_Search(root, my_key);Es gibt eine Reihe interessanter Eigenschaften über B-Tree, zum Beispiel, wenn ein B-Baum mit Grad d N Schlüssel hat sein Index, dann sein Baum. Die Obergrenze für hohes h ist logd((N+1)/2). Um einen Schlüssel abzurufen, beträgt die asymptotische Komplexität der Ermittlung der Anzahl der Knoten O(logdN). An diesem Punkt ist ersichtlich, dass B-Tree eine sehr effiziente Indexdatenstruktur ist.
Da außerdem das Einfügen und Löschen neuer Datensätze die Eigenschaften des B-Baums zerstört, muss der Baum beim Einfügen und Löschen geteilt, zusammengeführt, übertragen usw. werden, um die Eigenschaften des B-Baums beizubehalten. In diesem Artikel möchte ich den Inhalt von B-Tree nicht vollständig diskutieren, da es bereits viele Materialien gibt, die die mathematischen Eigenschaften sowie die Einfüge- und Löschalgorithmen von B-Tree detailliert beschreiben. Interessierte Freunde können die entsprechenden Materialien in der Referenz finden Spalte am Ende dieses Artikels zum Lesen.
B+Tree
Es gibt viele Varianten von B-Tree, die häufigste davon ist B+Tree. Beispielsweise verwendet MySQL im Allgemeinen B+Tree, um seine Indexstruktur zu implementieren.
Im Vergleich zu B-Tree weist B+Tree die folgenden Unterschiede auf:
1 Die Obergrenze des Zeigers jedes Knotens beträgt 2d statt 2d+1.
2. Interne Knoten speichern keine Daten, nur Schlüssel speichern keine Zeiger.
Abbildung 3 ist ein einfaches B+Baum-Diagramm.
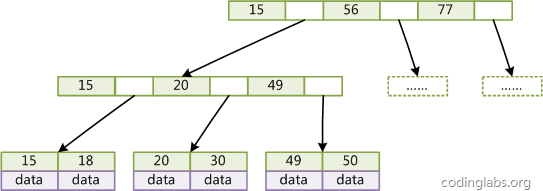
Abbildung 3
Da nicht alle Knoten die gleiche Domäne haben, haben Blattknoten und interne Knoten in B+Tree im Allgemeinen unterschiedliche Größen. Dies unterscheidet sich von B-Tree. Obwohl die Anzahl der in verschiedenen Knoten in B-Tree gespeicherten Schlüssel und Zeiger inkonsistent sein kann, sind die Domäne und die Obergrenze jedes Knotens konsistent. Daher gilt B-Tree in der Implementierung häufig gleichermaßen die Größe jedes Knotens.
Im Allgemeinen eignet sich B+Tree besser für die Implementierung einer externen Speicherindexstruktur als B-Tree. Die spezifischen Gründe hängen mit dem Prinzip des externen Speichers und des Computerzugriffs zusammen, die im Folgenden erläutert werden.
B+Tree mit sequentiellen Zugriffszeigern
Die in Datenbanksystemen oder Dateisystemen allgemein verwendete B+Tree-Struktur wurde auf Basis des klassischen B+Tree optimiert und um sequentielle Zugriffszeiger erweitert.
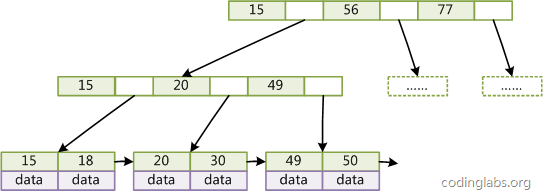
Abbildung 4
Fügen Sie, wie in Abbildung 4 gezeigt, in jedem Blattknoten von B+Tree einen Zeiger auf den benachbarten Blattknoten hinzu, um A B+ zu bilden Baum mit sequentiellen Zugriffszeigern. Der Zweck dieser Optimierung besteht darin, die Leistung des Intervallzugriffs zu verbessern. Wenn Sie beispielsweise in Abbildung 4 alle Datensätze mit Schlüsseln von 18 bis 49 abfragen möchten, müssen Sie nach dem Finden von 18 nur die Knoten und Zeiger nacheinander durchlaufen um auf alle Datenknoten gleichzeitig zuzugreifen, was die Effizienz der Intervallabfrage erheblich verbessert.
Dieser Abschnitt gibt eine kurze Einführung in B-Tree und B+Tree. Der nächste Abschnitt kombiniert die Prinzipien des Speicherzugriffs, um vorzustellen, warum B+Tree derzeit die bevorzugte Datenstruktur für die Indizierung in Datenbanksystemen ist.
Warum B-Tree (B+Tree) verwenden
Wie oben erwähnt, können Datenstrukturen wie Rot-Schwarz-Bäume auch zum Implementieren von Indizes verwendet werden, Dateisysteme und Datenbanksysteme verwenden dies jedoch im Allgemeinen B-/+Tree wird als Indexstruktur verwendet. In diesem Abschnitt wird die theoretische Grundlage von B-/+Tree als Index erörtert, die auf Kenntnissen über Computerkompositionsprinzipien basiert.
Im Allgemeinen ist auch der Index selbst sehr groß und kann nicht vollständig im Speicher gespeichert werden. Daher wird der Index häufig in Form einer Indexdatei auf der Festplatte gespeichert. In diesem Fall wird während des Indexsuchvorgangs ein Festplatten-E/A-Verbrauch erzeugt, der um mehrere Größenordnungen höher ist. Dies ist der wichtigste Indikator für die Bewertung der Datenqualität Die Struktur als Index ist die asymptotische Komplexität der Anzahl der Festplatten-E/A-Vorgänge während des Suchvorgangs. Mit anderen Worten: Die strukturelle Organisation des Index sollte die Anzahl der Festplatten-E/A-Zugriffe während des Suchvorgangs minimieren. Im Folgenden werden zunächst die Prinzipien des Speicher- und Festplattenzugriffs vorgestellt und anschließend die Effizienz von B-/+Tree als Index basierend auf diesen Prinzipien analysiert.
Prinzipien des Hauptspeicherzugriffs
Der derzeit in Computern verwendete Hauptspeicher ist im Wesentlichen ein zufälliger Lese-/Schreibspeicher (RAM). Dieser Artikel wird beschrieben Ignorieren Sie die spezifischen Unterschiede und abstrahieren Sie ein sehr einfaches Zugriffsmodell, um das Funktionsprinzip von RAM zu veranschaulichen.
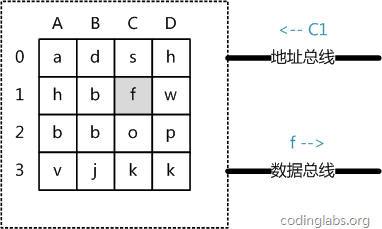
Bild 5
Aus abstrakter Sicht ist der Hauptspeicher eine Matrix, die aus einer Reihe von Speichereinheiten besteht, wobei jede Speichereinheit Daten fester Größe speichert. Jede Speichereinheit hat eine eindeutige Adresse. Die Adressierungsregeln moderner Hauptspeicher sind hier vereinfacht auf eine zweidimensionale Adresse beschränkt: Eine Speichereinheit kann durch eine Zeilenadresse und eine Spaltenadresse eindeutig lokalisiert werden. Abbildung 5 zeigt ein 4 x 4 Hauptspeichermodell.
Der Hauptspeicherzugriffsprozess ist wie folgt:
Wenn das System den Hauptspeicher lesen muss, wird das Adresssignal auf den Adressbus gelegt und nach dem Hauptspeicher an den Hauptspeicher weitergeleitet Der Speicher liest das Adresssignal, analysiert das Signal, lokalisiert die angegebene Speichereinheit und stellt dann die Daten dieser Speichereinheit auf den Datenbus, damit andere Komponenten sie lesen können.
Der Vorgang des Schreibens in den Hauptspeicher ist ähnlich. Das System platziert die Geräteadresse und die zu schreibenden Daten auf dem Adressbus bzw. dem Datenbus. Der Hauptspeicher liest den Inhalt der beiden Busse und führt den entsprechenden Schreibvorgang durch Operationen.
Hier ist zu erkennen, dass die Zeit des Hauptspeicherzugriffs nur linear mit der Anzahl der Zugriffe zusammenhängt. Da keine mechanische Operation erfolgt, hat die „Entfernung“ der Daten, auf die zweimal zugegriffen wird, keinen Einfluss der Zeitaufwand, wenn man zuerst A0 und dann A1 nimmt, ist der gleiche wie wenn man zuerst A0 und dann D3 nimmt.
Prinzipien des Festplattenzugriffs
Wie oben erwähnt, werden Indizes im Allgemeinen in Form von Dateien auf der Festplatte gespeichert, und der Indexabruf erfordert Festplatten-E/A-Vorgänge. Im Gegensatz zum Hauptspeicher fallen bei Festplatten-I/O Kosten für die mechanische Bewegung an, sodass der Zeitaufwand für Festplatten-I/O enorm ist.
Abbildung 6 ist ein schematisches Diagramm der Gesamtstruktur der Festplatte.
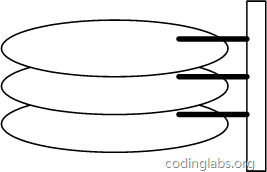
Abbildung 6
Eine Scheibe besteht aus kreisförmigen Scheiben gleicher Größe und Koaxialität. Die Scheiben können rotieren (jede Scheibe muss synchron rotieren). Auf einer Seite der Festplatte befindet sich eine Kopfhalterung. Die Kopfhalterung fixiert einen Satz Köpfe. Jeder Kopf ist für den Zugriff auf den Inhalt einer Festplatte verantwortlich. Der Magnetkopf kann sich nicht drehen, aber er kann sich entlang des Radius der Platte bewegen (eigentlich schräge tangentiale Bewegung). Jeder Magnetkopf muss gleichzeitig koaxial sein, das heißt, von direkt oben gesehen überlappen sich alle Magnetköpfe jederzeit Zeit (aber derzeit gibt es eine Multi-Head-Independent-Technologie, die dieser Einschränkung nicht unterliegt).
Abbildung 7 ist ein schematisches Diagramm der Festplattenstruktur.
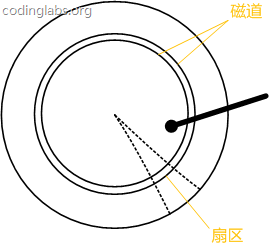
Abbildung 7
Die Scheibe ist in eine Reihe konzentrischer Ringe unterteilt, der Mittelpunkt des Kreises ist der Mittelpunkt der Scheibe, jeder konzentrische Ring ist eine Spur genannt, alle mit dem gleichen Radius. Die Spuren bilden einen Zylinder. Die Spur ist entlang der Radiuslinie in kleine Segmente unterteilt. Jedes Segment wird als Sektor bezeichnet und jeder Sektor ist die kleinste Speichereinheit der Festplatte. Der Einfachheit halber gehen wir im Folgenden davon aus, dass die Platte nur einen Plattenteller und einen Kopf hat.
Wenn Daten von der Festplatte gelesen werden müssen, überträgt das System die logische Adresse der Daten auf die Festplatte. Die Steuerschaltung der Festplatte übersetzt die logische Adresse entsprechend der Adressierungslogik in eine physische Adresse , das heißt, bestimmen Sie, auf welcher Spur sich die zu lesenden Daten befinden, in welchem Sektor. Um die Daten in diesem Sektor zu lesen, muss der Magnetkopf über diesem Sektor platziert werden. Dazu muss sich der Magnetkopf bewegen, um ihn an der entsprechenden Spur auszurichten. Dieser Vorgang wird als Suchen bezeichnet wird als Suchzeit bezeichnet. Der Zielsektor wird unter dem Kopf gedreht. Die für diesen Vorgang aufgewendete Zeit wird als Rotationszeit bezeichnet.
Lokalitätsprinzip und Festplatten-Vorauslesen
Aufgrund der Eigenschaften des Speichermediums ist der Festplattenzugriff viel langsamer als der Hauptspeicher. In Verbindung mit den Kosten für die mechanische Bewegung ist die Festplattenzugriffsgeschwindigkeit höher oft ein Hundertstel des Hauptspeichers. Um die Effizienz zu verbessern, sollte die Festplatten-E/A minimiert werden. Um dieses Ziel zu erreichen, liest die Festplatte häufig nicht ausschließlich bei Bedarf, sondern jedes Mal im Voraus. Auch wenn nur ein Byte benötigt wird, beginnt die Festplatte an dieser Position und liest sequentiell eine bestimmte Länge an Daten rückwärts Erinnerung. Die theoretische Grundlage dafür ist das berühmte Lokalitätsprinzip der Informatik:
Wenn ein Datenelement verwendet wird, werden die Daten in der Nähe normalerweise sofort verwendet.
Die während der Programmausführung erforderlichen Daten sind normalerweise konzentriert.
Da sequentielle Lesevorgänge auf der Festplatte sehr effizient sind (keine Suchzeit erforderlich, sehr kurze Spin-Zeit), kann das Vorauslesen die E/A-Effizienz für Programme mit Lokalität verbessern.
Die Read-Ahead-Länge ist im Allgemeinen ein ganzzahliges Vielfaches der Seite. Seiten sind logische Blöcke des vom Computer verwalteten Speichers. Hardware und Betriebssysteme unterteilen häufig Hauptspeicher- und Festplattenspeicherbereiche in aufeinanderfolgende gleich große Blöcke. Jeder Speicherblock wird als Seite bezeichnet (in vielen Betriebssystemen beträgt die Seitengröße normalerweise 4 KB). Hauptspeicher und Festplattenaustauschdaten in Seiteneinheiten. Wenn sich die vom Programm zu lesenden Daten nicht im Hauptspeicher befinden, wird eine Seitenfehlerausnahme ausgelöst. Zu diesem Zeitpunkt sendet das System ein Lesesignal an die Festplatte und die Festplatte findet die Startposition der Daten und eine oder mehrere Seiten rückwärts lesen, dann abnormal zurückkehren und das Programm weiter ausführen.
Leistungsanalyse des B-/+Tree-Index
An diesem Punkt können wir endlich die Leistung des B-/+Tree-Index analysieren.
Wie oben erwähnt, werden Festplatten-E/A-Zeiten im Allgemeinen verwendet, um die Qualität der Indexstruktur zu bewerten. Beginnen wir mit der B-Tree-Analyse. Gemäß der Definition von B-Tree ist ersichtlich, dass für einen Abruf maximal h Knoten besucht werden müssen. Die Designer des Datenbanksystems machten sich geschickt das Disk-Read-Ahead-Prinzip zunutze und legten die Größe eines Knotens auf eine Seite fest, sodass jeder Knoten mit nur einem I/O vollständig geladen werden kann. Um dieses Ziel zu erreichen, müssen bei der tatsächlichen Implementierung von B-Tree die folgenden Techniken verwendet werden:
Beantragen Sie bei jeder Erstellung eines neuen Knotens direkt eine Seite mit Speicherplatz, um sicherzustellen, dass ein Knoten vorhanden ist wird physisch auf einer Seite gespeichert. Darüber hinaus ist die Speicherzuweisung des Computers seitenorientiert, was bedeutet, dass für einen Knoten nur eine E/A erforderlich ist.
Ein Abruf im B-Tree erfordert höchstens h-1 I/O (Wurzelknoten-residenter Speicher) und die asymptotische Komplexität ist O(h)=O(logdN). In allgemeinen praktischen Anwendungen ist der Out-Grad d eine sehr große Zahl, normalerweise mehr als 100, sodass h sehr klein ist (normalerweise nicht mehr als 3).
Zusammenfassend ist die Verwendung von B-Tree als Indexstruktur sehr effizient.
Was die rot-schwarze Baumstruktur betrifft, ist h offensichtlich viel tiefer. Da logisch nahe Knoten (Eltern und Kinder) physisch weit entfernt sein können, kann die Lokalität nicht ausgenutzt werden, sodass die asymptotische E/A-Komplexität des rot-schwarzen Baums ebenfalls O (h) ist und die Effizienz offensichtlich viel schlechter ist als die von der B-Baum.
Wie oben erwähnt, eignet sich B+Tree besser für externe Speicherindizes. Der Grund liegt im Out-Grade d des internen Knotens. Aus der obigen Analyse können wir ersehen, dass die Leistung des Index umso besser ist, je größer d ist. Die Obergrenze des Out-Grades hängt von der Größe des Schlüssels und der Daten im Knoten ab:
dmax = floor(pagesize / (keysize + datasize + pointsize) ) (pagesize – dmax >= pointsize)
oder
dmax = floor(pagesize / (keysize + datasize + pointsize)) – 1 (Seitengröße – dmax < Punktgröße)
Untergrenze bedeutet Abrunden. Da die Datendomäne von den Knoten in B+Tree entfernt wird, können sie größere Out-Grade und eine bessere Leistung haben.
In diesem Kapitel werden die Datenstruktur- und Algorithmusprobleme im Zusammenhang mit Indizes aus theoretischer Sicht erörtert. Im nächsten Kapitel wird erläutert, wie B+Tree speziell als Index in MySQL implementiert wird, und es werden auch die Speicher MyISAM und InnDB vorgestellt Es gibt zwei verschiedene Formen der Indeximplementierung: Nicht-Clustered-Index und Clustered-Index.
MySQL-Indeximplementierung
Indizes sind Konzepte auf Speicher-Engine-Ebene. In diesem Artikel werden hauptsächlich die beiden Speicher-Engines MyISAM und InnoDB-Indeximplementierung beschrieben.
MyISAM-Indeximplementierung
Die MyISAM-Engine verwendet B+Tree als Indexstruktur und das Datenfeld des Blattknotens speichert die Adresse des Datensatzes. Die folgende Abbildung ist das schematische Diagramm des MyISAM-Index:
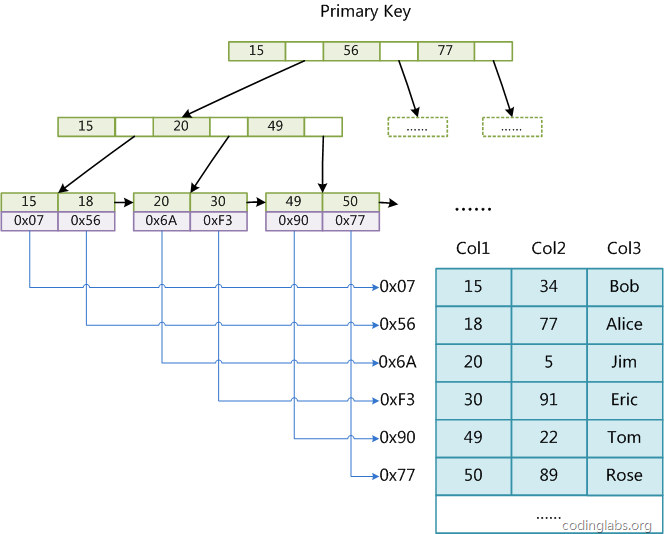
Abbildung 8
Die Tabelle hier hat insgesamt drei Spalten als Primärschlüssel, dann Abbildung 8 Es ist die primäre Indexdarstellung (Primärschlüssel) einer MyISAM-Tabelle. Es ist ersichtlich, dass die Indexdatei von MyISAM nur die Adresse des Datensatzes speichert. In MyISAM gibt es keinen strukturellen Unterschied zwischen dem Primärindex und dem Sekundärindex (Sekundärschlüssel), außer dass der Primärindex einen eindeutigen Schlüssel erfordert, während der Schlüssel des Sekundärindex wiederholt werden kann. Wenn wir einen Hilfsindex für Col2 erstellen, sieht die Struktur dieses Index wie folgt aus:
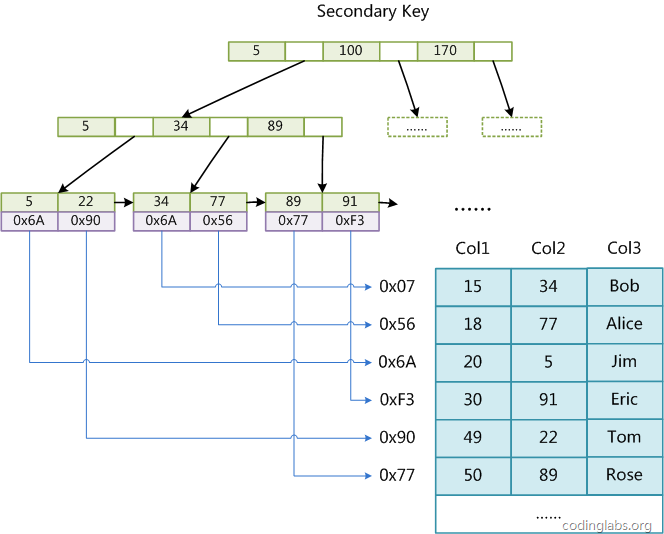
Abbildung 9
ist auch ein B+Baum Das Datenfeld speichert die Adresse des Datensatzes. Daher besteht der Indexabrufalgorithmus in MyISAM darin, zuerst den Index gemäß dem B+Tree-Suchalgorithmus zu durchsuchen. Wenn der angegebene Schlüssel vorhanden ist, wird der Wert seines Datenfelds entnommen und dann der Wert des Datenfelds verwendet die Adresse zum Lesen des entsprechenden Datensatzes.
Die Indexierungsmethode von MyISAM wird auch „nicht geclustert“ genannt. Der Grund, warum sie so genannt wird, besteht darin, sie vom Clustered-Index von InnoDB zu unterscheiden.
InnoDB-Indeximplementierung
Obwohl InnoDB auch B+Tree als Indexstruktur verwendet, unterscheidet sich die spezifische Implementierungsmethode völlig von MyISAM.
Der erste große Unterschied besteht darin, dass die Datendateien von InnoDB selbst Indexdateien sind. Wie wir aus dem Obigen wissen, sind die MyISAM-Indexdatei und die Datendatei getrennt und die Indexdatei speichert nur die Adresse des Datensatzes. In InnoDB ist die Tabellendatendatei selbst eine von B + Tree organisierte Indexstruktur, und das Blattknoten-Datenfeld dieses Baums speichert vollständige Datensätze. Der Schlüssel dieses Index ist der Primärschlüssel der Datentabelle, daher ist die InnoDB-Tabellendatendatei selbst der Primärindex.
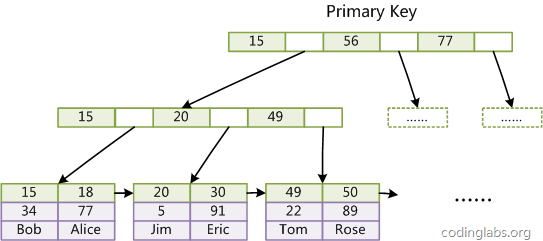
Bild 10
图10是InnoDB主索引(同时也是数据文件)的示意图,可以看到叶节点包含了完整的数据记录。这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键(MyISAM可以没有),如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
第二个与MyISAM索引的不同是InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说,InnoDB的所有辅助索引都引用主键作为data域。例如,图11为定义在Col3上的一个辅助索引:
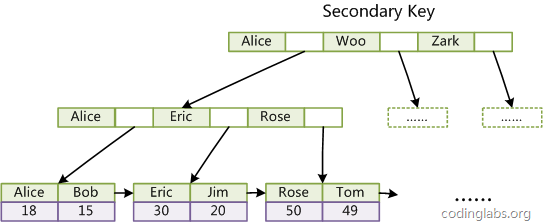
图11
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效,但是辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
了解不同存储引擎的索引实现方式对于正确使用和优化索引都非常有帮助,例如知道了InnoDB的索引实现后,就很容易明白为什么不建议使用过长的字段作为主键,因为所有辅助索引都引用主索引,过长的主索引会令辅助索引变得过大。再例如,用非单调的字段作为主键在InnoDB中不是个好主意,因为InnoDB数据文件本身是一颗B+Tree,非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整,十分低效,而使用自增字段作为主键则是一个很好的选择。
下一章将具体讨论这些与索引有关的优化策略。
索引使用策略及优化
MySQL的优化主要分为结构优化(Scheme optimization)和查询优化(Query optimization)。本章讨论的高性能索引策略主要属于结构优化范畴。本章的内容完全基于上文的理论基础,实际上一旦理解了索引背后的机制,那么选择高性能的策略就变成了纯粹的推理,并且可以理解这些策略背后的逻辑。
示例数据库
为了讨论索引策略,需要一个数据量不算小的数据库作为示例。本文选用MySQL官方文档中提供的示例数据库之一:employees。这个数据库关系复杂度适中,且数据量较大。下图是这个数据库的E-R关系图(引用自MySQL官方手册):
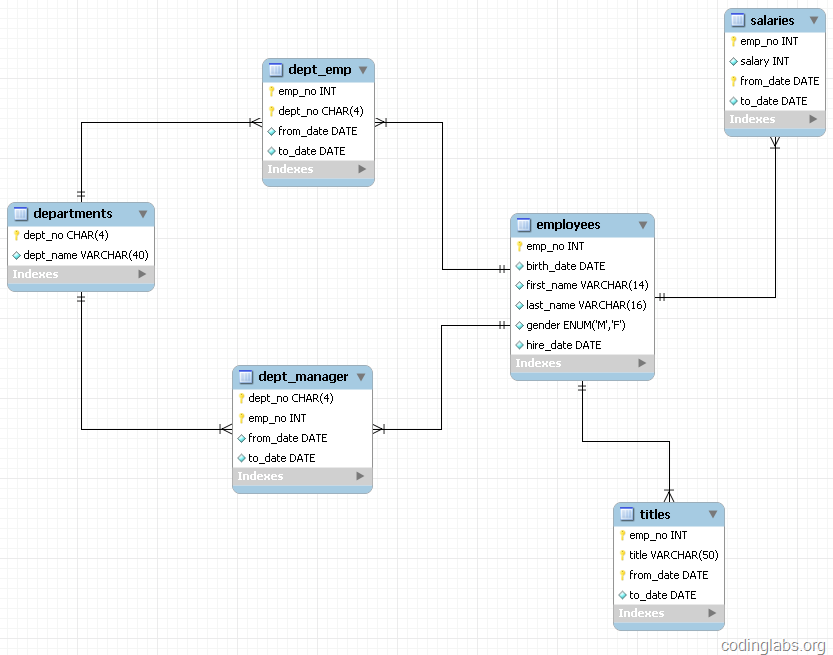
图12
MySQL官方文档中关于此数据库的页面为http://dev.mysql.com/doc/employee/en/employee.html。里面详细介绍了此数据库,并提供了下载地址和导入方法,如果有兴趣导入此数据库到自己的MySQL可以参考文中内容。
最左前缀原理与相关优化
高效使用索引的首要条件是知道什么样的查询会使用到索引,这个问题和B+Tree中的“最左前缀原理”有关,下面通过例子说明最左前缀原理。
这里先说一下联合索引的概念。在上文中,我们都是假设索引只引用了单个的列,实际上,MySQL中的索引可以以一定顺序引用多个列,这种索引叫做联合索引,一般的,一个联合索引是一个有序元组
以employees.titles表为例,下面先查看其上都有哪些索引:
SHOW INDEX FROM employees.titles; +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | Table | Non_unique | Key_name | Seq_in_index | Column_name | Collation | Cardinality | Null | Index_type | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | titles | 0 | PRIMARY | 1 | emp_no | A | NULL | | BTREE | | titles | 0 | PRIMARY | 2 | title | A | NULL | | BTREE | | titles | 0 | PRIMARY | 3 | from_date | A | 443308 | | BTREE | | titles | 1 | emp_no | 1 | emp_no | A | 443308 | | BTREE | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+
从结果中可以到titles表的主索引为
ALTER TABLE employees.titles DROP INDEX emp_no;
这样就可以专心分析索引PRIMARY的行为了。
情况一:全列匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title='Senior Engineer' AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
很明显,当按照索引中所有列进行精确匹配(这里精确匹配指“=”或“IN”匹配)时,索引可以被用到。这里有一点需要注意,理论上索引对顺序是敏感的,但是由于MySQL的查询优化器会自动调整where子句的条件顺序以使用适合的索引,例如我们将where中的条件顺序颠倒:
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26' AND emp_no='10001' AND title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
效果是一样的。
情况二:最左前缀匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+
当查询条件精确匹配索引的左边连续一个或几个列时,如
情况三:查询条件用到了索引中列的精确匹配,但是中间某个条件未提供。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
此时索引使用情况和情况二相同,因为title未提供,所以查询只用到了索引的第一列,而后面的from_date虽然也在索引中,但是由于title不存在而无法和左前缀连接,因此需要对结果进行扫描过滤from_date(这里由于emp_no唯一,所以不存在扫描)。如果想让from_date也使用索引而不是where过滤,可以增加一个辅助索引
首先我们看下title一共有几种不同的值:
SELECT DISTINCT(title) FROM employees.titles; +--------------------+ | title | +--------------------+ | Senior Engineer | | Staff | | Engineer | | Senior Staff | | Assistant Engineer | | Technique Leader | | Manager | +--------------------+
只有7种。在这种成为“坑”的列值比较少的情况下,可以考虑用“IN”来填补这个“坑”从而形成最左前缀:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ('Senior Engineer', 'Staff', 'Engineer', 'Senior Staff', 'Assistant Engineer', 'Technique Leader', 'Manager') AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 7 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
这次key_len为59,说明索引被用全了,但是从type和rows看出IN实际上执行了一个range查询,这里检查了7个key。看下两种查询的性能比较:
SHOW PROFILES; +----------+------------+-------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+-------------------------------------------------------------------------------+ | 10 | 0.00058000 | SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'| | 11 | 0.00052500 | SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ... | +----------+------------+-------------------------------------------------------------------------------+
“填坑”后性能提升了一点。如果经过emp_no筛选后余下很多数据,则后者性能优势会更加明显。当然,如果title的值很多,用填坑就不合适了,必须建立辅助索引。
情况四:查询条件没有指定索引第一列。
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
由于不是最左前缀,索引这样的查询显然用不到索引。
情况五:匹配某列的前缀字符串。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title LIKE 'Senior%'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 56 | NULL | 1 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
此时可以用到索引,但是如果通配符不是只出现在末尾,则无法使用索引。(原文表述有误,如果通配符%不出现在开头,则可以用到索引,但根据具体情况不同可能只会用其中一个前缀)
情况六:范围查询。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < '10010' and title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
范围列可以用到索引(必须是最左前缀),但是范围列后面的列无法用到索引。同时,索引最多用于一个范围列,因此如果查询条件中有两个范围列则无法全用到索引。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < 10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
可以看到索引对第二个范围索引无能为力。这里特别要说明MySQL一个有意思的地方,那就是仅用explain可能无法区分范围索引和多值匹配,因为在type中这两者都显示为range。同时,用了“between”并不意味着就是范围查询,例如下面的查询:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no BETWEEN '10001' AND '10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
看起来是用了两个范围查询,但作用于emp_no上的“BETWEEN”实际上相当于“IN”,也就是说emp_no实际是多值精确匹配。可以看到这个查询用到了索引全部三个列。因此在MySQL中要谨慎地区分多值匹配和范围匹配,否则会对MySQL的行为产生困惑。
情况七:查询条件中含有函数或表达式。
很不幸,如果查询条件中含有函数或表达式,则MySQL不会为这列使用索引(虽然某些在数学意义上可以使用)。例如:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND left(title, 6)='Senior'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
虽然这个查询和情况五中功能相同,但是由于使用了函数left,则无法为title列应用索引,而情况五中用LIKE则可以。再如:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no - 1='10000'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
显然这个查询等价于查询emp_no为10001的函数,但是由于查询条件是一个表达式,MySQL无法为其使用索引。看来MySQL还没有智能到自动优化常量表达式的程度,因此在写查询语句时尽量避免表达式出现在查询中,而是先手工私下代数运算,转换为无表达式的查询语句。
索引选择性与前缀索引
既然索引可以加快查询速度,那么是不是只要是查询语句需要,就建上索引?答案是否定的。因为索引虽然加快了查询速度,但索引也是有代价的:索引文件本身要消耗存储空间,同时索引会加重插入、删除和修改记录时的负担,另外,MySQL在运行时也要消耗资源维护索引,因此索引并不是越多越好。一般两种情况下不建议建索引。
第一种情况是表记录比较少,例如一两千条甚至只有几百条记录的表,没必要建索引,让查询做全表扫描就好了。至于多少条记录才算多,这个个人有个人的看法,我个人的经验是以2000作为分界线,记录数不超过 2000可以考虑不建索引,超过2000条可以酌情考虑索引。
另一种不建议建索引的情况是索引的选择性较低。所谓索引的选择性(Selectivity),是指不重复的索引值(也叫基数,Cardinality)与表记录数(#T)的比值:
Index Selectivity = Cardinality / #T
显然选择性的取值范围为(0, 1],选择性越高的索引价值越大,这是由B+Tree的性质决定的。例如,上文用到的employees.titles表,如果title字段经常被单独查询,是否需要建索引,我们看一下它的选择性:
SELECT count(DISTINCT(title))/count(*) AS Selectivity FROM employees.titles; +-------------+ | Selectivity | +-------------+ | 0.0000 | +-------------+
title的选择性不足0.0001(精确值为0.00001579),所以实在没有什么必要为其单独建索引。
有一种与索引选择性有关的索引优化策略叫做前缀索引,就是用列的前缀代替整个列作为索引key,当前缀长度合适时,可以做到既使得前缀索引的选择性接近全列索引,同时因为索引key变短而减少了索引文件的大小和维护开销。下面以employees.employees表为例介绍前缀索引的选择和使用。
从图12可以看到employees表只有一个索引
EXPLAIN SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido'; +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | employees | ALL | NULL | NULL | NULL | NULL | 300024 | Using where | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+
如果频繁按名字搜索员工,这样显然效率很低,因此我们可以考虑建索引。有两种选择,建
SELECT count(DISTINCT(first_name))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.0042 | +-------------+ SELECT count(DISTINCT(concat(first_name, last_name)))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9313 | +-------------+
SELECT count(DISTINCT(concat(first_name, left(last_name, 3))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.7879 | +-------------+
选择性还不错,但离0.9313还是有点距离,那么把last_name前缀加到4:
SELECT count(DISTINCT(concat(first_name, left(last_name, 4))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9007 | +-------------+
这时选择性已经很理想了,而这个索引的长度只有18,比
ALTER TABLE employees.employees ADD INDEX `first_name_last_name4` (first_name, last_name(4));
此时再执行一遍按名字查询,比较分析一下与建索引前的结果:
SHOW PROFILES; +----------+------------+---------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+---------------------------------------------------------------------------------+ | 87 | 0.11941700 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | | 90 | 0.00092400 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | +----------+------------+---------------------------------------------------------------------------------+
性能的提升是显著的,查询速度提高了120多倍。
前缀索引兼顾索引大小和查询速度,但是其缺点是不能用于ORDER BY和GROUP BY操作,也不能用于Covering index(即当索引本身包含查询所需全部数据时,不再访问数据文件本身)。
InnoDB的主键选择与插入优化
在使用InnoDB存储引擎时,如果没有特别的需要,请永远使用一个与业务无关的自增字段作为主键。
经常看到有帖子或博客讨论主键选择问题,有人建议使用业务无关的自增主键,有人觉得没有必要,完全可以使用如学号或身份证号这种唯一字段作为主键。不论支持哪种论点,大多数论据都是业务层面的。如果从数据库索引优化角度看,使用InnoDB引擎而不使用自增主键绝对是一个糟糕的主意。
上文讨论过InnoDB的索引实现,InnoDB使用聚集索引,数据记录本身被存于主索引(一颗B+Tree)的叶子节点上。这就要求同一个叶子节点内(大小为一个内存页或磁盘页)的各条数据记录按主键顺序存放,因此每当有一条新的记录插入时,MySQL会根据其主键将其插入适当的节点和位置,如果页面达到装载因子(InnoDB默认为15/16),则开辟一个新的页(节点)。
如果表使用自增主键,那么每次插入新的记录,记录就会顺序添加到当前索引节点的后续位置,当一页写满,就会自动开辟一个新的页。如下图所示:
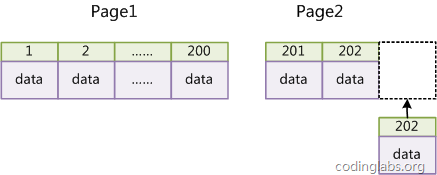
图13
这样就会形成一个紧凑的索引结构,近似顺序填满。由于每次插入时也不需要移动已有数据,因此效率很高,也不会增加很多开销在维护索引上。
如果使用非自增主键(如果身份证号或学号等),由于每次插入主键的值近似于随机,因此每次新纪录都要被插到现有索引页得中间某个位置:
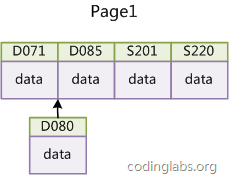
图14
此时MySQL不得不为了将新记录插到合适位置而移动数据,甚至目标页面可能已经被回写到磁盘上而从缓存中清掉,此时又要从磁盘上读回来,这增加了很多开销,同时频繁的移动、分页操作造成了大量的碎片,得到了不够紧凑的索引结构,后续不得不通过OPTIMIZE TABLE来重建表并优化填充页面。
因此,只要可以,请尽量在InnoDB上采用自增字段做主键。
后记
Ich schreibe diesen Artikel seit einem halben Monat hin und wieder und der Hauptinhalt ist der oben genannte. Es lässt sich nicht leugnen, dass es sich bei diesem Artikel bis zu einem gewissen Grad um eine Art Sesselübung handelt, da ich mich mit MySQL noch auf Anfängerniveau befinde und nicht viel Erfahrung mit der Optimierung von Datenbanken habe. Es wäre etwas anmaßend, darüber zu sprechen Optimierung des Datenbankindex finden Sie hier. Behandeln Sie es einfach als meine persönlichen Studiennotizen.
Tatsächlich ist die Optimierung des Datenbankindex eine technische Aktivität und kann sich nicht nur auf die Theorie verlassen, da sich die tatsächliche Situation ständig ändert und MySQL selbst über sehr komplexe Mechanismen verfügt, wie z. B. Strategien zur Abfrageoptimierung und Implementierungsunterschiede verschiedener Motoren. Die Situation wird komplizierter. Aber gleichzeitig sind diese Theorien die Grundlage für die Indexoptimierung. Nur wenn wir die Theorie verstehen, können wir vernünftige Rückschlüsse auf die Optimierungsstrategie ziehen und den dahinter stehenden Mechanismus verstehen Erreichen Sie eine effiziente Nutzung von MySQL.
Darüber hinaus decken MySQL-Indizes und ihre Optimierung ein sehr breites Spektrum ab, und dieser Artikel berührt nur einen Teil davon. Beispielsweise werden die Themen Indexoptimierung und Index im Zusammenhang mit der Sortierung (ORDER BY) in diesem Artikel nicht behandelt. Zusätzlich zum B-Tree-Index unterstützt MySQL auch Hash-Indizes, Volltextindizes usw. basierend auf verschiedenen Engines . Dieser Artikel deckt auch nicht ab. Wenn Sie die Möglichkeit haben, hoffe ich, einige Teile hinzuzufügen, die in diesem Artikel nicht behandelt werden.
Referenzen
[1] Baron Scbwartz et al. Übersetzt von Wang Xiaodong et al.; High Performance MySQL; 2010
[2] Geschrieben von Michael Kofler, übersetzt von Yang Xiaoyun und anderen; The Definitive Guide to MySQL5; People's Posts and Telecommunications Publishing House, 2006
[3] Verfasst von Jiang Chengyao; MySQL Technology Insider-InnoDB Storage Engine, 2011
[4] D Comer, Ubiquitous B-tree; ACM Computing Surveys (CSUR), 1979
[5] Codd, E. F. (1970). Datenbanken". Communications of the ACM, , Band 13, Nr. 6, S. 377-387
[6] MySQL5.1 Referenzhandbuch – http://dev.mysql.com/doc / refman/5.1/zh/index.html
Ausführlichere Erläuterungen zur Datenstruktur und den Algorithmusprinzipien hinter MySQL-Indizes finden Sie auf der chinesischen PHP-Website!
 Wie man unter Linux mit verstümmelten chinesischen Schriftzeichen umgeht
Wie man unter Linux mit verstümmelten chinesischen Schriftzeichen umgeht
 Die Rolle des Routers
Die Rolle des Routers
 Die Rolle des Formatfactory-Tools
Die Rolle des Formatfactory-Tools
 NumberFormatException
NumberFormatException
 So ändern Sie die Hintergrundfarbe eines Wortes in Weiß
So ändern Sie die Hintergrundfarbe eines Wortes in Weiß
 Wörter verschwinden nach dem Tippen
Wörter verschwinden nach dem Tippen
 Lösung für die Erlaubnis verweigert
Lösung für die Erlaubnis verweigert
 Eigenschaften relationaler Datenbanken
Eigenschaften relationaler Datenbanken




