Analyse des Implementierungsprinzips von Java8 HashMap-javaLernprogramm-php.cn

Die Speicherstruktur von HashMap ist wie in der Abbildung dargestellt: Wenn ein Bucket mehr als 8 Knoten enthält, ist die Speicherstruktur ein rot-schwarzer Baum, und wenn weniger als 8 Knoten vorhanden sind, handelt es sich um einen Ein- Art und Weise verknüpfte Liste.

Java8 HashMap的实现原理分析

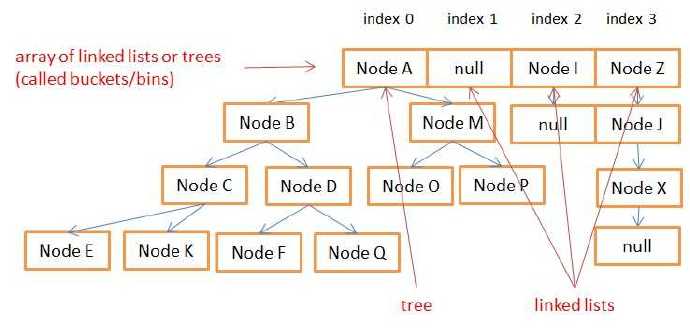
1: Einige Eigenschaften von HashMap

public class HashMap<k,v> extends AbstractMap<k,v> implements Map<k,v>, Cloneable, Serializable {
private static final long serialVersionUID = 362498820763181265L;
// 默认的初始容量是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
// 默认的填充因子(以前的版本也有叫加载因子的)
static final float DEFAULT_LOAD_FACTOR = 0.75f;
// 这是一个阈值，当桶(bucket)上的链表数大于这个值时会转成红黑树，put方法的代码里有用到
static final int TREEIFY_THRESHOLD = 8;
// 也是阈值同上一个相反，当桶(bucket)上的链表数小于这个值时树转链表
static final int UNTREEIFY_THRESHOLD = 6;
// 看源码注释里说是：树的最小的容量，至少是 4 x TREEIFY_THRESHOLD = 32 然后为了避免(resizing 和 treeification thresholds) 设置成64
static final int MIN_TREEIFY_CAPACITY = 64;
// 存储元素的数组，总是2的倍数
transient Node<k,v>[] table;
transient Set<map.entry<k,v>> entrySet;
// 存放元素的个数，注意这个不等于数组的长度。
transient int size;
// 每次扩容和更改map结构的计数器
transient int modCount;
// 临界值 当实际大小(容量*填充因子)超过临界值时，会进行扩容
int threshold;
// 填充因子
final float loadFactor;

Nach dem Login kopieren

2: Konstruktionsmethode von HashMap

// 指定初始容量和填充因子的构造方法
public HashMap(int initialCapacity, float loadFactor) {
// 指定的初始容量非负
if (initialCapacity < 0)
throw new IllegalArgumentException(Illegal initial capacity: +
initialCapacity);
// 如果指定的初始容量大于最大容量,置为最大容量
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// 填充比为正
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException(Illegal load factor: +
loadFactor);
this.loadFactor = loadFactor;
// 指定容量后，tableSizeFor方法计算出临界值，put数据的时候如果超出该值就会扩容，该值肯定也是2的倍数
// 指定的初始容量没有保存下来，只用来生成了一个临界值
this.threshold = tableSizeFor(initialCapacity);
}
// 该方法保证总是返回大于cap并且是2的倍数的值，比如传入999 返回1024
static final int tableSizeFor(int cap) {
int n = cap - 1;
// 向右做无符号位移
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
// 三目运算符的嵌套
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
//构造函数2
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//构造函数3
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

Nach dem Login kopieren

3: Bestimmen Sie die Position des Elements im Array beim Abrufen und Einfügen von

static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Nach dem Login kopieren

Um den Standort zu bestimmen

Der erste Schritt besteht darin, den Hash-Code des Schlüssels zu berechnen, bei dem es sich um eine Zahl vom Typ int handelt. Die folgenden h >>> 16 Quellcode-Kommentare besagen: Um Hash-Kollisionen (Hash-Kollisonen) zu vermeiden, werden die hohen Bits auf die niedrigen Bits verteilt. Dies erfolgt nach umfassender Berücksichtigung verschiedener Faktoren wie Geschwindigkeit und Leistung .

Schritt 2: h ist der Hash-Code, Länge ist die Länge des Node[]-Arrays oben, führen Sie die UND-Operation h & (Länge-1) aus. Da die Länge ein Vielfaches von 2 -1 ist, ist ihr Binärcode alle 1, und das Ergebnis von 1 und anderen oben genannten Zahlen kann 0 oder 1 sein, wodurch die Einheitlichkeit nach der Operation gewährleistet wird. Das heißt, die Hash-Methode stellt die Einheitlichkeit der Ergebnisse sicher, was sehr wichtig ist und einen großen Einfluss auf die Put- und Get-Leistung von HashMap hat. Schauen Sie sich den Vergleich unten an:

Java8 HashMap的实现原理分析

Abbildung 3.1 ist das asymmetrische Hash-Ergebnis

Java8 HashMap的实现原理分析

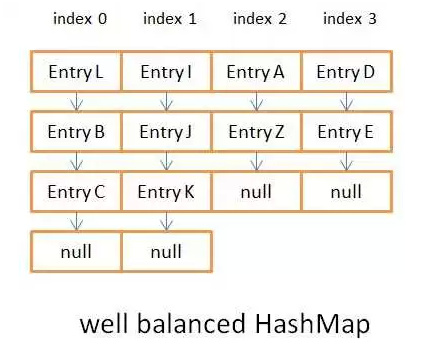
Abbildung 3.2 ist das ausgeglichene Hash-Ergebnis

Diese beiden Bilder enthalten nicht viele Daten. Wenn die Länge der verknüpften Liste 8 überschreitet, wird sie in einen rot-schwarzen Baum umgewandelt. Zu diesem Zeitpunkt wird es offensichtlicher sein, dass es sich immer um eine verknüpfte Liste handelt. Die Komplexität der Abfrage einer verknüpften Liste beträgt O (n), während die Abfragekomplexität des Rot-Schwarz-Baums O (log (n)) beträgt zu seinen eigenen Eigenschaften. Wenn die Hash-Ergebnisse ungleichmäßig sind, wirkt sich dies stark auf die Komplexität des Vorgangs aus. Verwandtes Wissen finden Sie hierRed-Black Tree Basic Knowledge BlogEs gibt auch ein Beispiel im Internet Zur Überprüfung: Passen Sie ein Objekt als Schlüssel an, passen Sie die Methode hashCode() an, um zu sehen, wie lange es dauert,

public class MutableKeyTest {
public static void main(String args[]){
class MyKey {
Integer i;
public void setI(Integer i) {
this.i = i;
}
public MyKey(Integer i) {
this.i = i;
}
@Override
public int hashCode() {
// 如果返回1
// return 1
return i;
}
// object作为key存map里，必须实现equals方法
@Override
public boolean equals(Object obj) {
if (obj instanceof MyKey) {
return i.equals(((MyKey)obj).i);
} else {
return false;
}
}
}
// 我机器配置不高，25000的话正常情况27毫秒，可以用2500万试试，如果hashCode()方法返回1的话，250万就卡死
Map<MyKey,String> map = new HashMap<>(25000,1);
Date begin = new Date();
for (int i = 0; i < 20000; i++){
map.put(new MyKey(i), "test " + i);
}
Date end = new Date();
System.out.println("时间(ms) " + (end.getTime() - begin.getTime()));

Nach dem Login kopieren

4: get method < einzufügen 🎜>

public V get(Object key) {
Node<k,v> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<k,v> getNode(int hash, Object key) {
Node<k,v>[] tab; Node<k,v> first, e; int n; K k;
// hash & (length-1)得到红黑树的树根位置或者是链表的表头
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// 如果是树，遍历红黑树复杂度是O(log(n))，得到节点值
if (first instanceof TreeNode)
return ((TreeNode<k,v>)first).getTreeNode(hash, key);
// else是链表结构
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}

Nach dem Login kopieren

5: Put-Methode: Suchen Sie beim Putten den Eimer nach h & (Länge – 1) und prüfen Sie dann, ob es sich um einen Rot-Schwarzen handelt Baum oder eine verknüpfte Liste und dann putVal

public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<k,v>[] tab; Node<k,v> p; int n, i;
// 如果tab为空或长度为0，则分配内存resize()
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n - 1) & hash找到put位置，如果为空,则直接put
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<k,v> e; K k;
// 第一节节点hash值同，且key值与插入key相同
if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
// 红黑树的put方法比较复杂，putVal之后还要遍历整个树，必要的时候修改值来保证红黑树的特点
e = ((TreeNode<k,v>)p).putTreeVal(this, tab, hash, key, value);
else {
// 链表
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
// e为空，表示已到表尾也没有找到key值相同节点，则新建节点
p.next = newNode(hash, key, value, null);
// 新增节点后如果节点个数到达阈值，则将链表转换为红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 容许空key空value
if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 更新hash值和key值均相同的节点Value值
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}

Nach dem Login kopieren

6: Größenänderungsmethode

final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 这一句比较重要，可以看出每次扩容是2倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}

Nach dem Login kopieren

Das Obige ist der Herausgeber. Ich möchte Ihnen das relevante Wissen über die Analyse des Implementierungsprinzips von Java8 HashMap vorstellen. Ich hoffe, es wird Ihnen hilfreich sein!

Weitere Artikel zur Analyse der Implementierungsprinzipien von Java8 HashMap finden Sie auf der chinesischen PHP-Website!