In der unendlichen Klassifizierung von PHP sind viele Methoden rekursiv, aber unser Verständnis der Rekursion ist noch vage. Als nächstes werden wir uns eingehend mit den Vor- und Nachteilen der Rekursion befassen, damit jeder sie verstehen kann Umfassendes Verständnis.
Was ist Rekursion?
Definition
Rekursion (englisch: Recursion), in der Mathematik und Informatik auch als Rekursion übersetzt, bezieht sich auf die Funktion, die Methoden verwenden die Funktion selbst in der Definition.
Die etymologische Analyse der englischen Rekursion lautet einfach „re- (again)“ + „curs- (come, passieren)“, was immer wieder passieren bedeutet. Die entsprechende chinesische Übersetzung „Rekursion“ drückt zwei Bedeutungen aus: „Rekursion“ + „Rückkehr“. Diese beiden Bedeutungen sind die Essenz des rekursiven Denkens. Aus dieser Perspektive ist die chinesische Übersetzung ausdrucksvoller.
Ich habe diesen Vergleich immer wieder im Internet gesehen:
Angenommen, Sie sind in einem Kino und möchten wissen, in welcher Reihe Sie sitzen , aber die Person vor dir Es gibt so viele, dass du zu faul bist, sie zu zählen, also fragst du die Person in der ersten Reihe „In welcher Reihe sitzt du?“, damit nach der Person vor dir (Codename A ) Ihnen antwortet, wissen Sie, in welcher Reihe Sie sich befinden – solange Sie zur Antwort von A eins hinzufügen, um Ihre Reihe zu bestimmen. Unerwarteterweise ist A fauler als Sie und möchte nicht zählen, also fragt er auch die Person vor ihm, B: „In welcher Reihe sitzen Sie?“, damit A wissen kann, in welcher Reihe er sich befindet Verwenden Sie die gleichen Schritte wie Sie. Dann macht B dasselbe. Bis die Personengruppe nach der ersten Reihe fragte, sagte die Person in der ersten Reihe zu der Person, die die Frage gestellt hatte: „Ich bin in der ersten Reihe.“ Endlich weiß jeder, in welcher Reihe er steht. Der Unterschied zwischen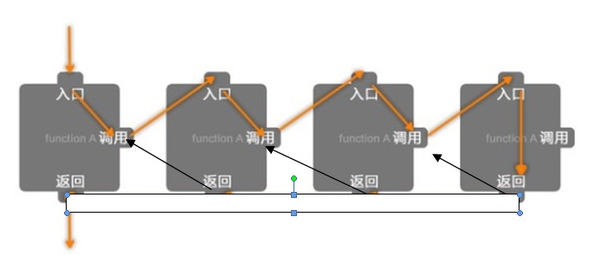 
und einer Schleife
Schauen Sie sich einfach die Definition an Aus dem Wiki oben geht hervor, dass es einer sogenannten Endlosschleife sehr ähnlich zu sein scheint. Was ist der Unterschied zwischen ihnen?
Rekursion ist Bewegung in Stille, Gehen und Zurückkehren.
Der Kreislauf ist die gleiche Bewegung und Stille, und es gibt kein Zurück.
Man bekommt zum Beispiel einen Schlüssel geschenkt. Man steht vor der Tür und fragt, wie viele Türen man mit diesem Schlüssel öffnen kann.
Rekursion: Sie öffnen die Tür vor sich und sehen eine andere Tür im Haus (diese Tür kann genauso groß sein wie die Tür, die sich vor Ihnen öffnete (ruhig), oder sie kann kleiner sein (sich bewegen)) Wenn Sie hinübergehen, stellen Sie fest, dass der Schlüssel in Ihrer Hand sie immer noch öffnen kann. Sie stoßen die Tür auf und stellen fest, dass sich darin eine weitere Tür befindet. . . , nach ein paar Malen öffnest du eine Tür vor dir und stellst fest, dass es nur einen Raum und keine Tür gibt. Sie beginnen den Rückweg auf dem gleichen Weg und zählen jedes Mal, wenn Sie in einen Raum zurückgehen, einmal. Wenn Sie den Eingang erreichen, können Sie mit diesem Schlüssel angeben, wie viele Türen Sie geöffnet haben.
Schleife: Du öffnest die Tür vor dir und siehst eine andere Tür im Haus (diese Tür kann genauso groß sein wie die Tür, die sich davor öffnete (ruhig), oder sie kann kleiner sein (sich bewegen) ), Sie gehen hinüber und stellen fest, dass der Schlüssel in Ihrer Hand sie immer noch öffnen kann. Sie stoßen die Tür auf und stellen fest, dass sich darin eine weitere Tür befindet. (Wenn die vorherige Tür dieselbe ist. Wenn die zweite Tür ist kleiner als die erste Tür, diese Tür ist auch kleiner als die zweite Tür (die Bewegung ist die gleiche, entweder keine Änderung oder die gleiche Änderung)), Sie öffnen diese Tür weiter. . . , mach weiter so. Die Person am Eingang wartet nie darauf, dass Sie zurückkommen und ihm die Antwort sagen.
Rekursives Denken
Rekursion bedeutet Gehen (Vorbeigehen) und Zurückkehren (Zurückkehren).
Warum kann man konkret „gehen“?
Das Problem, das eine Rekursion erfordert, muss in der Lage sein, dieselbe Problemlösungsidee zu verwenden, um ähnliche, aber leicht unterschiedliche Fragen zu beantworten (der Schlüssel im obigen Beispiel kann das Schloss an der Hintertür öffnen).
Warum kann ich „zurückkehren“?
Das erfordert, dass es im Prozess dieser Probleme, die sich ständig von groß nach klein, von nah nach fern bewegen, einen Endpunkt, einen kritischen Punkt, eine Grundlinie gibt, und wenn man diesen Punkt erreicht, muss man das nicht mehr tun Gehen Sie zu kleineren oder weiter entfernten Orten. Gehen Sie zum Startpunkt, starten Sie dann von diesem Punkt und kehren Sie zum ursprünglichen Punkt zurück.
Die Grundidee der Rekursion besteht darin, große Probleme in kleine, ähnliche Teilprobleme umzuwandeln, die gelöst werden müssen. Bei der Implementierung einer Funktion ruft sich die Funktion selbst auf, da die Methode zum Lösen großer Probleme und die Methode zum Lösen kleiner Probleme häufig dieselbe Methode sind. Darüber hinaus muss die Funktion, die das Problem löst, eine offensichtliche Endbedingung haben, damit keine unendliche Rekursion auftritt.
Wann müssen Sie Rekursion verwenden?
Wenn die Definition einiger Probleme selbst rekursiv ist, ist es am besten, Rekursion zu verwenden, um sie zu lösen.
Studierende im Hauptfach Informatik sind mit der Definition von „Baum“ am besten vertraut [4,5]. Es gibt auch einige Definitionen, wie zum Beispiel Fakultät, Fibonacci-Folge [6] usw. Die Verwendung von Rekursion zur Lösung dieser Probleme löst oft einige scheinbar „beängstigende“ Probleme in nur wenigen Codezeilen. Natürlich sind rekursive Leistungsprobleme eine andere Sache, die bei bestimmten Engineering-Praktiken berücksichtigt werden muss. Aber wenn wir jetzt nur rekursive Gedanken diskutieren, können wir diese genauso gut beiseite legen und die Schönheit der Rekursion schätzen.
Rekursion vereinfacht die Art und Weise, wie wir bei der Lösung bestimmter Probleme denken, und der Code ist verfeinert und leichter zu lesen. Da die Rekursion so viele Vorteile hat, sollten wir die Rekursion zur Lösung aller Probleme verwenden? Hat die Rekursion keine Nachteile? Heute werden wir die Mängel der Rekursion diskutieren. Wenn es um Rekursion geht, müssen wir uns dem Effizienzproblem stellen.
Warum ist Rekursion ineffizient?
Nehmen wir als Beispiel die Fibonacci-Folge. In vielen Lehrbüchern oder Artikeln, in denen Rekursion oder Rechenkomplexität erwähnt wird, wird das Programm zur Berechnung der Fibonacci-Folge als klassisches Beispiel verwendet. Wenn Sie nun aufgefordert werden, eine Funktion zu schreiben, die möglichst schnell die n-te Zahl der Fibonacci-Folge in C# berechnet (unabhängig von Ausnahmen wie Parameter kleiner 1 oder Ergebnisüberlauf), weiß ich nicht, ob Ihr Programm dazu passt Folgender Code ist ähnlich:
public static ulong Fib(ulong n)
{
return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}Dieser Code sollte als kurz und prägnant (nur eine Zeile Ausführungscode), intuitiv und klar angesehen werden und sehr im Einklang mit der Codeästhetik vieler Programmierer stehen Schreiben Sie solchen Code während Interviews. Vielleicht fühle ich mich insgeheim immer noch glücklich. Aber wenn Sie diesen Code verwenden, um Fib(1000) zu berechnen, werden Sie wahrscheinlich nicht mehr glücklich sein. Seine Laufzeit könnte Sie verrückt machen.
Es scheint, dass gut aussehender Code möglicherweise nicht nützlich ist. Wenn die Effizienz des Programms nicht akzeptiert werden kann, ist der gesamte gut aussehende Code umsonst. Wenn Sie den Ausführungsfluss des Programms kurz analysieren, finden Sie das Problem am Beispiel der Berechnung von Fibonacci (5):
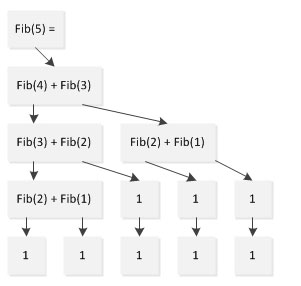
Wie aus dem ersichtlich ist Die obige Abbildung zeigt, dass bei der Berechnung von Fib im Prozess (5) Fib(1) zweimal berechnet wurde, Fib(2) dreimal berechnet wurde und Fib(3) zweimal berechnet wurde. Die Aufgabe, die ursprünglich nur 5 Berechnungen erforderte 9 Mal. Dieses Problem wird mit zunehmender Skala immer deutlicher, sodass Fib(1000) nicht mehr in akzeptabler Zeit berechnet werden kann.
Wir haben eine einfache Definition verwendet, um fib(n) zu finden, d. h. die Formel fib(n) = fib(n-1) + fib(n-2). Es ist leicht, sich diese Idee auszudenken, aber nach sorgfältiger Analyse stellen wir fest, dass beim Aufruf von fib(n-1) auch fib(n-2) aufgerufen wird, was bedeutet, dass fib(n-2) zweimal aufgerufen wird. Aus dem gleichen Grund wird f(n-3) auch zweimal aufgerufen, wenn f(n-2) aufgerufen wird, und diese redundanten Aufrufe sind völlig unnötig. Es lässt sich berechnen, dass die Komplexität dieses Algorithmus exponentiell ist.
Verbesserter rekursiver Fibonacci-Algorithmus
Gibt es also einen besseren rekursiven Algorithmus zur Berechnung der Fibonacci-Folge? Natürlich gibt es das. Werfen wir einen Blick auf die ersten paar Fibonacci-Zahlen:
11, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Haben Sie es bemerkt? Entfernen Sie den vorherigen Term, die resultierende Folge erfüllt immer noch f(n) = f(n-1) – f(n-2), (n>2), und die Folge, die wir erhalten, beginnt mit 1, 2 . Es ist leicht herauszufinden, dass das n-1-te Element dieser Sequenz das n-te Element der ursprünglichen Sequenz ist. Wie wäre es damit, wissen Sie, wie wir den Algorithmus entwerfen sollen? Wir können eine solche Funktion schreiben, die drei Parameter akzeptiert. Die ersten beiden sind die ersten beiden Elemente der Sequenz und der dritte ist die Nummer der Sequenz, die wir beginnend mit den ersten beiden Parametern finden möchten.
1int fib_i(int a, int b, int n);
Innerhalb der Funktion prüfen wir zunächst den Wert von n. Wenn n 3 ist, müssen wir nur a+b zurückgeben. Dies ist eine einfache Situation. Wenn n>3, dann rufen wir f(b, a+b, n-1) auf, was die Größe des Problems verringert (von der Suche nach dem n-ten Term zur Suche nach dem n-1-ten Term). Okay, der endgültige Code lautet wie folgt:
int fib_i(int a, int b , int n)
{
if(n == 3)
return a+b;
else
return fib_i(b, a+b, n-1);
}Warum gibt es einen großen Speicheraufwand?
Das Prinzip der Rekursion besteht darin, zuerst den zu berechnenden Variablenwert auf dem Stapel zu speichern und dann nacheinander eine Schleife auszuführen, bis die Endbedingung der Rekursion erfüllt ist. Anschließend wird der zu berechnende Variablenwert vom Stapel genommen und das Endergebnis berechnet .
Eine Analogie: Berechnen Sie 10! =
Für die Rekursion ist der Prozess: 10! =10 * 9!
9!=9 * 8!
……
2! =2*1!
1! =1
Bei der Berechnung werden Ausdrücke einzeln im Speicher gespeichert, bis die Rekursionsbedingung 1 erfüllt! =1 und rufen Sie dann den gerade gespeicherten Ausdruck aus dem Speicher ab, um das Endergebnis zu erhalten. In diesem Fall werden mehr Systemressourcen verbraucht.
Und das System legt die maximale Rekursionstiefe fest. Wenn sie größer als diese Tiefe ist, wird ein Fehler gemeldet und beendet. Beim rekursiven Aufruf einer Funktion werden die Parameter, Rückgabewerte usw. der Funktion kontinuierlich auf den Stapel verschoben. Funktionsaufrufe verwenden ständig den Stapel, berichten an die Szene und stellen die Szene wieder her, sodass der Speicheraufwand immer größer wird. Die Lösung ist die Schwanzrekursion. PHP hat jedoch keinen Optimierungseffekt auf die Schwanzrekursion, daher ist dies bei dieser Lösung nicht der Fall praktische Bedeutung.
