

Einführung
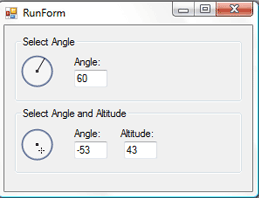
Adobe Photoshop verfügt über zwei sehr professionelle Steuerelemente zum Einstellen von Spezialeffekten wie Schlagschatten, Abschrägung und Relief: Eine davon ist der Winkelwähler und der andere ist der Winkel- und Höhenwähler (wie im Bild oben gezeigt).
Dieser Artikel führt die Leser dazu, zwei benutzerdefinierte Steuerelemente zu erstellen, um das Erscheinungsbild und Verhalten dieser beiden Steuerelemente in Photoshop zu imitieren.
Grundkenntnisse – Mathematik
Satz des Pythagoras
(d. h. Satz des Pythagoras, um den Originaltext zu respektieren, im Folgenden als Satz des Pythagoras bezeichnet. Obwohl er etwas kompliziert ist. — —Anmerkung von Nobi)
Mit dem Satz des Pythagoras können wir die Hypotenuse (längste Seite) eines rechtwinkligen Dreiecks berechnen. Die Berechnungsformel lautet 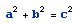 . Auf diese Weise ist die Hypotenuse c gleich
. Auf diese Weise ist die Hypotenuse c gleich  .
.
Einheitskreis
Da sich die nächste Arbeit mit Winkeln und Kreisen befasst, ist es hilfreich, dass wir uns zunächst mit der Form des Einheitskreises vertraut machen. Der Einheitskreis ist ein Kreis mit Mittelpunkt (0,0) und Radius 1. In einem regelmäßigen Raster (bezogen auf die Leinwand – Anmerkung von Nobi) beginnt 0 Grad (die Koordinaten) am Punkt (1,0) (rechts) und nimmt gegen den Uhrzeigersinn zu. Daher sind 90 Grad (0,1), 180 Grad (-1,0), 270 Grad (0,-1) und schließlich fallen 360 Grad mit dem Nullpunkt zusammen.
Trigonometrische Funktionen
Hier müssen wir nur drei grundlegende trigonometrische Funktionen kennen: sin, cos und tan (Sinus, Cosinus und Tangens – Nobi Note). Wenn wir uns an SOH-CAH-TOA (Anmerkung +) erinnern, wissen wir, dass der Sinus eines (rechtwinkligen) Dreiecks gleich dem Verhältnis der gegenüberliegenden Seite zur Hypotenuse ist, der Kosinus ist gleich dem Verhältnis der benachbarten Seite zur Hypotenuse, und der Tangens ist gleich dem Verhältnis der Gegenkathete zur Ankathete.
Ebenso wissen wir, dass inverse trigonometrische Funktionen zur Berechnung unbekannter Winkel verwendet werden.
Anmerkung +:
SOH-CAH-TOA ist eine Formel, die von Ausländern verwendet wird, um sich trigonometrische Funktionen zu merken. Darunter: O ist das Gegenteil (gegenüberliegende Seite), H ist die Hypotenuse (Hypotenuse) und A ist die angrenzende Seite.
SOH: Sinus = Gegenteil ÷ Hypotenuse
CAH: Kosinus = Angrenzend ÷ Hypotenuse
TOA: Tangent = Gegenteil ÷ Angrenzend
Gemeinsame Funktionen
Die folgenden zwei wichtigen Funktionen (Methoden) werden in den von uns erstellten benutzerdefinierten Steuerelementen verwendet:
Eine Funktion empfängt Winkel und Radius als Parameter und gibt den Winkel um einen bestimmten Ursprung zurück. Entsprechender Punktstandort. (Um es einfach auszudrücken: Es wandelt Winkel in Punkte um.)
Eine Funktion, die das Gegenteil vervollständigt und Punkte (X, Y) als Parameter verwendet, um den am besten passenden Winkel zu finden.
Die erste Funktion sollte einfacher sein:
private PointF DegreesToXY(float degrees, float radius, Point origin)
{
PointF xy = new PointF();
double radians = degrees * Math.PI / 180.0;
xy.X = (float)Math.Cos(radians) * radius + origin.X;
xy.Y = (float)Math.Sin(-radians) * radius + origin.Y;
return xy;
}Was Sie zuerst beachten sollten Wir müssen Winkel in Bogenmaß umrechnen. Im Allgemeinen müssen wir nur den Einheitskreis studieren:
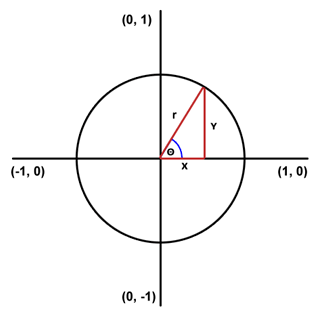
Diese Funktion kennt den Winkel und den Radius. Mithilfe trigonometrischer Funktionen berechnen wir die X- und Y-Werte und dann Fügen Sie einfach die angegebenen Anfangskoordinaten des Ursprungs hinzu.
Sie sollten außerdem beachten, dass im Funktionscode der negative Wert der Y-Komponente verwendet wird. Dies liegt daran, dass das Raster auf dem Computermonitor auf dem Kopf steht (nach unten ist positiv).
Die Funktion der zweiten Funktion besteht darin, die Punktposition, auf die der Benutzer auf das Steuerelement klickt, in den entsprechenden Winkelwert umzuwandeln. Das ist etwas schwieriger, weil wir darüber nachdenken müssen, ein paar Dinge hinzuzufügen. Aufgrund der begrenzten Länge des Artikels habe ich einen Teil des Codes hier gepostet:
private float XYToDegrees(Point xy, Point origin)
{
double angle = 0.0;
if (xy.Y < origin.Y)
{
if (xy.X > origin.X)
{
angle = (double)(xy.X - origin.X) / (double)(origin.Y - xy.Y);
angle = Math.Atan(angle);
angle = 90.0 - angle * 180.0 / Math.PI;
}
else if (xy.X < origin.X)
{
//如此这般
}
}
else if (xy.Y > origin.Y)
{
//如此这般
}
if (angle > 180) angle -= 360; //控制角度范围
return (float)angle;
}Diese Funktion überprüft hauptsächlich die Position der Maus relativ zum Mittelpunkt bestimmen. Sobald wir die Quadranten kennen, können wir die trigonometrische Funktion (Arkustangens) verwenden, um den Winkel zu berechnen.
Wenn der Winkel größer als 180 Grad ist, subtrahieren Sie 360 Grad. Dies ist genau wie Photoshop und steuert den Winkel zwischen -180 Grad und 180 Grad. Natürlich müssen Sie diesen Schritt nicht ausführen. Das Steuerelement kann weiterhin verwendet werden, ohne diese Codezeile hinzuzufügen.
Steuerelemente erstellen
Steuerelemente zeichnen
Die Hintergründe dieser beiden Steuerelemente sind gleich:
Zeichnen Sie die Außenseite mit einem Stift mit einer Breite von 2 Der Kreis
wird mit Weiß bei 40 % (ca. 100) Deckkraft gefüllt
Die Mitte des Steuerelements ist a 3x3 Pixel Quadrat
protected override void OnPaint(PaintEventArgs e)
{
//...
//Draw
g.SmoothingMode = SmoothingMode.AntiAlias;
g.DrawEllipse(outline, drawRegion);
g.FillEllipse(fill, drawRegion);
//...光标
g.SmoothingMode = SmoothingMode.HighSpeed;
g.FillRectangle(Brushes.Black, originSquare);
//...
}注意SmoothMode属性。在绘制圆圈时将该属性设置为AntiAlias(抗锯齿),这样看起来既光滑又专业。但是如果画正方形时也用抗锯齿,就会显得模糊难看,所以将SmoothMode设置为HighSpeed(高速),这样画出的正方形边缘整齐犀利。
根据控件不同,光标也有不同绘制方法。角度选择器比较简单,只需要从圆心到DegreesToXY函数返回的点连一条直线即可。角度与高度选择器则是在这点上绘制一个1x1的矩形,然后在周围绘制一个十字型光标。
处理用户点击
多亏我们有了XYToDegrees函数,处理用户点击变得特别简单。为了让我们的控件用起来和Photoshop一模一样,我们需要设置MouseDown和MouseMove事件。这样,各项数值将实时更新。这里是一个附注函数的代码:
private int findNearestAngle(Point mouseXY)
{
int thisAngle = (int)XYToDegrees(mouseXY, origin);
if (thisAngle != 0)
return thisAngle;
else
return -1;
}高度控件需要额外的处理,就是找到中心点和鼠标点击点的距离:
private int findAltitude(Point mouseXY)
{
float distance = getDistance(mouseXY, origin);
int alt = 90 - (int)(90.0f * (distance / origin.X));
if (alt < 0) alt = 0;
return alt;
}在Photoshop中,选择点(指鼠标点击点)在圆心时,高度为90,在边缘处则为0。这样,我们可以通过找到点击点到圆心距离和半径高度比值来计算出高度。然后,用90减去该值(实际上是按90到0来翻转一下)。
自定义事件
为了让我们的自定义控件更加专业,需要控件能够在数值发生变化时以编程方式进行提醒。这就是我们要设置事件的原因。
例如,像这样给角度变化添加一个事件:
public delegate void AngleChangedDelegate(); public event AngleChangedDelegate AngleChanged;
然后,我们要做的就是每次变更Angle属性时,调用AngleChanged()(需要先判断是否为null)。
限制与改进
闪烁
没有闪烁!只需要在制作控件时设置DoubleBuffered属性为true,.NET Framework 2.0会处理剩下的工作,保证控件能流畅的重绘。
尺寸
因为控件使用基于半径(圆)的数学计算方法,因此需要保证控件的长度和宽度相等。
颜色
我是照着Photoshop的样子来的,所以并没包含背景颜色、外圈颜色这些属性。但是,浏览下代码,你会发现改成你喜欢的颜色或者让颜色可以动态修改并不是什么难事。
结论
我建议你下载项目文件(或者至少下载DEMO),这样你可以看到这俩控件用起来很爽。
协议
本文及有关代码、程序均基于CPOL(Codeproject Open License)协议。
更多Photoshop样式的角度和高度选择器控件 相关文章请关注PHP中文网!




