Zusammenfassung des Algorithmus des Photoshop-Gaußschen Unschärfefilters

Ich war kürzlich von der Forschung einiger Internetnutzer zu Gaußschen Unschärfefiltern beeindruckt und fasse sie hiermit wie folgt zusammen. Gaußsche Unschärfe ist eine Art Verarbeitungsmethode für digitale Bildvorlagen. Seine Vorlage wird auf der Grundlage einer zweidimensionalen Normalverteilungsfunktion (Gaußsche Verteilung) berechnet.
Die Normalverteilung wurde erstmals von A. Demoivre ermittelt, als er die asymptotische Formel der Binomialverteilung fand. C.F. Gauss hat es aus einem anderen Blickwinkel abgeleitet, als er Messfehler untersuchte. P.S. Laplace und Gauss untersuchten seine Eigenschaften. Daher der Name Gaußsche Unschärfe.

Funktionsdefinition der eindimensionalen Normalverteilung:

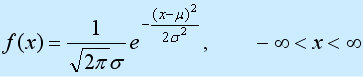
Verteilung von Typ-Zufallsvariablen, der erste Parameter μ ist der Mittelwert der folgenden Zufallsvariablen Bei der Normalverteilung ist der zweite Parameter σ2 die Varianz dieser Zufallsvariablen, daher wird die Normalverteilung als N(μ, σ2) aufgezeichnet. Die Wahrscheinlichkeitsregel einer Zufallsvariablen, die einer Normalverteilung folgt, besagt, dass die Wahrscheinlichkeit, einen Wert in der Nähe von μ anzunehmen, hoch ist und die Wahrscheinlichkeit, einen Wert anzunehmen, der weiter von μ entfernt ist, umso kleiner ist, je kleiner σ ist, desto konzentrierter ist die Verteilung liegt in der Nähe von μ und je größer σ, desto kleiner ist die Streuung. Die Eigenschaften der Dichtefunktion der Normalverteilung sind: Sie ist symmetrisch um μ, erreicht einen Maximalwert bei μ, nimmt im positiven (negativen) Unendlichen den Wert 0 an und hat einen Wendepunkt bei μ±σ. Seine Form ist in der Mitte hoch und auf beiden Seiten niedrig, und das Bild ist eine glockenförmige Kurve über der x-Achse. Wenn μ = 0, σ2 = 1, spricht man von der Standardnormalverteilung und wird als N (0, 1) aufgezeichnet.

Die Bedeutung zweier Konstanten: μ-Erwartung, σ^2-Varianz.

Jetzt lösen wir die erste Frage: Wie groß ist der Radius im Gaußschen Unschärfefilter? Die Antwort ist, dass der Gaußsche Radius in der Formel σ ist.

Die Bedeutung der Form und des Radius der Gaußschen Kurve ist in der folgenden Abbildung dargestellt (Dokumentation von Experten des technischen Supports im Adobe SDK):

> Es ist ersichtlich, dass der Gaußsche Radius ( σ) beeinflusst die Form der Kurve. Je kleiner σ, desto höher und steiler die Kurve. Je größer σ, desto niedriger und sanfter. Bei einem zweidimensionalen Bild handelt es sich um eine glockenförmige Oberfläche. Je kleiner der Gaußsche Radius, desto höher, schärfer und steiler ist die Oberfläche. Daher gilt: Je kleiner der Gaußsche Radius, desto kleiner die Unschärfe, und je größer der Gaußsche Radius, desto größer die Unschärfe. Wir werden sehen, dass ps den Bereich des Gaußschen Radius als [0,1~250] definiert. Wenn der Radius 0,1 beträgt, ist nach der Berechnung nur das mittlere Pixel der Gaußschen Vorlage 1, und die anderen Pixel sind alle = 0 (tatsächlich nähern sie sich gerade 0), dh das Bild ändert sich nicht.

Die zweite Frage ist: Welche Beziehung besteht zwischen der Größe der Gaußschen Vorlage und dem Gaußschen Radius? Das ist ein Missverständnis, das uns schon immer beschäftigt hat. Weil unser Denken in das Missverständnis der physischen Umsetzung geraten ist. In der physischen Implementierung ist die Gaußsche Vorlage begrenzt, was dazu führt, dass wir die eigentliche Antwort auf diese Frage ignorieren: Die Gaußsche Vorlage ist logisch unbegrenzt. Das heißt, die Gaußsche Vorlage ist im Wesentlichen eine Näherung einer logisch unendlichen ausgedehnten Oberfläche. Daher sollte die Vorlagengröße als unendlich betrachtet werden. Es ist nur so, dass wir bei der Berechnung diese Werte unterhalb eines bestimmten Schwellenwerts nicht mehr berücksichtigen, da sie sich in der Entfernung 0 nähern. Dieser Schwellenwert ist die Vorlagengrenze.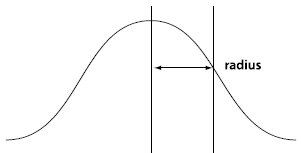

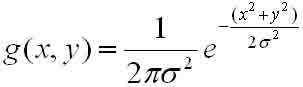
Das Folgende ist die Formel für eine zweidimensionale Gaußsche Oberfläche (x, y stellen die Vorlagenkoordinaten des Pixels dar und die Position der Vorlagenmitte ist der Ursprung):

🎜>

Das heißt: g(x,y)= ( 1 / (2*pi*σ^2) ) * exp( -(x^2+y^2)/ (2*σ^2 ) ;

Basierend auf dieser Formel können wir die Gaußschen Vorlagen unter verschiedenen Radien berechnen. Tatsächlich sind die Vorlagen unendlich, aber sie nähern sich 0 weit vom Zentrum entfernt Beispielsweise berechnen wir r Eine normalisierte Gaußsche Vorlage, wenn =0,7:

高斯模板（guass radius=0.700000）
//Guass-Radius=0,700000
0,000000    0,000000   0,000000   0,000000   0,000000   0,000000   0,000000   0,000000   0,000000   
0,000000   0,000000   0,000001   0. 000012    0,000033   0,000012   0,000001   0,000000   0,000000   
0,000000   0,000001 0,000093   0,001976   0,005481   0,001976   0,000093   0,000001   0,000000   
0,000000   0,000012   0,001976   0,042189   0,117046   0,042189   0,001976   0,000012   0,000000   
0,000000   0,000033   0,005481   0,117046   0,324724   0,117046   0,005481   0. 000033   0,000000   
0,000000   0,000012   0,001976   0,042189   0,117046   0,042189   0,001976   0,000012   0,000000   
0,000000    0,000001   0,000093   0,001976   0. 005481   0,001976   0,000093   0,000001    0,000000   
0,000000   0,000000   0,000001   0,000012   0,000033   0,000012   0,000001   0,000000   0,000000   
0,000000   0. 000000    0,000000   0,000000   0,000000   0,000000   0,000000   0,000000   0,000000  

 

        个整数除法形式的近似：

         1 2 1

         2 4 2    /16

         1 2 1

Tatsächliche Überprüfung: Wir haben festgestellt, dass diese 3*3-Vorlage tatsächlich eine Näherung ist, wenn der Gaußsche Radius etwa 0,849 beträgt. Wenn r=0,849, ist seine 3*3-normalisierte Vorlage (geben Sie in MATLAB h=fspecial( ein). 'gaußian', 3, 0.849); um diese Vorlage zu erhalten):

0.062467 0.125000 0.062467 0.125000 0.250131 0.125000 0.062467 0. 125000 0 .062467


Dann können wir imfilter in Matlab verwenden, um eine Gaußsche Unschärfeverarbeitung für das Bild durchzuführen:

img = imread('c:demo.bmp');

h = fspecial('gaußian', 3, 0.849); img2 = imfilter(img, h); subplot(121), imshow(img); title('Originalbild') subplot(122), imshow(img2); title('Nach Gaußscher Unschärfe')



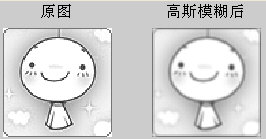
Der Effekt ist wie folgt:

Wir können es in Matlab wie folgt verwenden: Anweisung „Gaußsche Fläche zeichnen“:

Matlab-Code zum Zeichnen von Gaußscher Fläche Oberfläche

Code-Hervorhebung erstellt mit Actipro CodeHighlighter (Freeware)http:// www.php.cn/

%

Zeichnen Sie eine Gaußsche Unschärfeoberfläche!
------r=
0,849 ; %Gaußscher Radius (von 0,1 bis 250) x=-
3 :0,2:3;y=
x ;[X,Y]=
meshgrid(x,y);Z=
exp(-(X.^2+Y.^ 2)./(2*r *r))/(2*pi*r*r);mesh(X,Y,Z)
Der Effekt ist wie folgt Bild:

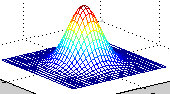                                                           > Aus der Frequenzbereichskurve ist ersichtlich, dass die Gaußsche Unschärfe im Wesentlichen ein Tiefpassfilter ist. Bei der Bildverarbeitung werden hochfrequente Informationen an Stellen mit drastischen Graustufenänderungen wie den Bildrändern herausgefiltert.

Abschließend geben wir den C-Sprachcode zur Berechnung der Gaußschen Unschärfevorlage an. Bitte beachten Sie, dass wir tatsächlich nur etwa 1/4 der Vorlage berechnen müssen, da die Gaußsche Vorlage symmetrisch ist. Aber wir haben hier keine solche Optimierung im Code vorgenommen. Die von uns ausgegebene Vorlage ist (2*N+1)*(2N+1) und der Gaußsche Radius wird durch r dargestellt.

Gaußsche Vorlage berechnen
#include math.h>
#include stdio.h>
#define N 3 3 🎜>/ * Vorlagengröße: (2N+1) * (2N+1) */
void main(){

doppelta[2*N+1][2*N+1] /* Gauß template*/ 
double r=0.6; /* Gaußscher Radius: [ 0,1, 250] */ 
doppelt A=1/ (2*M_PI*r*r); int
i,j; 
for (i=-1*N;iN;i++) für
(j=-1*N;jN;j++ )a[i+N][j+N]=A*exp((-1)*( i*i+j*j) / (2*r*r));
}

Gleichzeitig geben wir zum Vergleich den Code zum Generieren von Gaußschen Vorlagen in Matlab (den Codeteil von fspecial, Dabei ist p3 der Die drei Parameter sind der Gaußsche Radius):

  case 'gaussian' % Gaussian filter

     siz   = (p2-1)/2;  %注：p2即模板边长，默认值为33
     std   = p3;        %注：p3即高斯半径，默认为为0.5
     
     [x,y] = meshgrid(-siz(2):siz(2),-siz(1):siz(1));
     arg   = -(x.*x + y.*y)/(2*std*std);

     h     = exp(arg);
     h(h<eps*max(h(:))) = 0;

     sumh = sum(h(:));  %注：模板归一化
     if sumh ~= 0,
       h  = h/sumh;
     end;

Weitere verwandte Artikel zur Algorithmuszusammenfassung des Photoshop-Gaußschen Unschärfefilters finden Sie auf der chinesischen PHP-Website!