Wie das Sprichwort sagt: Wenn Sie Bilder posten, ohne Samen zu hinterlassen, werden Tausende von Menschen die Chrysanthemen erstechen! Ich möchte das noch etwas erweitern: Wer im Unterricht keine Beispiele nennt, wird als Narr abgestempelt! Ups, es reimt sich ziemlich viel, hehe, nur ein Scherz!
Wir haben in vier Ausgaben über das Wissen über API gesprochen. Das vorherige kleine Beispiel ist zu einfach und löscht Ihren Durst nicht Atem, lassen Sie mich Ihnen unten ein kleines Beispiel geben, um Ihren Geist aufzufrischen!
Als ich vorhin über das Zeichnen eines Kreises sprach, kam mir ein Gedanke bzw. eine Falle in den Sinn: Wie zeichnet man eine Fächerform? Wir wissen, dass die Methode zum Zeichnen eines Kreises nicht auf einmal möglich ist. Ich weiß nicht, ob Sie einen Eindruck davon haben Nochmals: Wenn ich einen Bogen zeichne, dann zeichne ich zwei Linien in der Mitte des Kreises und verbinde sie jeweils mit dem Startpunkt und dem Endpunkt des Bogens. Ist das dann nicht ein Kreis? Kann diese Methode also einen Kreis zeichnen? Eigentlich weiß ich es nicht, also versuchen wir es:
Der erste Schritt besteht darin, einen Bogen zu zeichnen:
//将原点移到100,100的位置 ctx.translate(100, 100); //画一个圆弧 ctx.arc(0,0,100,30*Math.PI/180, 60*Math.PI/180); ctx.stroke();
At Diesmal ist es die Methode zum Zeichnen von Bögen, die wir kennen. Jetzt müssen wir mit dem Zeichnen von Linien beginnen. Das ist der Schlüssel zum Schärfen eines Messers.
Eine gerade Linie besteht aus 2 Punkten. Da wir nun den Mittelpunkt des Kreises kennen, ist der zweite Punkt der Start- und Endpunkt des Bogens ? Lassen Sie uns ein Bild zeichnen, um es zu analysieren: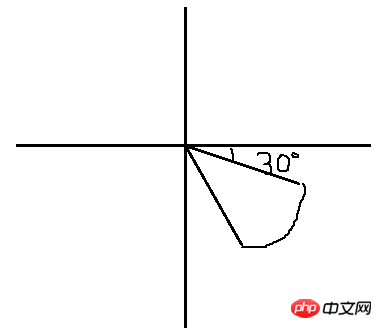 
Wir wollen wahrscheinlich eine solche Fächerform zeichnen, die ziemlich hässlich ist. Schauen wir uns das an und verwenden Sie die Winkelformel 1. Durch allgemeine Berechnungen können wir möglicherweise die Koordinaten dieser beiden Punkte ermitteln, aber selbst wenn ich darüber nachdenke, habe ich das Gefühl, wie dupliziert diese Berechnung ist. Ich bin nicht gut in Mathematik nicht bereit, Berechnungen durchzuführen. Gibt es eine einfache Möglichkeit, dies zu tun, ohne dies tun zu müssen? (Sorry, mein „Gedächtnis“ reicht offensichtlich nicht aus) Ich habe eine gewagte Hypothese, nämlich wenn die Fächerform nicht so schräg ist, sondern auf einer Seite horizontal, zum Beispiel: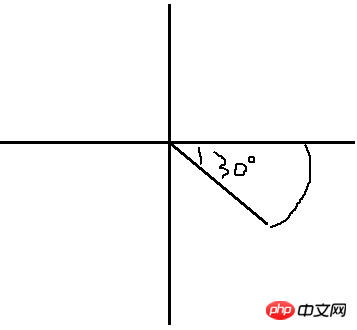 
Dann kann ich leicht das erste Liniensegment bekommen, das ist die Linie auf der Abszisse, verstehst du nicht? Okay, es ist so, wir kennen die Koordinaten des Kreismittelpunkts, wir kennen den Radius, dann sind die Koordinaten des Startpunkts des Bogens sehr einfach. Verstehen Sie, wie bekommt man die andere Linie? Wenn Sie gerade das Wissen über die API in der letzten Ausgabe gelesen haben, können wir uns die Methode „rotate()“ leicht vorstellen, solange sie noch heiß ist. Das heißt, wir zeichnen eine weitere Linie vom Mittelpunkt des Kreises zum Startpunkt Kennen Sie den Winkel des Bogens? Okay, wir werden es tun. Wenn Sie den Winkel des Bogens für diese neu gezeichnete Linie wählen, wird sie dann nicht den Endpunkt erreichen? Verdammt, ich bin so verdammt schlau! Probieren wir es aus:
//圆弧 ctx.save(); ctx.translate(100, 100); ctx.arc(0,0,100,0, 30*Math.PI/180); ctx.restore(); //第一条线 ctx.save(); ctx.moveTo(100,100); ctx.lineTo(200,100); ctx.restore(); //第二条线 ctx.save(); ctx.translate(100, 100); ctx.moveTo(0,0); ctx.rotate(30*Math.PI/180); ctx.lineTo(100,0); ctx.stroke(); ctx.restore();
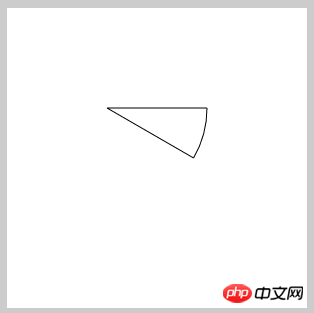
Wow, nach dieser Idee funktioniert es wirklich, wenn wir das jetzt drehen Sektor um einen Winkel. Dieser Winkel = der Winkel der zweiten Linie - der Winkel der ersten Linie. Ist es dann nicht der Sektor, den wir brauchen? Aber die direkte Drehung des vorherigen Codes kann nur Bögen drehen, nicht Linien. Ändern wir es:
Schauen wir uns dieses Bild an, wir können unser Denken ändern. Wenn der Bogen an der Zielposition gezeichnet wird, werden zwei Linien mit einem Winkel von 0 gezeichnet und dann zum Start- und Endpunkt des Bogens gedreht. Wäre das nicht ausreichend? (Weil wir den Anfangs- und Endwinkel des Bogens kennen) Probieren Sie es aus:
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100，则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.stroke();
哎呀，真的可以啊，哈哈，有人会问，你的第一步为什么是设置原点呢，为什么不用moveTo来设置起始点呢？好问题，因为画布的默认原点在0,0的位置上，如果用moveTo来设置起始点，原点依然还在0,0的位置，上一节API我们将变换的时候讲到，变换是以原点为基准点的，即使你设置了起始点，但是起始点不是原点的话，图形旋转依然会围绕0,0点旋转然后自转，得到的图形就不知道是什么图形了，偏差的角度就很难矫正，对此还是不太明白的同学可以自己写一个例子体验一样，或许理解更深刻一点，这里就作为练习题，不在这里写了！
上面的代码还是可以优化的，比如说画第一条线的时候，我们用到了save()和restore()，其作用不只是可以防止外面的属性或方法对里面的绘制产生影响，它的本质意思是save()保存当前环境的状态，restore()返回之前保存路径的状态，这是什么意思，举个栗子，save()就像是在一个迷宫的入口，restore()就想是这个迷宫的出口，但是发现这里就是迷宫的路口，出了迷宫，在迷宫里具体是怎么走的，根本不知道，这就可以防止你的外部因素来影响你走迷宫的路线，那有一个细节大家要注意，就是当你进去的这个门，你出来的时候还是这个门，恩，这个就可以利用了，这就相当于是画笔的触点了，还原触点，我们看一下还原的触点在什么地方：
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100，则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(0,0); ctx.lineTo(100,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.lineTo(100,0); ctx.stroke();
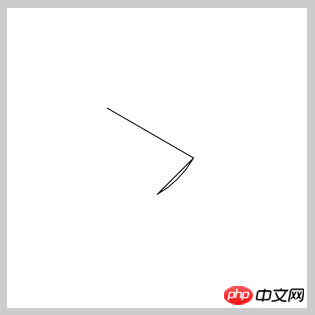
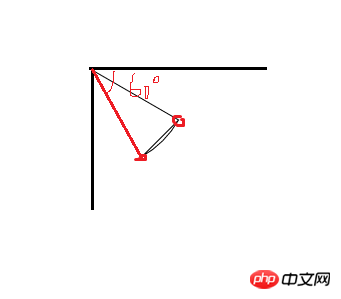
居然得到的是这样的结果，从第2张图可以看出还原的触点的位置在圆弧的初始点，其实这里我们是忽略了一个问题，就是线在旋转的时候，是从它的起点为圆心旋转的，而上面的代码是，第一条线从圆心开始，到圆弧的起点（旋转过后），自然现在的起点就是圆弧的起点了，第二条线怎么画，它旋转的结果都不是我们想要的了，所以这里我们需要特别的注意，现在我们将第一条直线的起点设在（r,0）的位置，旋转后就到了圆弧的起始点，然后在画到圆心地方，那现在的起始点就是圆心了，再画一条线到圆弧，就哦了，现在我们再来一次：
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100，则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //save(),restore()是为了防止角度旋转的污染 ctx.save(); ctx.rotate(30*Math.PI/180); ctx.moveTo(100,0); ctx.lineTo(0,0); ctx.restore(); ctx.rotate(60*Math.PI/180); ctx.lineTo(100,0); ctx.stroke();
看，这就是我们想要的图形，所以，上面所犯的几个错都是比较容易犯的错，需要特别的注意！
根据这个原理，我们其实还可以用另外一种方式，就是充分使用触点的作用，怎么讲，当我们再画圆弧的时候，画完之后其触点在圆弧的结束位置，如此的天赐良机，为何不直接将这个触点作为起点，画一条到圆心的线，不就可以少旋转一次吗？然后再画第二条线，简直感觉省时省力，我们看看效果吧：
//将原点设置100,100位置 ctx.translate(100,100); //原点在100,100，则圆心设为0,0 ——> 100,100的位置 ctx.arc(0,0,100,30*Math.PI/180,60*Math.PI/180); //以圆弧终点为起点画直线 ctx.lineTo(0,0); ctx.rotate(30*Math.PI/180); //以0,0为起点画直线 ctx.lineTo(100,0); ctx.stroke();
你看，用这个理论，就连save(),restore()都可以省了，因为就只有一个旋转，代码也少了好多，效果还一样，哈哈，为了能重复使用，我们需要把他封装一下：
第一种：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
this.save();
this.translate(x,y);
this.beginPath();
this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
this.save();
this.rotate(sDeg*Math.PI/180);
this.moveTo(r,0);
this.lineTo(0,0);
this.restore();
this.rotate(eDeg*Math.PI/180);
this.lineTo(r,0);
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();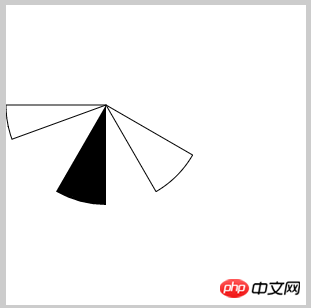
第二种：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,sDeg,eDeg){
this.save();
this.translate(x,y);
this.beginPath();
this.arc(0,0,r,sDeg*Math.PI/180,eDeg*Math.PI/180);
this.lineTo(0,0);
this.rotate(sDeg*Math.PI/180);
this.lineTo(r,0);
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();
你以为这样就完了吗？当我们充分理解canvasAPI的基础知识的时候，我们还会得到另外一种方式来画扇形，简直6到爆！哈哈哈！究竟是什么呢？我们接着往下看：
前面的基础知识讲到画圆的时候，我们讲到了beginPath()和closePath()，有人会说，这不就是开始路径和封闭路径吗？这跟画扇形有什么关系？没错，你说的一点都没错，好，现在请大声跟我念：封闭路径！封闭路径！封闭路径！重要事情说3遍，现在你的心里是不是有了那么一点感觉，没错，不要觉得害羞，不要觉得压抑，就是它，就是它，大声把它说出来，就是这感觉，什么？你什么感觉都没有，此处有表情，好吧，我来告诉你我的感觉：
上面有一处说，为什么要用translate，而不要moveTo，是因为我们需要旋转，所以就需要原点，现在如果我们不需要旋转，而是正常的画图，那么我们就不需要原点，我们就可以用moveTo，好了，如果我们配合beginPath()和closePath()，就会将一个圆弧封闭起来，想想我们在讲画三角形的时候的那段折线是怎么变成三角形的，没错，现在是否有了一点感觉？还是木有？好吧，我们来看一个栗子：
ctx.beginPath(); //定义起点 ctx.moveTo(100,100); //以起点为圆心，画一个半径为100的圆弧 ctx.arc(100,100,100,30*Math.PI/180, 60*Math.PI/180); ctx.closePath(); ctx.stroke();
看看，寥寥数行，就画出了一个扇形，对不上面的图像，是不是一样的？我们封装一下：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.sector(100,100,100,30,60).stroke();
ctx.sector(100,100,100,90,120).fill();
ctx.sector(100,100,100,160,180).stroke();
效果都一样，只是思路不一样，或许还有别的方式来画扇形，如果大家有更好的方法，希望能留下你的代码，大家互相学习一下！
扇形的方法有了，具体用哪个可以依据自己的喜好，我就按照第3种来写一个小应用，饼图：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.fillStyle = 'red';
ctx.sector(200,200,100,30,150).fill();
ctx.fillStyle = 'green';
ctx.sector(200,200,100,150,270).fill();
ctx.fillStyle = 'blue';
ctx.sector(200,200,100,270,390).fill();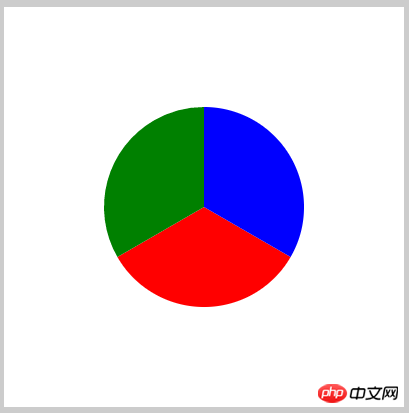
再写一个扇形倒计时：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
var angle = 0;
var timer = null;
ctx.fillStyle = 'green';
setInterval(function(){
angle+=5;
ctx.sector(200,200,100,0,angle).fill();
if(angle == 360){
clearInterval(timer);
}
},200);
你以为我只是写几个例子给你看吗？你还是太年轻了，之所以要丢出这2个例子，是为了扩展一下思路，我们可以在这些效果上面加一点什么东西，效果是否就不一样了，举个例子，第一个饼图，如果我们在中间加一个白色的圆，会怎么样？
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
ctx.fillStyle = 'red';
ctx.sector(200,200,100,30,150).fill();
ctx.fillStyle = 'green';
ctx.sector(200,200,100,150,270).fill();
ctx.fillStyle = 'blue';
ctx.sector(200,200,100,270,390).fill();
ctx.fillStyle = '#fff';
ctx.sector(200,200,80,0,360).fill();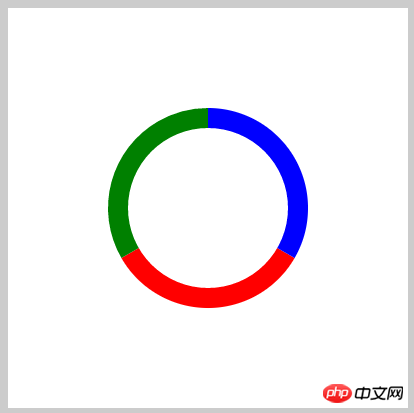
看，这效果是不是就变成另外一个效果了，比如说第二个效果，我们也加一个白色的圆，看有什么效果：
CanvasRenderingContext2D.prototype.sector = function(x,y,r,angle1,angle2){
this.save();
this.beginPath();
this.moveTo(x,y);
this.arc(x,y,r,angle1*Math.PI/180,angle2*Math.PI/180,false);
this.closePath();
this.restore();
return this;
}
var angle = 0;
var timer = null;
setInterval(function(){
angle+=5;
ctx.fillStyle = 'green';
ctx.sector(200,200,100,0,angle).fill();
ctx.fillStyle = '#fff';
ctx.sector(200,200,80,0,360).fill();
if(angle == 360){
clearInterval(timer);
}
},200);
看看，这效果是不是可以做很多的效果，当然，因为没有加动画效果，现在的效果很生硬，需要大家来完善，只要你脑洞打开，其实扇形还是能做出很多非常炫酷的效果的，当然了，好的效果都是需要打磨的，在此只是抛砖引玉，如果大家有更好，更炫酷的效果，请不吝分享一下，今天就讲到这里，谢谢大家的支持！
以上就是canvas实践小实例二 —— 扇形 的内容，更多相关内容请关注PHP中文网（www.php.cn）！
