So verwenden Sie das Heapq-Modul in Python

Das Heapq-Modul stellt Heap-Algorithmen bereit. heapq ist eine Baumdatenstruktur, in der untergeordnete Knoten und übergeordnete Knoten sortiert sind. Dieses Modul stellt heap[k]

Heapq-Typ drucken

import math 
import random
from cStringIO import StringIO

def show_tree(tree, total_width=36, fill=' '):
   output = StringIO()
   last_row = -1
   for i, n in enumerate(tree):
     if i:
       row = int(math.floor(math.log(i+1, 2)))
     else:
       row = 0
     if row != last_row:
       output.write('\n')
     columns = 2**row
     col_width = int(math.floor((total_width * 1.0) / columns))
     output.write(str(n).center(col_width, fill))
     last_row = row
   print output.getvalue()
   print '-' * total_width
   print 
   return

data = random.sample(range(1,8), 7)
print 'data: ', data
show_tree(data)

Ergebnis drucken

data: [3, 2, 6, 5, 4, 7, 1]

     3           
  2      6      
5    4  7     1   
-------------------------
heapq.heappush(heap, item)

Schieben Sie ein Element in den Heap und ändern Sie den obigen Code

heap = []
data = random.sample(range(1,8), 7)
print 'data: ', data

for i in data:
  print 'add %3d:' % i
  heapq.heappush(heap, i)
  show_tree(heap)

Drucken Sie das Ergebnis aus

data: [6, 1, 5, 4, 3, 7, 2]
add  6:
         6         
 ------------------------------------
add  1:
      1 
   6         
------------------------------------
add  5:
      1 
   6       5       
------------------------------------
add  4:
        1 
    4       5       
  6
------------------------------------
add  3:
        1 
    3       5       
  6    4
------------------------------------
add  7:
        1 
    3        5       
  6    4    7
------------------------------------
add  2:
        1 
    3        2       
  6    4    7    5
------------------------------------

Anhand der Ergebnisse können wir verstehen, dass die Elemente des untergeordneten Knotens größer sind als die Elemente des übergeordneten Knotens. Geschwisterknoten werden nicht sortiert.

heapq.heapify(list)

Konvertieren Sie den Listentyp in Heap und ordnen Sie die Liste in linearer Zeit neu an.

print 'data: ', data
heapq.heapify(data)
print 'data: ', data

show_tree(data)

Ergebnis drucken

data: [2, 7, 4, 3, 6, 5, 1]
data: [1, 3, 2, 7, 6, 5, 4]

      1         
   3         2     
7    6    5    4  
------------------------------------
heapq.heappop(heap)

Löschen Sie den kleinsten Wert und geben Sie ihn zurück im Heap Die Elemente werden über heapify() und heappop() sortiert.

data = random.sample(range(1, 8), 7)
print 'data: ', data
heapq.heapify(data)
show_tree(data)

heap = []
while data:
  i = heapq.heappop(data)
  print 'pop %3d:' % i
  show_tree(data)
  heap.append(i)
print 'heap: ', heap

Ergebnisse drucken

data: [4, 1, 3, 7, 5, 6, 2]

         1
    4         2
  7    5    6    3
------------------------------------

pop  1:
         2
    4         3
  7    5    6
------------------------------------
pop  2:
         3
    4         6
  7    5
------------------------------------
pop  3:
         4
    5         6
  7
------------------------------------
pop  4:
         5
    7         6
------------------------------------
pop  5:
         6
    7
------------------------------------
pop  6:
        7
------------------------------------
pop  7:

------------------------------------
heap: [1, 2, 3, 4, 5, 6, 7]

Sie können sehen, dass es so ist Der sequentielle Heap wurde in die Warteschlange gestellt.

heapq.heapreplace(iterable, n)

Entfernt das vorhandene Element und ersetzt es durch einen neuen Wert.

data = random.sample(range(1, 8), 7)
print 'data: ', data
heapq.heapify(data)
show_tree(data)

for n in [8, 9, 10]:
  smallest = heapq.heapreplace(data, n)
  print 'replace %2d with %2d:' % (smallest, n)
  show_tree(data)

Ergebnisse drucken

data: [7, 5, 4, 2, 6, 3, 1]

         1
    2         3
  5    6    7    4
------------------------------------

replace 1 with 8:

         2
    5         3
  8    6    7    4
------------------------------------

replace 2 with 9:

         3
    5         4
  8    6    7    9
------------------------------------

replace 3 with 10:

         4
    5         7
  8    6    10    9
------------------------------------

heapq.nlargest (n, iterable) und heapq.nsmallest(n, iterable)

geben die n Maximal- und Minimalwerte in der Liste zurück

data = range(1,6)
l = heapq.nlargest(3, data)
print l     # [5, 4, 3]

s = heapq.nsmallest(3, data)
print s     # [1, 2, 3]

PS: Ein Berechnungsproblem
Erstellen eines Minimum-Heap-Codebeispiels mit der Anzahl der Elemente K=5:

#!/usr/bin/env python 
# -*- encoding: utf-8 -*- 
# Author: kentzhan 
# 
 
import heapq 
import random 
 
heap = [] 
heapq.heapify(heap) 
for i in range(15): 
 item = random.randint(10, 100) 
 print "comeing ", item, 
 if len(heap) >= 5: 
  top_item = heap[0] # smallest in heap 
  if top_item < item: # min heap 
   top_item = heapq.heappop(heap) 
   print "pop", top_item, 
   heapq.heappush(heap, item) 
   print "push", item, 
 else: 
  heapq.heappush(heap, item) 
  print "push", item, 
 pass 
 print heap 
pass 
print heap 
 
print "sort" 
heap.sort() 
 
print heap

Ergebnis:

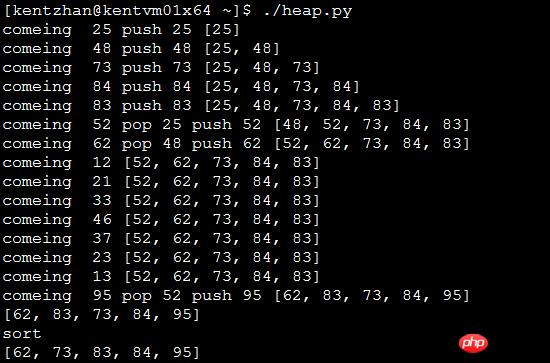
Weitere Artikel zur Verwendung des Heapq-Moduls in Python finden Sie auf der chinesischen PHP-Website!