Einfache Auswahlsortierung ist eine Art Auswahlsortierungsalgorithmus. Grundidee: In jedem Durchgang wird aus den zu sortierenden Datensätzen der Datensatz mit dem kleinsten Schlüsselwort ausgewählt und die Reihenfolge wird am Ende der sortierten Datensatzfolge platziert, bis die gesamte Sortierung abgeschlossen ist. Da sich in jeder Schleife die Positionen von Elementen mit gleichen Werten ändern, handelt es sich um eine instabile Sortierung.
---------------- ------ -----------
Wie unten gezeigt:
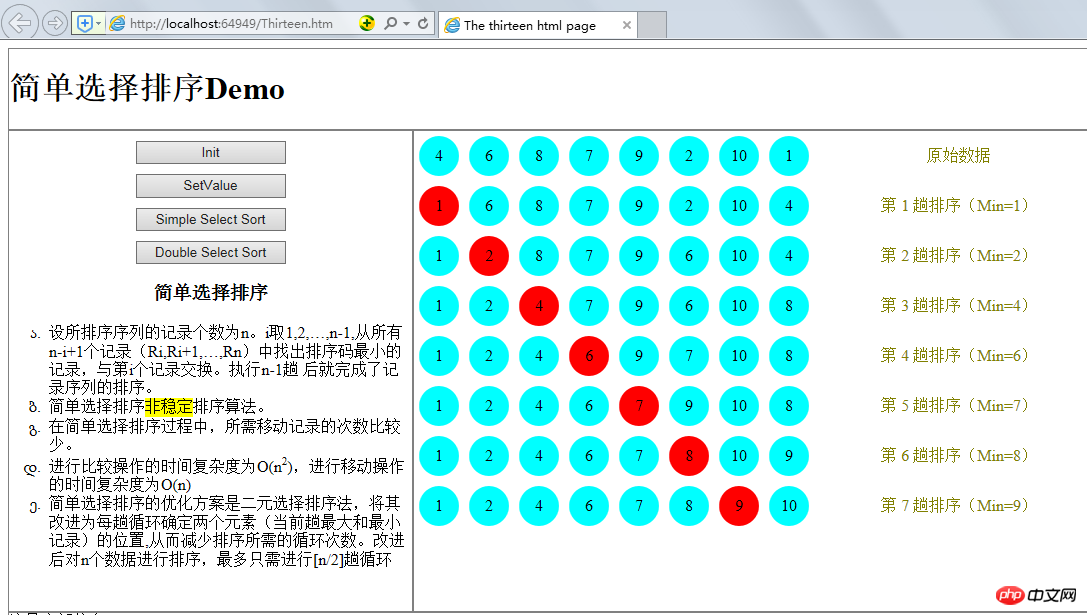
Die Optimierungslösung für die einfache Auswahlsortierung besteht in der Verwendung der binären Auswahlsortierung, die verbessert wird, um die Positionen von zwei Elementen (dem größten und dem kleinsten Datensatz im aktuellen Zyklus) in jedem Zyklus zu bestimmen und dadurch die Anzahl zu reduzieren Anzahl der für die Sortierung erforderlichen Zyklen. Nach der Verbesserung sind zum Sortieren von n Daten höchstens [n/2] Schleifen erforderlich.
Wie in der folgenden Abbildung gezeigt:
Das Prinzip des Algorithmus wird nicht im Detail beschrieben. Verwenden Sie Html5, um eine einfache Auswahl zu implementieren Der Sortieralgorithmus und der Demonstrationscode lauten wie folgt:
<!DOCTYPE html>
<html>
<head>
<title>The thirteen html page</title>
<style type="text/css">
ul li
{
list-style-type:georgian;
text-align:left;
}
.mark
{
width:280px;
height:40px;
color:Olive;
text-align:center;
line-height:40px;
margin:5px;
float:left;
}
.redball
{
width:40px;
height:40px;
border-radius:20px;
background-color:Red;
text-align:center;
line-height:40px;
margin:5px;
float:left;
}
.ball
{
width:40px;
height:40px;
border-radius:20px;
background-color:Aqua;
text-align:center;
line-height:40px;
margin:5px;
float:left;
}
.line
{
clear:left;
}
header
{
height:80px;
border:1px solid gray;
}
.left
{
border:1px solid gray;
float:left;
width:30%;
height:480px;
margin-left:0px;
margin-right:0px;
}
aside
{
text-align:center;
}
section
{
width:69.5%;
float:left;
height:480px;
border:1px solid gray;
margin-left:0px;
margin-right:0px;
}
footer
{
clear:left;
height:60px;
border:1px solid gray;
}
input[type="button"]
{
width:150px;
text-align:center;
margin-top:10px;
}
</style>
<script type="text/javascript">
function initDiv() {
var mainArea = document.getElementById("mainArea");
var childs = mainArea.childNodes;
//添加节点之前先删除,应该从后往前删除，否则节点移动，只能删除一半
for (var i = childs.length - 1; i >= 0; i--) {
mainArea.removeChild(childs[i]);
}
for (var i = 0; i < 8; i++) {
var newDivLine = document.createElement("div");
newDivLine.setAttribute("class", "line");
newDivLine.setAttribute("id", i);
mainArea.appendChild(newDivLine);
for (var j = 0; j < 9; j++) {
var newDiv = document.createElement("div");
var id = i.toString() + j.toString();
newDiv.setAttribute("id", id);
if (j < 8) {
newDiv.setAttribute("class", "ball");
} else {
newDiv.setAttribute("class", "mark");
}
newDivLine.appendChild(newDiv);
}
}
}
//初始元素赋值
function setElementsValue() {
var arrTmp = [4, 6, 8, 7, 9, 2, 10, 1];
for (var i = 0; i < arrTmp.length; i++) {
document.getElementById("0" + i.toString()).innerText = arrTmp[i];
}
document.getElementById("08").innerText = "原始数据";
}
//简单选择排序
function setSimpleSortValue() {
var arrTmp = [4, 6, 8, 7, 9, 2, 10, 1];
var m = 0;//表示要交换的最小坐标
for (var i = 0; i < arrTmp.length-1; i++) {
m = i;
for (var j = i + 1; j < arrTmp.length; j++) {
if (arrTmp[m] > arrTmp[j]) {
m = j;
}
}
if (arrTmp[i] > arrTmp[m]) {
var tmp = arrTmp[m];
arrTmp[m] = arrTmp[i];
arrTmp[i] = tmp;
}
//显示出来
for (var k = 0; k < arrTmp.length; k++) {
document.getElementById((i+1).toString() + k.toString()).innerText = arrTmp[k];
if (i == k) {
document.getElementById((i + 1).toString() + (k).toString()).setAttribute("class", "redball");
} else {
document.getElementById((i + 1).toString() + (k).toString()).attributes["class"].nodeValue="ball";;
}
}
document.getElementById((i+1).toString() + "8").innerText = "第 " + (i+1).toString() + " 趟排序（Min=" + arrTmp[i] + "）";
}
}
//二元选择排序
function setDoubleSelectSort() {
var arrTmp = [4, 6, 8, 7, 9, 2, 10, 1];
selectSortB(arrTmp);
var len=arrTmp.length;
for (var i = (len / 2)+1; i < len; i++) {
for (var j = 0; j < 8; j++) {
document.getElementById((i).toString() + (j).toString()).innerText = "";
document.getElementById((i).toString() + (j).toString()).className="ball";
}
document.getElementById(i.toString() + "8").innerText = "";
}
}
//二元选择排序（升序)
function selectSortB(a) {
var len = a.length;
var temp, min, max;
for (var i = 0; i < len / 2; i++) {
min = i; max = i;
for (var j = i + 1; j <= len - 1 - i; j++) {
max = (a[j] > a[max]) ? j : max;//每一趟取出当前最大和最小的数组下标
min = (a[j] < a[min]) ? j : min;
};
temp = a[i];//先放小的
a[i] = a[min];
if (i == max) { //最大数在数组头部
if ((len - i - 1) !== min) {//最大数在头部,最小数在尾部
a[min] = a[len - i - 1];
}
a[len - i - 1] = temp;
}
else if ((len - i - 1) === min) {//最大数不在头部,最小数在尾部
a[len - i - 1] = a[max];
a[max] = temp
}
else {
//如果最大数在尾部,也是成立的,不用特殊讨论
a[min] = temp;
temp = a[len - i - 1];
a[len - i - 1] = a[max];
a[max] = temp;
}
//显示出来
for (var k = 0; k < a.length; k++) {
document.getElementById((i + 1).toString() + k.toString()).innerText = a[k];
if (i == k || len - i - 1 == k) {
document.getElementById((i + 1).toString() + (k).toString()).setAttribute("class", "redball");
} else {
document.getElementById((i + 1).toString() + (k).toString()).className = "ball";
}
}
document.getElementById((i + 1).toString() + "8").innerText = "第 " + (i + 1).toString() + " 趟排序（Min=" + a[i] + ",Max=" + a[len-i-1] + "）";
}
}
</script>
</head>
<body>
<header>
<h1>简单选择排序Demo</h1>
</header>
<aside class="left">
<input type="button" id="btnInit" value="Init" onclick="initDiv();" />
<br />
<input type="button" id="btnSetValue" value="SetValue" onclick="setElementsValue();" />
<br />
<input type="button" id="btnSimpleSort" value="Simple Select Sort" onclick="setSimpleSortValue();" />
<br />
<input type="button" id="btnDoubleSelect" value="Double Select Sort" onclick="setDoubleSelectSort();" />
<br />
<h3>简单选择排序</h3>
<ul>
<li>设所排序序列的记录个数为n。i取1,2,…,n-1,从所有n-i+1个记录（Ri,Ri+1,…,Rn）中找出排序码最小的记录，与第i个记录交换。执行n-1趟 后就完成了记录序列的排序。</li>
<li>简单选择排序<mark>非稳定</mark>排序算法。</li>
<li>在简单选择排序过程中，所需移动记录的次数比较少。</li>
<li>进行比较操作的时间复杂度为O(n<sup>2</sup>)，进行移动操作的时间复杂度为O(n)</li>
<li>简单选择排序的优化方案是二元选择排序法，将其改进为每趟循环确定两个元素（当前趟最大和最小记录）的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序，最多只需进行[n/2]趟循环</li>
</ul>
</aside>
<section id="mainArea"></section>
<footer>
这是底部信息
</footer>
</body>
</html>Ansicht Code
Über 2 Spezielle Verarbeitung der Metaauswahlsortierung:
Im Allgemeinen reicht ein einfacher Austausch aus.
Sonderfälle treten auf, wenn vier Werte gleich sind, z. B. a[i]=a[max], a[len-1-i]=a[min].
Im Code habe ich mich dafür entschieden, zuerst a[i] den Mindestwert min zuzuweisen und gleichzeitig den Wert von a[i] herauszunehmen, und habe dann drei Situationen im Code
① besprochen: Wenn max ist Wenn sich der Kopf des Arrays am Anfang des Arrays befindet, wird die Situation, ob sich Min am Ende des Arrays befindet, unter der Bedingung ①
② besprochen: Wenn sich Min am Ende des Arrays befindet (und max ist nicht am Kopf des Arrays)
③: Im Allgemeinen gilt das Gleiche [min ist am Kopf des Arrays, max ist am Ende des Arrays]
Weitere Informationen Verwandte Artikel zur Verwendung von HTML5 zur Implementierung einfacher Auswahlsortierungsalgorithmen und Demonstrationen. Bitte beachten Sie die chinesische PHP-Website!
Was sind die Produktionsmethoden der HTML5-Animationsproduktion?
Der Unterschied zwischen HTML und HTML5
Was sind die Probleme bei der Verwendung von PHP?
Windows kann nicht auf den freigegebenen Computer zugreifen
Was beinhalten Computersoftwaresysteme?
Befehlstyp für den Linux-Neustart
So verwenden Sie die Dekodierfunktion
Was bedeutet Linux df -h?
