Detaillierte Einführung in den Entscheidungsbaum für maschinelles Lernen in Python-Python-Tutorial-php.cn

Entscheidungsbäume (DTs) sind eine unbeaufsichtigte Lernmethode zur Klassifizierung und Regression.

Vorteile: Die Rechenkomplexität ist nicht hoch, die Ausgabeergebnisse sind leicht zu verstehen, unempfindlich gegenüber fehlenden Zwischenwerten und können irrelevante Merkmalsdaten verarbeiten.
Nachteile: Überanpassungsprobleme können auftreten.
Anwendbar Datentyp: numerischer und nominaler Quellcode-Download https://www.manning.com/books/machine-learning-in-Aktion

Demo ausführen

Schlüsselalgorithmus

if so return class tag;

else

Finden Die besten Funktionen zum Teilen des Datensatzes Funktion
createBranch und Hinzufügen des Rückgabeergebnisses zum Verzweigungsknoten
Verzweigungsknoten zurückgeben
entsprechender Code
def createTree (dataSet,labels):class

List

= [example[-1] for example in dataSet] is not dataset[-1] {the last element of dataset}, und zu diesem Zeitpunkt ist das erste Element vom letzten in jedem Element des Datensatzes

if classList.

count
(classList[0]) == len(classList): Wenn der zurückgegebene klassifizierte Listenanzahltyp ist das gleiche, gib diesen Typ zurück! Ob der untergeordnete Knoten klassifiziert werden kann. Wenn ja, geben Sie einen Typ zurück. Andernfalls rekursiv nach unten klassifizieren == 1: #Aufteilung beenden, wenn keine weiteren Features im DataSet vorhanden sind. Wenn nur ein Element vorhanden ist return MajorityCnt(classList)
bestFeat = ChooseBestFeatureToSplit(dataSet) e = {bestFeatLabel:{}} 　　 Dann erstellen Sie einen Teilbaum der besten Kategorie 　　del( labels[bestFeat])　　 Löschen Sie die beste Kategorie featValues = [example[bestFeat] zum Beispiel in dataSet] uniqueVals = set(featValues) set ist eine Klassifizierung, sehen Sie, wie viele Typen es dafür gibt value in uniqueVals:
subLabels = labels[:] #kopiere alle Labels, damit Bäume vorhandene Labels durcheinander bringen
MyTree [BestFeatlabel] [value] = CreateTree (SPLITDATASET (DataSET, BestFeat, Value), Sublabels
R> R Eturn mytree

Daten Die Änderung der Informationen vor und nach einem Satz wird als Informationsgewinn bezeichnet. Das wichtigste Prinzip beim Teilen eines Datensatzes besteht darin, ungeordnete Daten geordneter zu machen. Dies wird als kuchenschneidendes Prinzip verstanden:

Verwenden Sie die Einheitsentropie, um die Komplexität und Menge an Informationen zu beschreiben. Entsprechend der Dichte des Kuchens, wenn es sich um einen vertikal geschnittenen Kuchen gleicher Dichte handelt,

Das Gewicht jedes Teils g = Gesamt-G * sein Anteil im Großkreis! Wenn analog die Informationsentropie nach der Partitionierung gleich ist, ist das kleine h jedes kleinen Teils der Daten = pro * Gesamt-H und die Summe h[i] = H.

Allerdings: Was wir brauchen, ist Genau das Gegenteil: Es ist nicht so, dass die Informationsentropie gleich ist, aber sie ist ungleich. Die grünen können beispielsweise Grasfüllungen sein, die gelben sind Apfelfüllungen und die blauen sind violette Süßkartoffeln hat eine andere Dichte!

Wir müssen es richtig aufteilen! Sortieren Sie es und finden Sie die Linie, die den verschiedenen Füllungen nahekommt. Das kleine h wird hier minimiert, und schließlich nähert sich das Gesamt-H dem Minimalwert, während die Fläche unverändert bleibt, was ein zu lösendes Optimierungsproblem darstellt.

DebugProcess
calcShannonEnt : [[1, 'no'], [1, 'no']] = 0 log(1, 2) * 0,4 = 0 Warum ist es 0, weil pro 1 sein muss
log(prob,2) log(1,2) = 0;2^0=1, weil prob : [[1, 'ja'], [1, 'ja'], [0, 'nein']] = 0,91 >> * 0,6 = 0,55
25 Zeilen für featVec in dataSet: Häufigkeitszählung für prop
chooseBestFeatureToSplit()　
0.9709505944546686 = calcShannonEnt(dataSet) : [[1, 1, 'yes ' ], [1, 1, 'ja'], [1, 0, 'nein'], [0, 1, 'nein'], [0, 1, 'nein']]

# Erkennung, ob jedes Unterelement des Datensatzes zur gleichen Kategorie gehört: Wenn die Werte alle a sind und die Ergebnisse alle y oder n sind, handelt es sich um eine Kategorie. Daher sind nur zwei Parametereingaben
0,5509775004326937 = += prob * calcShannonEnt(subDataSet) getrennt Nach der Unterteilung wird die Wahrscheinlichkeit * Shannon-Drop, die erhaltene Summe, das ursprüngliche Gesamt-Shannon-Drop-Verhältnis

# 数据越接近，香浓熵值越少，越接近0 ，越不同，越多分逻辑，香浓熵就越大
# 只计算 其dataSet的featVec[-1] 结果标签
def calcShannonEnt(dataSet):

Nach dem Login kopieren

0,4199730940219749 infoGain = baseEntropy - newEntropy

Zusammenfassung: 　

Zuerst konnte ich den Code nicht verstehen und verstand nicht, was er tun sollte! Klassifizierung: Unser Ziel ist es, eine Reihe von Daten zu klassifizieren und mit Etiketten zu kennzeichnen.
Wie k Neighbor Classify([0, 0], Group, Labels, 3), was bedeutet, dass die neuen Daten [0,0] in der Gruppe klassifiziert werden und Daten gemäß dem k=3 Neighbor-Algorithmus beschriftet werden! Gruppe entspricht Label!

Ich habe

später gesehen und dann verstanden, dass der Datensatz die Werte der Dimensionen bedeutet, und der letzte ist, ob es sich um Fisch handelt, Ergebnisbezeichnung 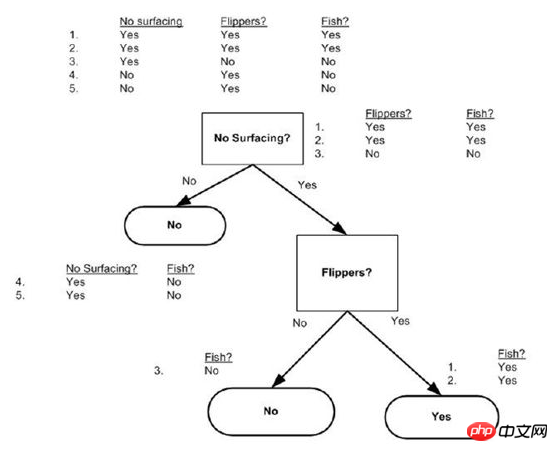Detaillierte Einführung in den Entscheidungsbaum für maschinelles Lernen in Python

Daher ist es notwendig, jede Dimension + Ergebnisbeschriftung in ein zweidimensionales Array auszuschneiden, um sie zu vergleichen und zu klassifizieren.

Der Test sollte darin bestehen, die ersten n Dimensionen zu dividieren. Wert, Vektoreingabe, die Ausgabe ist ja oder nein!

Auf den ersten Blick erscheint es verwirrend, aber es ist einfacher zu verstehen, wenn Sie Ihre Ideen klarstellen und sich den Code ansehen!

Nachdem Sie die Ziel- und Anfangsdaten verstanden haben, werden Sie verstehen, dass classList die Ergebnisbezeichnung ist! , ist das entsprechende Ergebnislabel

, das dem zu klassifizierenden Datensatz entspricht, und labels ist der Feature-Name, der der Dimension des Startdatensatzes entspricht, der Name des Features strname
bestFeatLabel ist der Dimensionsname des Besten Klassifizierungsmerkmal, unabhängig davon, ob es sich um die erste Dimension oder die zweite Dimension handelt, N
featValues ist das Wertearray unter der Dimension von bestFeatLabel. Es sind die Gruppen unter dieser Dimension, die für neue Klassifizierungsvergleiche verwendet werden.
uniqueVals verwendet set, um zu bestimmen, ob es zur gleichen Kategorie gehört,
zum Beispiel
　dataSet = [[1, 1, 'yes'],[0, 1, 'yes'],[1, 0, 'no' ],[1, 0, 'no'],[0, 0, 'no']]
　labels = ['no surfaceing','flippers',]
createTree wie folgt: {'flippers': {0: 'no', 1: 'yes'}} lässt die Dimension „keine Oberfläche“ direkt weg

Schließlich verwenden wir einen Absatz um über den Entscheidungsbaum zu sprechen:

Die Essenz eines Entscheidungsbaums besteht darin, die Effizienz zu beschleunigen! Verwenden Sie „Maximum Optimal“, um das erste negative Etikett zu teilen, und das positive Etikett sollte weiterhin geteilt werden! Und wenn negativ, geben Sie direkt die Antwort des Blattknotens zurück! Die entsprechenden anderen Dimensionen werden nicht weiter bewertet!

Theoretisch können Sie, selbst wenn Sie den Entscheidungsbaumalgorithmus nicht verwenden, alle Daten blind erschöpfen, d. h. jedes Mal alle Dimensionen der Daten durchgehen! Und da ist die letzte Label-Antwort! Anzahl der Dimensionen * Anzahl der Daten! Für Komplexität! Das ist die passende Antwort zur Erinnerung! Passendes Expertensystem! Schlechte Fähigkeit, Situationen vorherzusagen, die nicht eintreten! Aber das Datenvolumen ist groß, die Geschwindigkeit ist hoch und es kann sich auch intelligent anfühlen! Weil es eine Wiederholung vergangener Erfahrungen ist! Aber ist es tot? Nein, es ist nicht tot! Erschöpfung ist tot, aber Entscheidungsbäume sind dynamisch! Lernen! Baum wechseln! Zumindest ist es dynamisch gebaut! Wenn Daten unvollständig sind, können sie auch unvollständig sein! Verwenden Sie ein Urteil, wenn es gelöst werden kann, und wenn nicht, brauchen Sie ein anderes! Abmessungen vergrößert!

Das obige ist der detaillierte Inhalt vonDetaillierte Einführung in den Entscheidungsbaum für maschinelles Lernen in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!