
Ein binärer Suchbaum kann rekursiv wie folgt definiert werden. Ein binärer Suchbaum ist entweder ein leerer Binärbaum oder ein Binärbaum, der die folgenden Eigenschaften erfüllt:
(1) Wenn sein linkes untergeordnetes Element. Wenn der Baum nicht leer ist, ist der Wert des Schlüssels eines beliebigen Knotens in seinem linken Teilbaum kleiner als der Wert des Schlüssels des Wurzelknotens.
(2) Wenn sein rechter Teilbaum nicht leer ist, ist der Wert des Schlüsselworts eines beliebigen Knotens in seinem rechten Teilbaum größer als der Wert des Schlüsselworts des Wurzelknotens.
(3) Seine linken und rechten Teilbäume selbst sind ein binärer Suchbaum.

In Bezug auf die Leistung gilt: Wenn die Anzahl der Knoten im linken und rechten Teilbaum aller Nicht-Blattknoten des binären Suchbaums ungefähr gleich (ausgeglichen) bleibt, dann ist die Suchleistung des binären Suchbaums nahe an der binären Suche , aber ihr Vorteil gegenüber der binären Suche im kontinuierlichen Speicherplatz besteht darin, dass die Struktur des binären Suchbaums geändert wird (Einfügen und Löschen von Knoten). erfordert keine Verschiebung großer Speicherdatensegmente, oft sogar mit konstantem Overhead. Ein binärer Suchbaum kann eine Kombination von Datensätzen darstellen, die in einer sequentiellen Reihenfolge angeordnet sind. Daher wird ein binärer Suchbaum auch als binärer Sortierbaum bezeichnet und derselbe Datensatz kann als verschiedene binäre Suchbäume dargestellt werden. Die Datenstruktur des Knotens des binären Suchbaums ist definiert als:
struct celltype{
records data;
celltype * lchild, * rchild;
}
typedef celltype * BST;In Java ist die Datenstruktur des Knotens wie folgt definiert:
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树中的节点
*/
public class Node {
//存放节点数据
int data;
//指向左子节点
Node left;
//指向右子节点
Node right;
/**
* @function 默认构造函数
* @param data 节点数据
*/
public Node(int data) {
this.data = data;
left = null;
right = null;
}
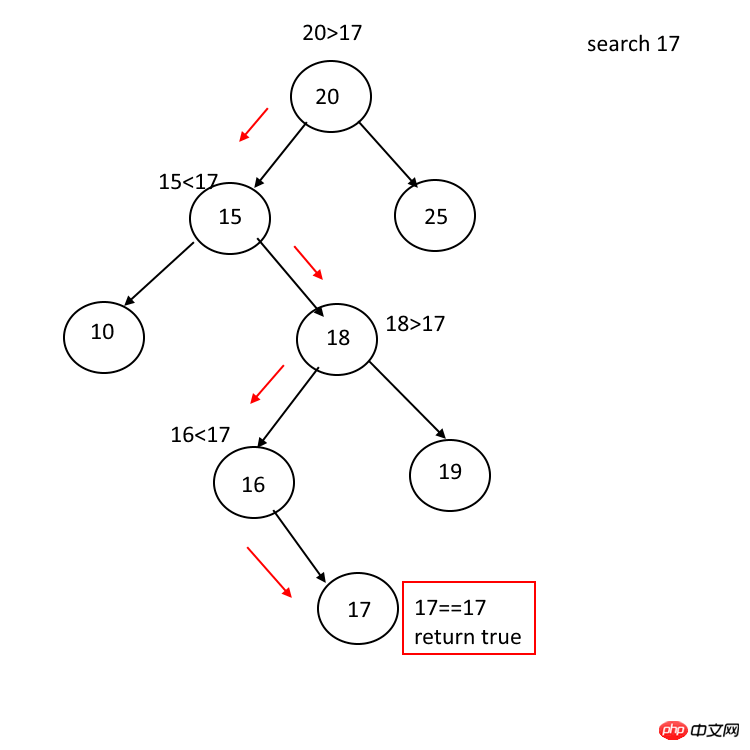
}und Der Suchvorgang des binären Suchbaums beginnt am Wurzelknoten. Wenn das Schlüsselwort der -Abfrage mit dem Schlüsselwort des Knotens übereinstimmt, wird andernfalls ein Treffer erzielt ist kleiner als das Knotenschlüsselwort. Wenn es größer als das Knotenschlüsselwort ist, geben Sie den rechten Sohn ein. Wenn der Zeiger des linken Sohns oder des rechten Sohns leer ist, wird gemeldet, dass das entsprechende Schlüsselwort nicht gefunden werden kann.
BST Search(keytype k, BST F){
//在F所指的二叉查找树中查找关键字为k的记录。若成功,则返回响应结点的指针,否则返回空
if(F == NULL) //查找失败
return NULL;
else if(k == F -> data.key){ //查找成功
return F;
}
else if (k < F -> data.key){ //查找左子树
return Search(k,F -> lchild);
}
else if (k > F -> data.key){ //查找右子树
return Search(k,F -> rchild);
}
}Einen neuen Datensatz R in den binären Suchbaum einfügen. Es sollte sichergestellt werden, dass der binäre Suchbaum nach dem nicht zerstört wird Einfügung. Struktureigenschaften. Um eine Einfügeoperation durchzuführen, sollte man daher zunächst nachschlagen, wo sich R befindet. Bei der Suche wird weiterhin der obige rekursive Algorithmus verwendet. Wenn die Suche fehlschlägt, wird der Knoten, der R enthält, an der Position des leeren Teilbaums eingefügt. Wenn die Suche erfolgreich ist, wird die Einfügung nicht durchgeführt und der Vorgang endet.

void Insert(records R, BST &F){
//在F所指的二叉查找树中插入一个新纪录R
if(F == NULL){
F = new celltype;
F -> data = R;
F -> lchild = NULL;
F -> rchild = NULL;
}
else if (R.key < F -> data.key){
Insert(R,F -> lchild);
}else if(R.key > F -> data.key){
Insert(R,F -> rchild);
}
//如果 R.key == F -> data.key 则返回
}

mit zwei untergeordneten Knoten. Wenn wir eine einfache Ersetzung durchführen, kann die folgende Situation auftreten:

Wir müssen also einen geeigneten Ersatzknoten im Teilbaum auswählen. Der Ersatzknoten ist im Allgemeinen der kleinste Knoten im rechten Teilbaum:

Java-Versionscode-Referenz von BinarySearchTreeBinarySearchTree:
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树的示范代码
*/
public class BinarySearchTree {
//指向二叉搜索树的根节点
private Node root;
//默认构造函数
public BinarySearchTree() {
this.root = null;
}
/**
* @param id 待查找的值
* @return
* @function 默认搜索函数
*/
public boolean find(int id) {
//从根节点开始查询
Node current = root;
//当节点不为空
while (current != null) {
//是否已经查询到
if (current.data == id) {
return true;
} else if (current.data > id) {
//查询左子树
current = current.left;
} else {
//查询右子树
current = current.right;
}
}
return false;
}
/**
* @param id
* @function 插入某个节点
*/
public void insert(int id) {
//创建一个新的节点
Node newNode = new Node(id);
//判断根节点是否为空
if (root == null) {
root = newNode;
return;
}
//设置current指针指向当前根节点
Node current = root;
//设置父节点为空
Node parent = null;
//遍历直到找到第一个插入点
while (true) {
//先将父节点设置为当前节点
parent = current;
//如果小于当前节点的值
if (id < current.data) {
//移向左节点
current = current.left;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.left = newNode;
return;
}
} else {
//否则移向右节点
current = current.right;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.right = newNode;
return;
}
}
}
}
/**
* @param id
* @return
* @function 删除树中的某个元素
*/
public boolean delete(int id) {
Node parent = root;
Node current = root;
//记录被找到的节点是父节点的左子节点还是右子节点
boolean isLeftChild = false;
//循环直到找到目标节点的位置,否则报错
while (current.data != id) {
parent = current;
if (current.data > id) {
isLeftChild = true;
current = current.left;
} else {
isLeftChild = false;
current = current.right;
}
if (current == null) {
return false;
}
}
//如果待删除的节点没有任何子节点
//直接将该节点的原本指向该节点的指针设置为null
if (current.left == null && current.right == null) {
if (current == root) {
root = null;
}
if (isLeftChild == true) {
parent.left = null;
} else {
parent.right = null;
}
}
//如果待删除的节点有一个子节点,且其为左子节点
else if (current.right == null) {
//判断当前节点是否为根节点
if (current == root) {
root = current.left;
} else if (isLeftChild) {
//挂载到父节点的左子树
parent.left = current.left;
} else {
//挂载到父节点的右子树
parent.right = current.left;
}
} else if (current.left == null) {
if (current == root) {
root = current.right;
} else if (isLeftChild) {
parent.left = current.right;
} else {
parent.right = current.right;
}
}
//如果待删除的节点有两个子节点
else if (current.left != null && current.right != null) {
//寻找右子树中的最小值
Node successor = getSuccessor(current);
if (current == root) {
root = successor;
} else if (isLeftChild) {
parent.left = successor;
} else {
parent.right = successor;
}
successor.left = current.left;
}
return true;
}
/**
* @param deleleNode
* @return
* @function 在树种查找最合适的节点
*/
private Node getSuccessor(Node deleleNode) {
Node successsor = null;
Node successsorParent = null;
Node current = deleleNode.right;
while (current != null) {
successsorParent = successsor;
successsor = current;
current = current.left;
}
if (successsor != deleleNode.right) {
successsorParent.left = successsor.right;
successsor.right = deleleNode.right;
}
return successsor;
}
/**
* @function 以中根顺序遍历树
*/
public void display() {
display(root);
}
private void display(Node node) {
//判断当前节点是否为空
if (node != null) {
//首先展示左子树
display(node.left);
//然后展示当前根节点的值
System.out.print(" " + node.data);
//最后展示右子树的值
display(node.right);
}
}
}Testfunktion:
package wx.algorithm.search.bst;
import org.junit.Before;
import org.junit.Test;
/**
* Created by apple on 16/7/30.
*/
public class BinarySearchTreeTest {
BinarySearchTree binarySearchTree;
@Before
public void setUp() {
binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(3);
binarySearchTree.insert(8);
binarySearchTree.insert(1);
binarySearchTree.insert(4);
binarySearchTree.insert(6);
binarySearchTree.insert(2);
binarySearchTree.insert(10);
binarySearchTree.insert(9);
binarySearchTree.insert(20);
binarySearchTree.insert(25);
binarySearchTree.insert(15);
binarySearchTree.insert(16);
System.out.println("原始的树 : ");
binarySearchTree.display();
System.out.println("");
}
@Test
public void testFind() {
System.out.println("判断4是否存在树中 : " + binarySearchTree.find(4));
}
@Test
public void testInsert() {
}
@Test
public void testDelete() {
System.out.println("删除值为2的节点 : " + binarySearchTree.delete(2));
binarySearchTree.display();
System.out.println("\n 删除有一个子节点值为4的节点 : " + binarySearchTree.delete(4));
binarySearchTree.display();
System.out.println("\n 删除有两个子节点的值为10的节点 : " + binarySearchTree.delete(10));
binarySearchTree.display();
}
}Das obige ist der detaillierte Inhalt vonDetaillierte Code-Erklärung der Java-Implementierung des binären Suchbaumalgorithmus (Bild). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




