Detaillierte Erläuterung der Verwendung der Methode der kleinsten Quadrate in Python

Der Grund, warum ich „verwenden“ und nicht „implementieren“ sage, liegt darin, dass die zugehörigen Klassenbibliotheken von Python uns bereits bei der Implementierung bestimmter Algorithmen geholfen haben und wir nur lernen müssen, sie zu verwenden. Mit der allmählichen Beherrschung und Anhäufung der Technologie können wir auch versuchen, verschiedene Algorithmen auf unsere eigene Weise zu implementieren, wenn die Algorithmen in der Klassenbibliothek unsere eigenen Anforderungen nicht mehr erfüllen können.

Kommen wir zurück zum Thema: Was ist die „Methode der kleinsten Quadrate“?

Definition: Die Methode der kleinsten Quadrate (auch bekannt als Methode der kleinsten Quadrate) ist eine mathematische Optimierungstechnik, die die beste Funktionsübereinstimmung der Daten findet, indem sie die Summe der Quadrate der Fehler minimiert.

Funktion: Die Methode der kleinsten Quadrate kann verwendet werden, um unbekannte Daten einfach zu erhalten und die Summe der Quadratfehler zwischen den erhaltenen Daten und den tatsächlichen Daten zu minimieren.

Prinzip: Bestimmen Sie die Position der Geraden durch „Minimieren der Quadratsumme der Residuen“ (in der mathematischen Statistik bezieht sich das Residuum auf die Differenz zwischen dem tatsächlich beobachteten Wert und dem geschätzten Wert)

Grundidee: Für ein univariates lineares Regressionsmodell wird davon ausgegangen, dass n Sätze von Beobachtungswerten (X1, Y1), (X2, Y2), ..., (Xn, Yn) aus der Grundgesamtheit erhalten werden In der Ebene können unzählige Kurven zur Anpassung genutzt werden. Die lineare Regression erfordert, dass die Stichprobenregressionsfunktion so gut wie möglich zu diesem Wertesatz passt. Mit anderen Worten: Diese gerade Linie sollte so zentriert wie möglich in den Stichprobendaten liegen. Daher kann das Kriterium für die Auswahl der besten Anpassungskurve wie folgt bestimmt werden: Minimierung des gesamten Anpassungsfehlers (dh des gesamten Restfehlers).

Der Implementierungscode lautet wie folgt und der Code wurde ausführlich kommentiert:

##最小二乘法
import numpy as np   ##科学计算库 
import scipy as sp   ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt  ##绘图库
from scipy.optimize import leastsq  ##引入最小二乘法算法

'''
     设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])

'''
    设定拟合函数和偏差函数
    函数的形状确定过程：
    1.先画样本图像
    2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''

##需要拟合的函数func :指定函数的形状
def func(p,x):
    k,b=p
    return k*x+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

'''
    主要部分：附带部分说明
    1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
    2.官网的原话（第二个值）：Value of the cost function at the solution
    3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)
    4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost："+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))

'''
   绘图，看拟合效果.
   matplotlib默认不支持中文，label设置中文的话需要另行设置
   如果报错，改成英文就可以
'''

#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) 

#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2) 
plt.legend() #绘制图例
plt.show()

Das Ergebnis lautet wie folgt:

Ausgabeergebnis:

k= 0,900458420439 b= 0,831055638877
Kosten: 1
Die angepasste Gerade ist:
y=0,9x+0,83

Zeichnungsergebnis:

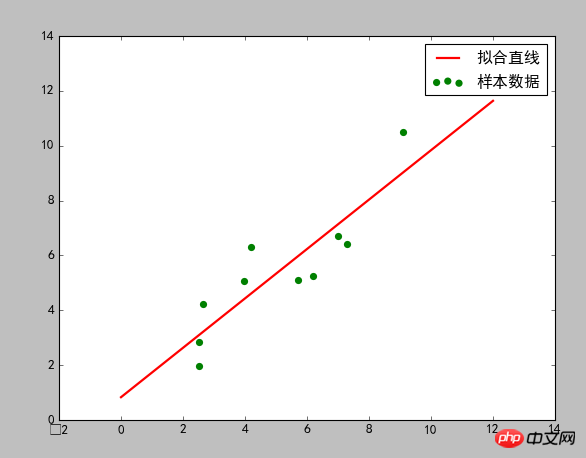
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Verwendung der Methode der kleinsten Quadrate in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!