Codebeispiel für die Implementierung der Hill-Sortierung in Python

Dieser Artikel stellt hauptsächlich die Implementierung der Hill-Sortierung in Python vor. Die programmierte Hill-Sortierung hat einen gewissen Referenzwert.

Beachten Sie die „Einfügungssortierung“: Tatsächlich ist dies nicht schwierig Stellen Sie fest, dass sie einen Mangel hat:

Wenn die Daten „5, 4, 3, 2, 1“ sind, werden wir zu diesem Zeitpunkt die Datensätze im „ungeordneten Block“ in die „mit“-Sequenz einfügen Block "Es wird geschätzt, dass wir abstürzen und die Position jedes Mal verschoben wird, wenn wir einfügen. Zu diesem Zeitpunkt kann man sich die Effizienz der Einfügungssortierung vorstellen.

Die Shell hat den Algorithmus basierend auf dieser Schwäche verbessert und eine Idee namens „reduzierende inkrementelle Sortiermethode“ integriert. Es ist eigentlich ganz einfach, aber es ist zu beachten:

inkrement Es ist nicht zufällig , aber es gibt Regeln, die befolgt werden müssen.

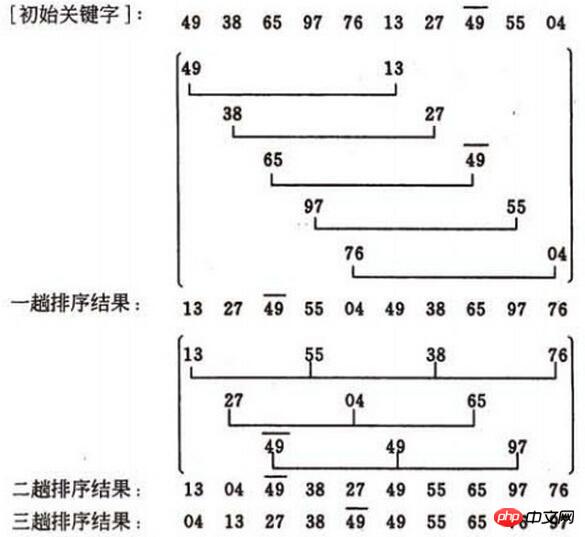
Die Aktualitätsanalyse der Hill-Sortierung ist schwierig. Die Anzahl der Schlüsselcodevergleiche und die Anzahl der Datensatzbewegungen hängen von der Auswahl der Inkrementfaktorsequenz d ab., unter bestimmten Umständen Das Folgende kann die Anzahl der Schlüsselcodevergleiche und die Anzahl der aufgezeichneten Bewegungen genau abschätzen. Bisher hat noch niemand eine Methode zur Auswahl der besten inkrementellen Faktorfolge angegeben. Die inkrementelle Faktorfolge kann auf verschiedene Arten verwendet werden, einschließlich ungerader Zahlen und Primzahlen. Es ist jedoch zu beachten, dass es außer 1 keine gemeinsamen Faktoren zwischen den inkrementellen Faktoren gibt und der letzte inkrementelle Faktor 1 sein muss. Die Hill-Sortiermethode ist eine instabile Sortiermethode. Zuerst müssen wir die Methode der Inkrementierung klären (die Bilder hier stammen aus den Blogs anderer Leute, die Inkrementierung ist eine ungerade Zahl und meine Programmierung unten verwendet eine gerade Zahl):

Das erste Inkrement Die Auswahlmethode ist: d=count/2;

Das zweite Inkrement ist: d=(count/2)/2;

Schließlich geht es zu: d =1;

Okay, achten Sie auf das Bild. Das Inkrement d1=5 im ersten Durchgang teilt die 10 zu sortierenden Datensätze in 5 Teilsequenzen auf Das Ergebnis ist (13, 27, 49, 55, 04, 49, 38, 65, 97, 76)

Der zweite Durchgang erhöht d2=3 und teilt die 10 in die Warteschlange einzureihenden Datensätze in 3 Teilsequenzen auf. bzw. direktes Einfügen durchführen, das Ergebnis ist (13, 04, 49, 38, 27, 49, 55, 65, 97, 76)Das Inkrement d3=1 des dritten Durchgangs, direktes Einfügen Die Sortierung erfolgt für die gesamte Sequenz.

Das Endergebnis

ist (04, 13, 27, 38, 49, 49, 55, 65, 76, 97)Hier kommt der entscheidende Punkt. Wenn das Inkrement auf 1 abnimmt, ist die Reihenfolge grundsätzlich in Ordnung. Der letzte Durchgang der Hill-Sortierung ist die direkte Einfügungssortierung, was der besten Situation nahe kommt. Die „Makro“-Anpassungen in den vorherigen Durchläufen können als Vorverarbeitung des letzten Durchlaufs betrachtet werden, was effizienter ist, als nur eine direkte Einfügungssortierung durchzuführen.

Ich lerne Python und habe heute Python verwendet, um die Hill-Sortierung zu implementieren.

Ausgabe:

def ShellInsetSort(array, len_array, dk): # 直接插入排序
 for i in range(dk, len_array): # 从下标为dk的数进行插入排序
 position = i
 current_val = array[position] # 要插入的数

 index = i
 j = int(index / dk) # index与dk的商
 index = index - j * dk

 # while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 # index = index - dk
 # if 0<=index and index <dk:
 # break

 # position>index,要插入的数的下标必须得大于第一个下标
 while position > index and current_val < array[position-dk]:
 array[position] = array[position-dk] # 往后移动
 position = position-dk
 else:
 array[position] = current_val

def ShellSort(array, len_array): # 希尔排序
 dk = int(len_array/2) # 增量
 while(dk >= 1):
 ShellInsetSort(array, len_array, dk)
 print(">>:",array)
 dk = int(dk/2)

if __name__ == "__main__":
 array = [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
 print(">:", array)
 ShellSort(array, len(array))

Zuallererst müssen Sie die Einfügungssortierung kennen, sonst werden Sie sie definitiv nicht verstehen.

>: [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
>>: [13, 27, 49, 55, 4, 49, 38, 65, 97, 76]
>>: [4, 27, 13, 49, 38, 55, 49, 65, 97, 76]
>>: [4, 13, 27, 38, 49, 49, 55, 65, 76, 97]

Einfügesortierung besteht darin, die Zahlen in die drei gelben Kästchen im Bild oben einzufügen und zu sortieren. Zum Beispiel: 13, 55, 38, 76

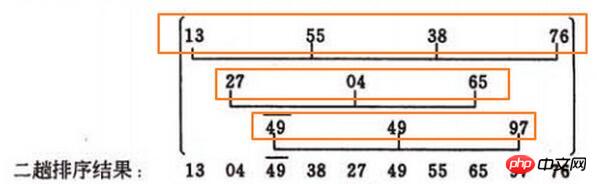Schauen Sie direkt auf 55, 55<13, ohne sich zu bewegen. Schauen Sie sich dann 38, 38<55 an, dann wird 55 nach hinten verschoben und die Daten werden zu [13, 55, 55, 76]. Vergleichen Sie dann 13<38, dann ersetzt 38 55 und wird zu [13, 38, 55, 76]. . Der Rest ist gleich, weggelassen.

Hier gibt es ein Problem, zum Beispiel das zweite gelbe Kästchen

[27, 4, 65], 4<27, dann 27 rückwärts, dann 4 ersetzt das erste und die Daten werden [ 4, 27, 65],

Aber woher weiß der Computer, dass 4 die erste ist?

Mein Ansatz besteht darin, zuerst die erste von [27, 4, 65 zu finden ] Der Index einer Zahl ist in diesem Beispiel der Index von 27. Wenn der Index der einzufügenden Zahl größer als der erste Index ist, kann er nach hinten verschoben werden

Die vorherige Nummer kann nicht nach hinten verschoben werden

, eine davon ist Wenn davor Daten stehen und diese kleiner als die einzufügende Zahl sind, können Sie sie nur danach einfügen. Ein weiterer, sehr wichtiger Punkt: Wenn die einzufügende Zahl kleiner als alle vorherigen Zahlen ist, muss die einzufügende Zahl zuerst platziert werden. Zu diesem Zeitpunkt ist der Index der einzufügenden Zahl = der Index der ersten Zahl. (Diese Passage ist für Anfänger möglicherweise nicht sehr verständlich...) Um den Index der ersten Zahl zu finden, kam mir als Erstes die Verwendung einer Schleife bis ganz nach vorne in den Sinn: Beim Debuggen habe ich festgestellt, dass die Verwendung von Schleifen Zeitverschwendung ist, insbesondere wenn das Inkrement d=1 ist. Um die letzte Zahl direkt in die Liste einzufügen, muss man eine Schleife um 1 durchführen der Index der ersten Zahl. Später wurde ich schlau und verwendete die folgende Methode:

Zeitkomplexität:

while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 index = index - dk
 if 0<=index and index <dk:
 break

Die Zeitkomplexität der Hill-Sortierung ist eine Funktion der verwendeten Inkrementreihenfolge , was schwer genau zu analysieren ist. Einige Literatur weist darauf hin, dass, wenn die inkrementelle Sequenz d[k]=2^(t-k+1) ist, die zeitliche Komplexität der Hill-Sortierung

O(n^1,5),

j = int(index / dk) # index与dk的商
index = index - j * dk

beträgt, wobei t die Sortierzahl ist von Reisen.

Stabilität: Instabil

Hügelsortierungseffekt:

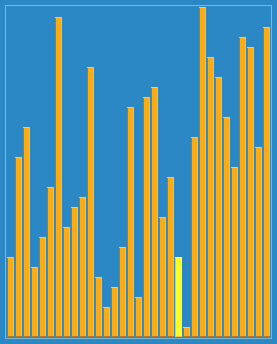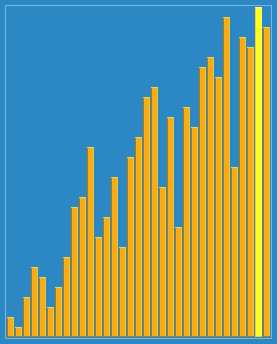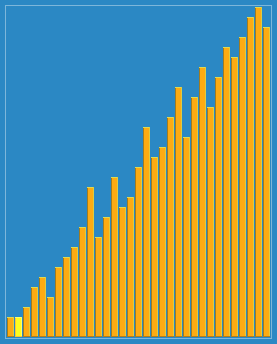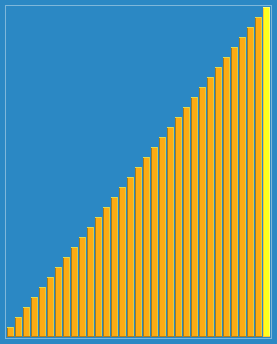
Hinweis: Die Programmierung wird von mir selbst umgesetzt. Es wird empfohlen, den laufenden Prozess zu debuggen und einen Blick darauf zu werfen

Acht wichtige Sortieralgorithmen in C++

Visuelle und intuitive Erfahrung mit mehreren häufig verwendeten Sortieralgorithmen

Sieben Klassische Sortieralgorithmen-Reihe in C# (Teil 2)

1 Nicht-systematisches Lernen ist auch Zeitverschwendung 2. Werden Sie eine technische Person, die Schönheit schätzen, Kunst verstehen und Kunst kennen kann

Das obige ist der detaillierte Inhalt vonCodebeispiel für die Implementierung der Hill-Sortierung in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!