Detaillierte Erklärung gängiger Sortiercodes in Python

In diesem Artikel wird hauptsächlich das grundlegende Tutorial des Python-Algorithmus ausführlich vorgestellt, das einen gewissen Referenzwert hat.

Vorwort: Der schriftliche Test von Tencent hat in den ersten beiden Tagen 10.000 Punkte erhalten. Ich habe das Gefühl, dass ich zwei Tage damit verschwendet habe, zu Niuke.com zu gehen und die Fragen zu beantworten ... In diesem Blog werden mehrere einfache/allgemeine Sortieralgorithmen vorgestellt, die aussortiert werden.

Zeitliche Komplexität

(1) ZeithäufigkeitDie Zeit, die zur Ausführung eines Algorithmus benötigt wird, kann nicht theoretisch berechnet werdenSie müssen den Test durchführen auf Ihrer Maschine, um es zu wissen. Aber es ist für uns unmöglich und unnötig, jeden Algorithmus auf dem Computer zu testen. Wir müssen nur wissen, welcher Algorithmus mehr Zeit benötigt und welcher weniger Zeit benötigt. Und die Zeit, die ein Algorithmus benötigt, ist proportional zur Anzahl der Ausführungen von Anweisungen im Algorithmus. Je nachdem, welcher Algorithmus mehr Anweisungen hat, benötigt er mehr Zeit. Die Anzahl der Anweisungsausführungen in einem Algorithmus wird als Anweisungshäufigkeit oder Zeithäufigkeit bezeichnet. Bezeichnen Sie es als T(n).

(2) Zeitkomplexität In der gerade erwähnten Zeitfrequenz wird n als Maßstab des Problems bezeichnet. Wenn sich n weiterhin ändert, ändert sich auch die Zeitfrequenz T(n). . Aber manchmal möchten wir wissen, welches Muster es zeigt, wenn es sich ändert. Zu diesem Zweck führen wir das Konzept der Zeitkomplexität ein. Im Allgemeinen ist die Häufigkeit, mit der die Grundoperationen im Algorithmus wiederholt werden, eine Funktion der Problemgröße n, dargestellt durch T(n), wenn es eine Hilfsfunktion f(n) gibt n nähert sich der Unendlichkeit, der Grenzwert von T(n)/f(n) ist eine Konstante , die ungleich Null ist, dann heißt f(n) eine Funktion in der gleichen Größenordnung wie T( N). Mit der Bezeichnung T(n)=O(f(n)) wird O(f(n)) als asymptotische Zeitkomplexität des Algorithmus oder kurz Zeitkomplexität bezeichnet.

Exponentielle Zeit

bezieht sich auf die Berechnungszeit m(n), die zur Lösung eines Problems erforderlich ist, abhängig von der Größe des Problems Eingabedaten Und es wächst exponentiell (das heißt, die Menge der Eingabedaten wächst linear und die aufgewendete Zeit wird exponentiell wachsen)

for (i=1; i<=n; i++)
 x++;
for (i=1; i<=n; i++)
 for (j=1; j<=n; j++)
 x++;

Die Zeit des ersten für Schleife ist komplex Der Grad ist Ο(n), die Zeitkomplexität der zweiten for-Schleife ist Ο(n2), dann ist die Zeitkomplexität des gesamten Algorithmus Ο(n+n2)=Ο(n2).

Konstante Zeit

Wenn die Obergrenze eines Algorithmus unabhängig von der Eingabegröße ist, spricht man von einer konstanten Zeit, die als bezeichnet wird Zeit. Ein Beispiel ist der Zugriff auf ein einzelnes Element in einem Array, da für den Zugriff nur eine Anweisung erforderlich ist. Das Finden des kleinsten Elements in einem ungeordneten Array ist jedoch nicht möglich, da dazu eine Schleife durch alle Elemente erforderlich ist, um den kleinsten Wert zu finden. Dies ist eine lineare Zeitoperation oder Zeit. Wenn jedoch die Anzahl der Elemente im Voraus bekannt ist und angenommen wird, dass die Anzahl konstant bleibt, kann man auch sagen, dass die Operation eine konstante Zeit hat.

Logarithmische Zeit

Wenn der Algorithmus

T(n) =O(logn), dann It Es wird gesagt, dass es eine logarithmische Zeit hat

Zu den gängigen Algorithmen mit

logarithmischer Zeit gehören Operationen im Zusammenhang mit Binärbäumen und die binäre Suche.

Der logarithmische Zeitalgorithmus ist sehr effizient, da mit jeder zusätzlichen Eingabe die zusätzlich benötigte Rechenzeit kleiner wird.

Das rekursive Zerteilen einer Zeichenfolge in zwei Hälften und die Ausgabe ist ein einfaches Beispiel für eine Funktion in dieser Kategorie. Es dauert O(log n) Zeit, da wir die Zeichenfolge vor jeder Ausgabe halbieren. Das heißt, wenn wir die Anzahl der Ausgänge erhöhen wollen, müssen wir die Stringlänge verdoppeln.

Lineare Zeit

Wenn die

Zeitkomplexität eines Algorithmus O(n) ist, dann wird der Algorithmus als linear bezeichnet Zeit oder O(n)-Zeit. Informell bedeutet dies, dass bei ausreichend großen Eingaben die Laufzeit linear mit der Größe der Eingabe zunimmt. Beispielsweise benötigt ein Programm, das die Summe aller Elemente einer Liste berechnet, proportional zur Länge der Liste Zeit.

1. Blasenalgorithmus

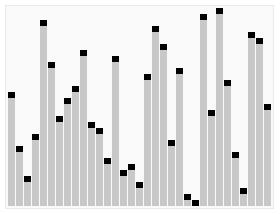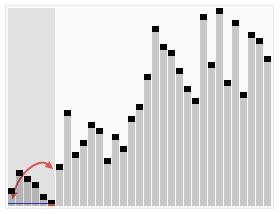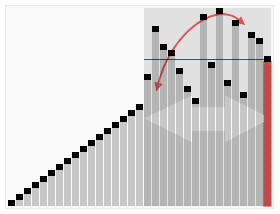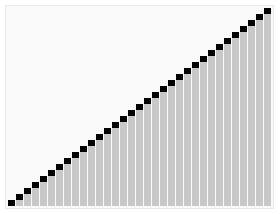
Grundidee:

In einer zu sortierenden Zahlengruppe wurde das aktuelle Paar nicht sortiert Dennoch werden alle Zahlen innerhalb des Sequenzbereichs von oben nach unten verglichen und angepasst, sodass die größere Zahl sinkt und die kleinere Zahl steigt. Das heißt: Immer wenn zwei benachbarte Zahlen verglichen werden und sich herausstellt, dass sie in der entgegengesetzten Reihenfolge zu den Reihenfolgeanforderungen sind, werden sie vertauscht.

Beispiel für Blasensortierung:

Algorithmusimplementierung:

def bubble(array):
 for i in range(len(array)-1):
 for j in range(len(array)-1-i):
 if array[j] > array[j+1]: # 如果前一个大于后一个，则交换
 temp = array[j]
 array[j] = array[j+1]
 array[j+1] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print("------->排序前<-------")
 print(array)
 bubble(array)
 print("------->排序后<-------")
 print(array)

Ausgabe:

------->Vor dem Sortieren<-------

[265, 494, 302, 160, 370, 219, 247, 287, 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
------->Nach dem Sortieren<-- --- --
[82, 83, 160, 219, 247, 258, 265, 287, 291, 302, 304, 319, 345, 354, 370, 405, 423, 469, 494, 497]

Erklärung:

以随机产生的五个数为例:　li=[354,405,469,82,345]
冒泡排序是怎么实现的?
首先先来个大循环，每次循环找出最大的数，放在列表的最后面。在上面的例子中，第一次找出最大数469，将469放在最后一个，此时我们知道
列表最后一个肯定是最大的，故还需要再比较前面4个数，找出4个数中最大的数405，放在列表倒数第二个......

5个数进行排序，需要多少次的大循环??　当然是4次啦!同理，若有n个数，需n-1次大循环。

现在你会问我: 第一次找出最大数469，将469放在最后一个??怎么实现的??
嗯，（在大循环里）用一个小循环进行两数比较，首先354与405比较，若前者较大，需要交换数；反之不用交换。
当469与82比较时，需交换，故列表倒数第二个为469；469与345比较，需交换，此时最大数469位于列表最后一个啦!

难点来了，小循环需要多少次??

进行两数比较，从列表头比较至列表尾，此时需len(array)-1次!! 但是，嗯，举个例子吧: 当大循环i为3时，说明此时列表的最后3个数已经排好序了，不必进行两数比较，故小循环需len(array)-1-3.　即len(array)-1-i

冒泡排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

简单选择排序的示例：

二、选择排序

The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example

基本思想：

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

简单选择排序的示例：

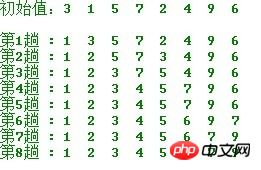
算法实现:

def select_sort(array):
 for i in range(len(array)-1): # 找出最小的数放与array[i]交换
 for j in range(i+1, len(array)):
 if array[i] > array[j]:
 temp = array[i]
 array[i] = array[j]
 array[j] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print(array)
 select_sort(array)
 print(array)

选择排序复杂度:

时间复杂度: 最好情况O(n^2), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 不稳定

举个例子：序列5 8 5 2 9， 我们知道第一趟选择第1个元素5会与2进行交换，那么原序列中两个5的相对先后顺序也就被破坏了。

排序效果：

三、直接插入排序

插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

插入排序非常类似于整扑克牌。

在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。

也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

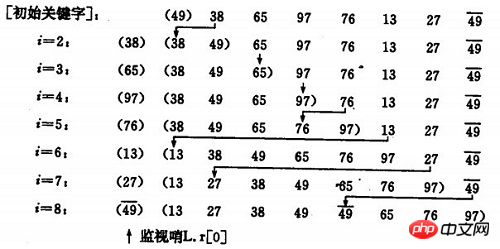
设监视哨是我大一在书上有看过，大家忽视上图的监视哨。

算法实现:

import time


def insertion_sort(array):
 for i in range(1, len(array)): # 对第i个元素进行插入，i前面是已经排序好的元素
 position = i # 要插入数的下标
 current_val = array[position] # 把当前值存下来
 # 如果前一个数大于要插入数，则将前一个数往后移，比如5,8,12,7;要将7插入，先把7保存下来，比较12与7，将12往后移
 while position > 0 and current_val < array[position-1]:
 array[position] = array[position-1]
 position -= 1
 else: # 当position为０或前一个数比待插入还小时
 array[position] = current_val


if __name__ == "__main__":
 array = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
 print(array)
 time_start = time.time()
 insertion_sort(array)
 time_end = time.time()
 print("time: %s" % (time_end-time_start))
 print(array)

输出:

[92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
time: 0.0
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

直接插入排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

个人感觉直接插入排序算法难度是选择/冒泡算法是两倍……

四、快速排序

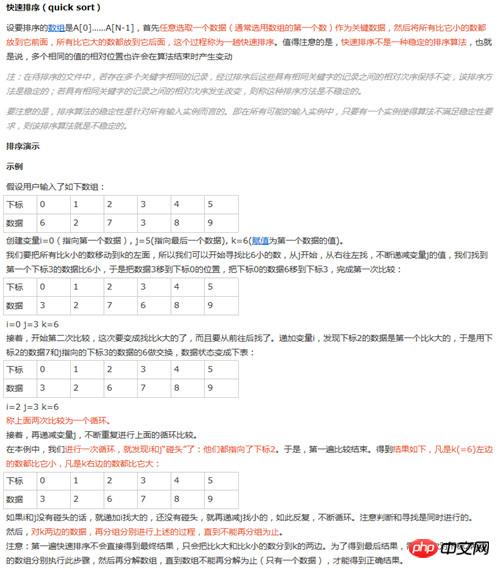
快速排序示例:

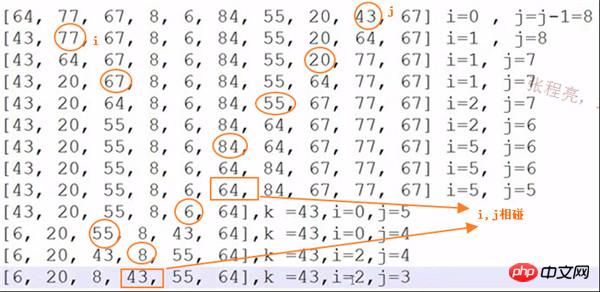
算法实现:

def quick_sort(array, left, right):
 '''
 :param array:
 :param left: 列表的第一个索引
 :param right: 列表最后一个元素的索引
 :return:
 '''
 if left >= right:
 return

 low = left
 high = right
 key = array[low] # 第一个值，即基准元素

 while low < high: # 只要左右未遇见
 while low < high and array[high] > key: # 找到列表右边比key大的值 为止
 high -= 1
 # 此时直接 把key跟 比它大的array[high]进行交换
 array[low] = array[high]
 array[high] = key

 while low < high and array[low] <= key: # 找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
 low += 1
 # 找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
 array[high] = array[low]
 array[low] = key

 quick_sort(array, left, low-1) # 最后用同样的方式对分出来的左边的小组进行同上的做法
 quick_sort(array,low+1, right) # 用同样的方式对分出来的右边的小组进行同上的做法


if __name__ == &#39;__main__&#39;:
 array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
 print("-------排序前-------")
 print(array)
 quick_sort(array, 0, len(array)-1)
 print("-------排序后-------")
 print(array)

输出:

-------排序前-------
[8, 4, 1, 14, 6, 2, 3, 9, 5, 13, 7, 1, 8, 10, 12]
-------排序后-------
[1, 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, 12, 13, 14]

22行那里如果不加＝号，当排序64，77，64是会死循环，此时key=64,　最后的64与开始的64交换，开始的64与本最后的64交换……　无穷无尽

直接插入排序复杂度:

时间复杂度: 最好情况O(nlogn), 最坏情况O(n^2), 平均情况O(nlogn)

下面空间复杂度是看别人博客的，我也不大懂了……改天再研究下。

最优的情况下空间复杂度为：O(logn)；每一次都平分数组的情况

最差的情况下空间复杂度为：O( n )；退化为冒泡排序的情况

稳定性:不稳定

快速排序效果：

Das obige ist der detaillierte Inhalt vonDetaillierte Erklärung gängiger Sortiercodes in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!