Teilen Sie ein Beispiel, bei dem die Anzahl der Ziffern in js zu groß ist, was zum Verlust der Parametergenauigkeit führt.

Teilen Sie ein Beispiel, bei dem die Anzahl der Ziffern in js zu groß ist, was zum Verlust der Parametergenauigkeit führt

Bei der Übergabe eines Parameters bin ich kürzlich auf ein seltsames Problem gestoßen Bei einer js-Funktion wird ein Bit übergeben. Wenn Sie Argumente ausgeben, können Sie sehen, dass sich die übergebenen Parameter geändert haben.

Dann habe ich nachgesehen und festgestellt, dass es tatsächlich durch den Verlust der js-Präzision verursacht wurde. Meine Lösung besteht darin, die Übertragung vom numerischen Typ auf den Zeichentyp umzustellen, damit die Genauigkeit nicht verloren geht. Wie unten gezeigt:

Der Grund, warum JS-Zahlen an Präzision verlieren

Die binäre Implementierung des Computers und die Anzahl der Ziffernbeschränkungen . Manche Zahlen können nicht endlich dargestellt werden. Genauso wie einige irrationale Zahlen nicht endlich dargestellt werden können, wie zum Beispiel pi 3,1415926..., 1,3333... usw. JS entspricht IEEE 754-Spezifikation, mit doppelter Präzisionsspeicherung (doppelte Präzision) und Belegung von 64 Bit. Wie in der Abbildung gezeigt

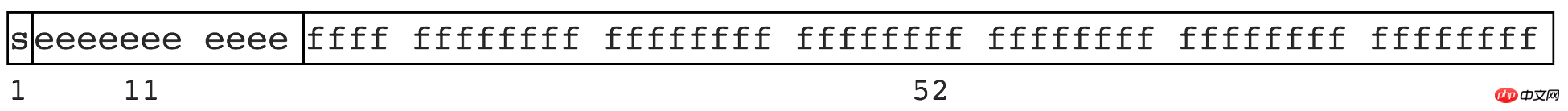
Bedeutung

• 1 Bit wird zur Darstellung des Vorzeichenbits verwendet

• 11 Bits werden verwendet, um den Exponenten darzustellen

• 52 Bits stellen die Mantisse dar

Gleitkommazahl, wie z. B.

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

kann zu diesem Zeitpunkt nur verwendet werden. Die Rundung wird durchgeführt, um die Dezimalzahl zu imitieren, aber die Binärzahl hat nur zwei Zahlen: 0 und 1, sodass sie zu 0 wird und auf 1 gerundet wird. Dies ist die Hauptursache für Fehler und Genauigkeitsverluste bei einigen Gleitkommazahloperationen in Computern.

Der Präzisionsverlust großer Ganzzahlen ist im Wesentlichen derselbe wie der von Gleitkommazahlen. Die maximale Anzahl von Mantissenstellen beträgt 52, sodass die größte Ganzzahl, die in JS genau dargestellt werden kann, Math.pow(2, 53), was in der Dezimalzahl 9007199254740992 ist.

Größer als 9007199254740992 kann an Genauigkeit verlieren

9007199254740992     >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

Tatsächlich

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

Das Ergebnis ist wie in der Abbildung dargestellt

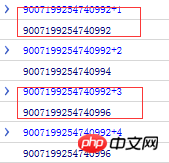
Aus dem oben Gesagten können wir erkennen, dass die scheinbar endlichen Zahlen in der Binärdarstellung des Computers tatsächlich unendlich sind. Aufgrund der Begrenzung der Anzahl der Speicherstellen kommt es zu einer „Rundung“ und einem Verlust an Präzision auftritt.

想了解更深入的分析可以看这篇论文（又长又臭）：What Every Computer Scientist Should Know About Floating-Point Arithmetic

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

Das obige ist der detaillierte Inhalt vonTeilen Sie ein Beispiel, bei dem die Anzahl der Ziffern in js zu groß ist, was zum Verlust der Parametergenauigkeit führt.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!