Der vollständige Name des KNN-Algorithmus lautet k-Nearest Neighbor, was K nächster Nachbar bedeutet.
Algorithmusbeschreibung
KNN ist ein Klassifizierungsalgorithmus. Seine Grundidee besteht darin, durch Messung des Abstands zwischen verschiedenen Merkmalswerten zu klassifizieren.
Der Algorithmusprozess ist wie folgt:
1 Bereiten Sie den Beispieldatensatz vor (jeder Datenwert in der Probe wurde klassifiziert und verfügt über ein Klassifizierungsetikett). Daten für das Training:
4. Berechnen Sie den Abstand zwischen A und den einzelnen Daten.
6 der Abstand von A Die kleinsten k Punkte; Berechnen Sie die Häufigkeit des Auftretens der ersten k Punkte. Geben Sie die Kategorie mit der höchsten Häufigkeit des Auftretens der ersten k Punkte zurück vorhergesagte Klassifizierung von A.
Hauptfaktoren
Trainingssatz (oder Beispieldaten)
Wenn der Trainingssatz zu klein ist, kommt es zu Fehleinschätzungen. Wenn der Trainingssatz zu groß ist, entsteht ein Systemaufwand Die Klassifizierung der Testdaten wird sehr groß sein.
Distanz (oder ähnlicher Messalgorithmus)
Was ist ein geeignetes Distanzmaß? Ein geringerer Abstand sollte bedeuten, dass die beiden Punkte mit größerer Wahrscheinlichkeit zur gleichen Kategorie gehören.
Entfernungsmessungen umfassen:
1. Euklidische Distanz
Euklidische Metrik (auch Euklidische Distanz genannt) ist eine häufig verwendete Distanzdefinition und bezieht sich auf die tatsächliche Distanz zwischen zwei Punkten in m-dimensionaler Raum oder die natürliche Länge des Vektors (d. h. der Abstand vom Punkt zum Ursprung). Der euklidische Abstand im zwei- und dreidimensionalen Raum ist der tatsächliche Abstand zwischen zwei Punkten.
Geeignet bei Platzproblemen.
2. Manhattan-Distanz
Taxigeometrie oder Manhattan-Distanz ist ein von Herman Minkowski im 19. Jahrhundert geschaffener Begriff. Es handelt sich um eine Art geometrischer metrischer Raum, der in verwendet wird Summe der absoluten Achsabstände zweier Punkte im Standardkoordinatensystem. Der Manhattan-Abstand ist die Summe der Abstände der Projektionen der durch den euklidischen Abstand gebildeten Liniensegmente auf dem festen rechtwinkligen Koordinatensystem des euklidischen Raums auf der Achse.
Die rote Linie im Bild stellt die Manhattan-Entfernung dar, die grüne stellt die euklidische Entfernung dar, also die geradlinige Entfernung, und die blaue und die gelbe Linie stellen die entsprechende Manhattan-Entfernung dar Distanz. Manhattan-Entfernung – die Entfernung zwischen zwei Punkten in Nord-Süd-Richtung plus die Entfernung in Ost-West-Richtung, d. h. d(i, j) = |xi-xj|+|yi-yj|.
Geeignet für Wegprobleme.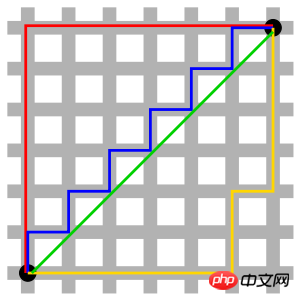 
3. Tschebyscheff-Distanz
In der Mathematik ist die Tschebyscheff-Distanz ein Maß im Vektorraum. Der Abstand zwischen zwei Punkten ist der absolute Unterschied im numerischen Wert jeder Koordinate .
Die Tschebyscheff-Distanz wird verwendet, um die Entfernung zwischen zwei Punkten im Raster zu berechnen, z. B. bei Schachbrett-, Lager- und Logistikanwendungen.
Für ein Gitter ist ein Punkt, dessen Tschebyscheff-Distanz 1 ist, die Moore-Umgebung dieses Punktes.
wird für Probleme bei der Berechnung von Entfernungen in einem Raster verwendet.
4. Minkowski-Distanz 
Min-Distanz ist keine Distanz, sondern die Definition einer Reihe von Distanzen.
Abhängig von den verschiedenen variablen Parametern kann die Min-Distanz eine Art Distanz darstellen.
Es gibt einen variablen Parameter p in der Formel:
Wenn p=1, ist es die Manhattan-Distanz;
Wenn p=2, ist es die euklidische Distanz; Das ist die Tschebyscheff-Distanz.
5. Standardisierte euklidische Distanz
Standardisierte euklidische Distanz ist ein Verbesserungsschema, das die Mängel der einfachen euklidischen Distanz beseitigt und als gewichtete euklidische Distanz betrachtet werden kann.
Die Idee des euklidischen Standardabstands: Da die Verteilung jeder Dimensionskomponente der Daten unterschiedlich ist, „standardisieren“ Sie zunächst jede Komponente, um den gleichen Mittelwert und die gleiche Varianz zu haben.
6. Mahalanobis-Distanz
stellt die Kovarianzdistanz der Daten dar.
Es ist eine effektive Methode zur Berechnung der Ähnlichkeit zweier unbekannter Stichprobensätze.
Dimensionsunabhängig, wodurch die Interferenz der Korrelation zwischen Variablen beseitigt werden kann.
7. Bhattacharyya-Distanz In der Statistik wird die Bhattacharyya-Distanz zur Messung zweier diskreter Wahrscheinlichkeitsverteilungen verwendet. Es wird häufig bei der Klassifizierung verwendet, um die Trennbarkeit zwischen Klassen zu messen.
8. Hamming-Distanz (Hamming-Distanz)
Die Hamming-Distanz zwischen zwei Saiten gleicher Länge s1 und s2 ist definiert als der minimale Arbeitsaufwand, der erforderlich ist, um eine von ihnen in die andere zu verwandeln. Anzahl der Auswechslungen.
Zum Beispiel beträgt der Hamming-Abstand zwischen den Zeichenfolgen „1111“ und „1001“ 2.
Anwendung:
Informationskodierung (um die Fehlertoleranz zu erhöhen, sollte der minimale Hamming-Abstand zwischen Codes so groß wie möglich gemacht werden).
9. Kosinus des eingeschlossenen Winkels (Cosinus)
In der Geometrie kann der Kosinus des eingeschlossenen Winkels verwendet werden, um die Richtungsdifferenz zweier Vektoren zu messen, und beim Data Mining kann Es kann verwendet werden, um die Differenz zwischen Probenvektoren zu messen.
10. Jaccard-Ähnlichkeitskoeffizient (Jaccard-Ähnlichkeitskoeffizient)
Der Jaccard-Abstand misst die Unterscheidung zwischen zwei Mengen, indem er den Anteil unterschiedlicher Elemente in allen Elementen in den beiden Mengen verwendet.
Der Jaccard-Ähnlichkeitskoeffizient kann verwendet werden, um die Ähnlichkeit von Proben zu messen.
11. Pearson-Korrelationskoeffizient
Der Pearson-Korrelationskoeffizient, auch Pearson-Produkt-Moment-Korrelationskoeffizient genannt, ist ein linearer Korrelationskoeffizient. Der Pearson-Korrelationskoeffizient ist eine Statistik, die den Grad der linearen Korrelation zwischen zwei Variablen widerspiegelt.
Der Einfluss hoher Dimensionen auf die Distanzmessung:
Wenn mehr Variablen vorhanden sind, wird die Unterscheidungsfähigkeit der euklidischen Distanz schlechter.
Der Einfluss des Variablenbereichs auf die Distanz:
Variablen mit größeren Wertebereichen spielen bei Distanzberechnungen oft eine dominierende Rolle, daher sollten die Variablen zunächst standardisiert werden.
Die Größe von k
k ist zu klein, die Klassifizierungsergebnisse werden leicht durch Rauschpunkte beeinflusst und der Fehler nimmt zu
k ist zu groß und die nächsten Nachbarn können es sein Zu viele Punkte anderer Kategorien einbeziehen (die Gewichtung des Abstands kann die Auswirkung der k-Wert-Einstellung verringern);
k=N (Anzahl der Stichproben) ist völlig unerwünscht, da es einfach ist, was die Eingabeinstanz zu diesem Zeitpunkt ist Vorausgesagt, dass es zur Trainingsklasse mit den meisten Instanzen gehört, ist das Modell zu einfach und ignoriert viele nützliche Informationen in den Trainingsinstanzen.
In praktischen Anwendungen nimmt der K-Wert normalerweise einen relativ kleinen Wert an. Beispielsweise wird die Kreuzvalidierungsmethode verwendet (einfach ausgedrückt werden einige Proben als Trainingssatz und andere als Test verwendet). eingestellt), um den optimalen K-Wert auszuwählen.
Faustregel: k ist im Allgemeinen kleiner als die Quadratwurzel der Anzahl der Trainingsbeispiele.
Vorteile und Nachteile
1. Vorteile
Einfach, leicht zu verstehen, leicht zu implementieren, hohe Genauigkeit und unempfindlich gegenüber Ausreißern.
2. Nachteile
KNN ist ein Lazy-Algorithmus. Es ist sehr einfach, ein Modell zu erstellen, aber der Systemaufwand für die Klassifizierung von Testdaten ist groß (großer Rechenaufwand und großer Speicheraufwand). , weil es alle Trainingsbeispiele scannen und die Entfernung berechnen muss.
Anwendbarer Bereich
Numerischer Typ und Nominaltyp (mit einer endlichen Anzahl verschiedener Werte und ungeordneten Werten).
Zum Beispiel Kundenabwanderungsvorhersage, Betrugserkennung usw.
Algorithmusimplementierung
Hier nehmen wir Python als Beispiel, um die Implementierung des KNN-Algorithmus basierend auf der euklidischen Distanz zu beschreiben.
Formel für den euklidischen Abstand:
Beispielcode am Beispiel des euklidischen Abstands:
#! /usr/bin/env python#-*- coding:utf-8 -*-# E-Mail : Mike_Zhang@live.comimport mathclass KNN: def __init__(self,trainData,trainLabel,k):
self.trainData = trainData
self.trainLabel = trainLabel
self.k = k def predict(self,inputPoint):
retLable = "None"arr=[]for vector,lable in zip(self.trainData,self.trainLabel):
s = 0for i,n in enumerate(vector) :
s += (n-inputPoint[i]) ** 2arr.append([math.sqrt(s),lable])
arr = sorted(arr,key=lambda x:x[0])[:self.k]
dtmp = {}for k,v in arr :if not v in dtmp : dtmp[v]=0
dtmp[v] += 1retLable,_ = sorted(dtmp.items(),key=lambda x:x[1],reverse=True)[0] return retLable
data = [
[1.0, 1.1],
[1.0, 1.0],
[0.0, 0.0],
[0.0, 0.1],
[1.3, 1.1],
]
labels = ['A','A','B','B','A']
knn = KNN(data,labels,3)print knn.predict([1.2, 1.1])
print knn.predict([0.2, 0.1])Nach dem Login kopieren
Der Die obige Implementierung ist relativ einfach. Sie können in der Entwicklung vorgefertigte Bibliotheken verwenden, z. B. scikit-learn:
Algorithmusanwendung
Das obige ist der detaillierte Inhalt vonDetaillierte Einführung in den KNN-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
