JAVA-Sortierung Heap-Sortierung
Der Editor unten zeigt Ihnen einen altmodischen Vergleich der Heap-Sortierung. Der Herausgeber findet es ziemlich gut, deshalb werde ich es jetzt mit Ihnen teilen und es allen als Referenz geben. Folgen wir dem Editor, um einen Blick darauf zu werfen.
Für die Heap-Sortierung sind umfassende Binärbaumkenntnisse erforderlich. Betrachten Sie die zu sortierende Sequenz {10, 2, 11, 8, 7} als vollständigen Binärbaum, wie in der folgenden Abbildung dargestellt.
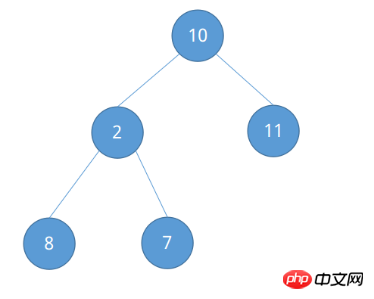
Der Heap ist in einen großen Root-Heap und einen kleinen Root-Heap unterteilt: Der große Root-Heap bedeutet, dass jeder Root-Knoten größer ist als seine untergeordneten Knoten (L(i)) >= L(2i) && L(i) >= L(2i + 1)), der kleine Root-Heap bedeutet, dass jeder Root-Knoten kleiner ist als sein untergeordneter Knoten (L(i) <= L(2i) && L(i) <= L( 2i + 1)). (In einem vollständigen Binärbaum ist der linke untergeordnete Knoten des i-ten Knotens 2i und sein rechter Byteknoten ist 2i + 1)
In diesem Artikel wird die Konstruktion von a erläutert großer Root-Heap als Beispiel.
Der erste Schritt beim Heap-Sortieren – der Aufbau des anfänglichen Heaps. Wie erstellt man den anfänglichen Heap? Per Definition liegt der Schlüsselpunkt in jedem Wurzelknoten. Wenn man den vollständigen Binärbaum der oben genannten zu sortierenden Sequenz betrachtet, ist es nicht schwer festzustellen, dass Knoten 2 und Knoten 10 untergeordnete Knoten haben, bei denen es sich um Knoten handelt, die Aufmerksamkeit erfordern.
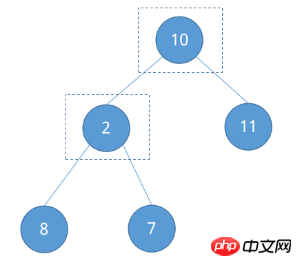
Wie finde ich Knoten 2? Es wird festgestellt, dass es sich um einen Blattknoten oder den übergeordneten Knoten des letzten Knotens handelt. Gemäß den Eigenschaften eines vollständigen Binärbaums beträgt die Nummer des übergeordneten Knotens jedes Knotens mit Ausnahme des Wurzelknotens ⌊n / 2⌋. Da n = 5 ist, ist es leicht zu erkennen, dass die Anzahl von Knoten 2 ⌊5 / 2⌋ = ② ist. Vergleichen Sie es mit der Größe des linken und rechten untergeordneten Knotens und passen Sie es an.
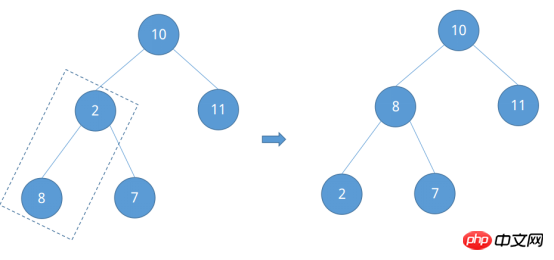
Schließlich bleibt der Wurzelknoten 10 übrig. Es ist bekannt, dass die Nummer des Knotens 2 ②, ② - 1 = ① ist, was die Nummer des Wurzelknotens 10 bedeutet erhalten wird. Vergleichen Sie es mit der Größe des linken und rechten untergeordneten Knotens und passen Sie es an.
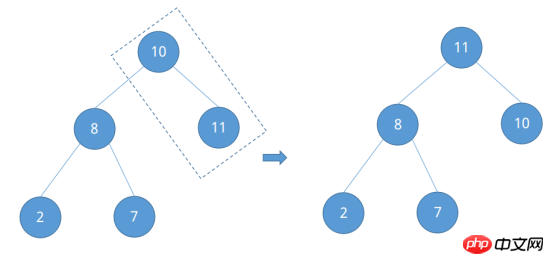
Nachdem die Anpassung abgeschlossen ist, wird festgestellt, dass ein „großer Wurzelhaufen“ gebildet wurde. Die zu sortierende Spalte ist im Beispiel relativ einfach und mehr Die zu sortierende komplexe Spalte wird gegeben, um ihren Prozess des Aufbaus eines großen Wurzelhaufens zu beobachten. Behandeln Sie die zu sortierende Sequenz {53, 17, 78, 09, 45, 65, 87, 32} als vollständigen Binärbaum.
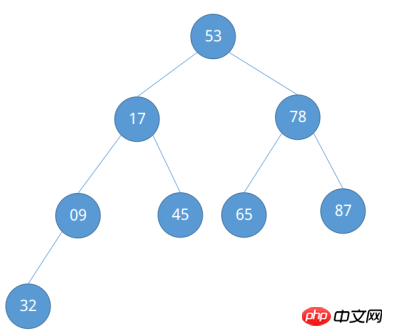
Schauen wir uns in ähnlicher Weise die Knoten an, auf die geachtet werden muss.
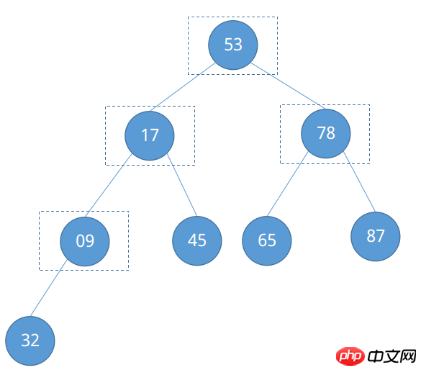
Gemäß dem ersten Beispiel können wir die Nummer des Knotens 09 leicht als ⌊8 / 2⌋ = ④ und die Nummer des Knotens 78 als ④ - 1 = ermitteln ③… ... und so weiter wird ein bestimmtes Muster gefunden, das heißt, die Knotenposition, die für angepasst werden muss, stammt von ⌊n / 2⌋ Beginnen Sie mit der schrittweisen Abnahme bis zum Ende des Wurzelknotens ① (⌊n / 2⌋ ~ 1). Beginnen Sie jetzt mit der Anpassung.
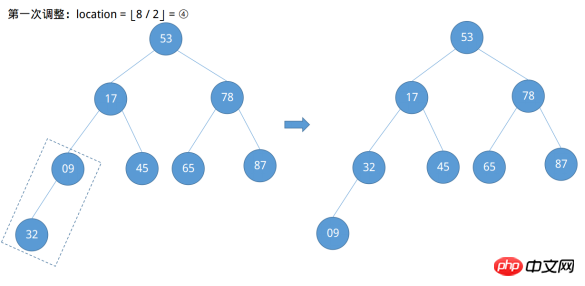
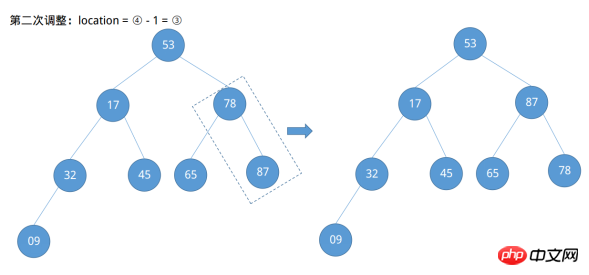
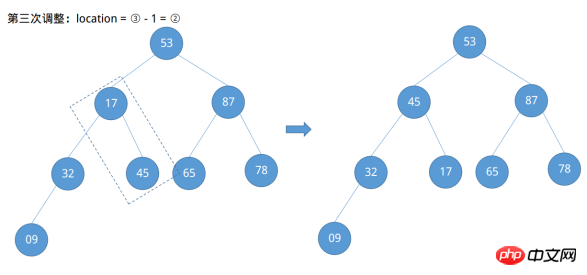
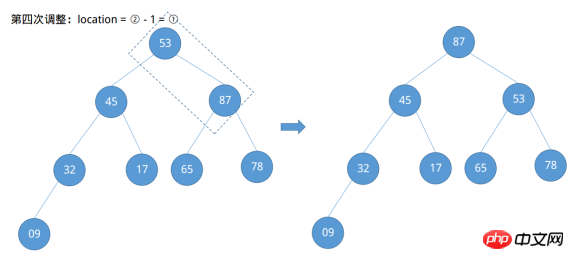
Entdeckt nach der vierten Anpassung, die Knoten 53 tut Erfüllt nicht die Definition eines großen Root-Heaps und sein rechter untergeordneter Knoten ist größer. Zu diesem Zeitpunkt ist eine weitere Anpassung nach unten erforderlich.
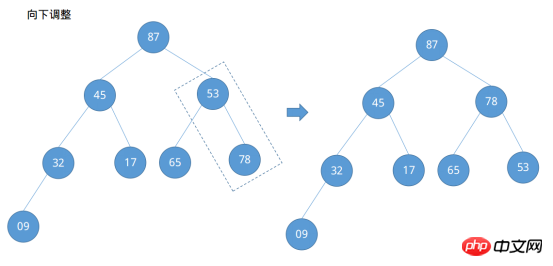
Beachten Sie, dass jedes Mal, wenn eine Aufwärtsanpassung vorgenommen wird, Abwärtsanpassungen vorgenommen werden müssen, um festzustellen, ob eine Abwärtsanpassung erforderlich ist, anstatt nach Abschluss aller Aufwärtsanpassungen zurückzublicken. Nach unten anpassen. Auf diese Weise wird ein großer Root-Heap erstellt und die Situation des zu sortierenden Spaltenarrays hat sich geändert: {87, 45, 78, 32, 17, 65, 53, 09}. Als nächstes stellt sich die Frage, wie sortiert werden soll. Tauschen Sie den Wurzelknoten des großen Root-Heaps mit dem letzten Knoten aus und passen Sie den Binärbaum so an, dass er weiterhin den großen Root-Heap erfüllt.
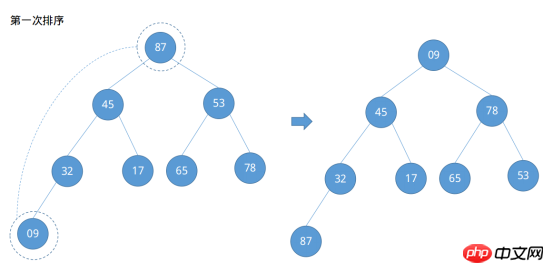
Sie können sehen, dass nach dem Aufrufen des Wurzelknotens und des letzten Knotens der Maximalwert der zu sortierenden Spalte an der letzten Position des Arrays {..., 87} platziert wurde. Zu diesem Zeitpunkt der erste Die Sortierung ist abgeschlossen, aber dieser erste Durchgang ist noch nicht abgeschlossen. Zu diesem Zeitpunkt erfüllen die anderen Knoten mit Ausnahme von Knoten 87 nicht die Bedingungen des großen Root-Heaps, sodass die verbleibenden Knoten an den großen Root-Heap angepasst werden müssen Haufen. Der Sortiervorgang ist nicht mehr gegeben. Die Code-Implementierung in Java und Python3 ist wie folgt.
Java
package com.algorithm.sort.heap;
import java.util.Arrays;
/**
* 堆排序
* Created by yulinfeng on 6/20/17.
*/
public class Heap {
public static void main(String[] args) {
int[] nums = {53, 17, 78, 09, 45, 65, 87, 32};
nums = heapSort(nums);
System.out.println(Arrays.toString(nums));
}
/**
* 堆排序
* @param nums 待排序数组序列
* @return 排好序的数组序列
*/
private static int[] heapSort(int[] nums) {
for (int i = nums.length / 2 - 1; i >= 0; i--) {
heapAdjust(nums, i, nums.length);
}
for (int i = nums.length - 1; i > 0; i--) {
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
heapAdjust(nums, 0, i);
}
return nums;
}
/**
* 调整堆
*
* @param nums 待排序序列
* @param parent 待调整根节点
* @param length 数组序列长度
*/
private static void heapAdjust(int[] nums, int parent, int length) {
int temp = nums[parent];
int childIndex = 2 * parent + 1; //完全二叉树节点i从编号1开始的左子节点位置在2i,此处数组下标从0开始,即左子节点所在数组索引位置为:2i + 1
while (childIndex < length) {
if (childIndex + 1 < length && nums[childIndex] < nums[childIndex + 1]) {
childIndex++; //节点有右子节点,且右子节点大于左子节点,则选取右子节点
}
if (temp > nums[childIndex]) {
break; //如果选中节点大于其子节点,直接返回
}
nums[parent] = nums[childIndex];
parent = childIndex;
childIndex = 2 * parent + 1; //继续向下调整
}
nums[parent] = temp;
}
}Python3
#堆排序
def heap_sort(nums):
for i in range(int(len(nums) / 2 - 1), -1, -1):
heap_adjust(nums, i, len(nums))
for i in range(len(nums) - 1, -1, -1):
temp = nums[i]
nums[i] = nums[0]
nums[0] = temp
heap_adjust(nums, 0, i)
return nums
#调整堆
def heap_adjust(nums, parent, length):
temp = nums[parent]
childIndex = 2 * parent + 1
while childIndex < length:
if childIndex + 1 < length and nums[childIndex] < nums[childIndex + 1]:
childIndex += 1
if temp > nums[childIndex]:
break
nums[parent] = nums[childIndex]
parent = childIndex
childIndex = 2 * parent + 1
nums[parent] = temp
nums = [53, 17, 78, 09, 45, 65, 87, 32]
nums = heap_sort(nums)
print(nums)Die obige Klischee-Vergleichssortierung und Heap-Sortierung ist der gesamte vom Herausgeber geteilte Inhalt. Ich hoffe, dass er Ihnen eine Referenz geben kann, und ich hoffe, dass Sie Script Home unterstützen.
Das obige ist der detaillierte Inhalt vonJAVA-Sortierung Heap-Sortierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1389
1389
 52
52
 Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur perfekten Zahl in Java. Hier besprechen wir die Definition, Wie prüft man die perfekte Zahl in Java?, Beispiele mit Code-Implementierung.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden für Weka in Java. Hier besprechen wir die Einführung, die Verwendung von Weka Java, die Art der Plattform und die Vorteile anhand von Beispielen.
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4
 Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Gestalten Sie die Zukunft: Java-Programmierung für absolute Anfänger
Oct 13, 2024 pm 01:32 PM
Java ist eine beliebte Programmiersprache, die sowohl von Anfängern als auch von erfahrenen Entwicklern erlernt werden kann. Dieses Tutorial beginnt mit grundlegenden Konzepten und geht dann weiter zu fortgeschrittenen Themen. Nach der Installation des Java Development Kit können Sie das Programmieren üben, indem Sie ein einfaches „Hello, World!“-Programm erstellen. Nachdem Sie den Code verstanden haben, verwenden Sie die Eingabeaufforderung, um das Programm zu kompilieren und auszuführen. Auf der Konsole wird „Hello, World!“ ausgegeben. Mit dem Erlernen von Java beginnt Ihre Programmierreise, und wenn Sie Ihre Kenntnisse vertiefen, können Sie komplexere Anwendungen erstellen.




