Detaillierte Erläuterung des Beispiels für den PHP-Heap-Sortieralgorithmus

Dieser Artikel stellt hauptsächlich den in PHP implementierten Heap-Sortieralgorithmus vor und analysiert die Prinzipien, Implementierungsschritte und zugehörigen Betriebstechniken der PHP-Heap-Sortierung in Form von Beispielen

Die Beispiele in diesem Artikel beschreiben den in PHP implementierten Heap-Sortieralgorithmus. Ich möchte es Ihnen als Referenz mitteilen:

Erfahrung

Ich habe im Vorstellungsgespräch gearbeitet Bei der Firma, für die ich gearbeitet habe, war ich vom technischen Aspekt schockiert. Nein, denn meine Kenntnisse über Datenstruktur und andere Grundlagen sind wirklich dürftig, obwohl ich ursprünglich Designer werden wollte. . . Da ich jedoch ganz gut PHP schreiben kann, kann ich ein Praktikum absolvieren, bin aber trotzdem fest entschlossen, die Grundlagen aufzufrischen. Tatsächlich habe ich schon früher gespürt, wie wichtig die Grundlagen sind. Einige tiefere Dinge sind relativ niedrig und es gibt keine Möglichkeit, fortzufahren, ohne sie gut zu lernen. Ich habe zum Beispiel vorher PHP verwendet, um Websockets zu erstellen, bei denen es um Konzepte wie Datenpakete und Datenrahmen ging, die ich nicht verstehen konnte und die ich später nicht einmal verarbeiten musste. Deshalb werde ich grundlegende Kenntnisse wie Datenstrukturen, Algorithmen und Netzwerke neu erlernen. Ich möchte auch alle daran erinnern, nicht wie ich in die entgegengesetzte Richtung zu gehen. Es wird sogar zu spät sein, bis Sie es verstanden haben.

Lassen Sie uns heute über das Problem der Heap-Sortierung sprechen, das gefragt wurde. Als ich danach gefragt wurde, vergaß ich sogar das Konzept eines vollständigen Binärbaums. Glücklicherweise verfüge ich immer noch über ein wenig Grundwissen über die Datenstruktur und verstehe es einigermaßen, nachdem ich einige Informationen gelesen habe. Deshalb möchte ich PHP verwenden, um eine Art Heap-Binärbaum zu schreiben, und nebenbei überprüfe ich auch Binärbäume, Heaps und andere Datenstrukturen.

Heap

Heap ist ein allgemeiner Begriff für eine spezielle Art von Datenstruktur in der Informatik. Normalerweise handelt es sich um eine Datenstruktur Das kann ein Array-Objekt sein, das als Baum betrachtet wird.

Haufen {k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

Über den Heap:

Der Wert eines Knotens im Heap ist immer Nicht größer oder kleiner als der Wert seines übergeordneten Knotens.
Der Heap ist immer ein vollständiger Binärbaum (unten).
Der Heap mit dem größten Wurzelknoten wird als maximaler Heap oder großer Root-Heap bezeichnet, und der Heap mit dem kleinsten Wurzelknoten wird als minimaler Heap oder kleiner Root-Heap bezeichnet.

Vollständiger Binärbaum

Wenn es um Heap-Sortierung geht, müssen wir vollständige Binärbäume erwähnen Im Internet habe ich mir das einfachste ausgesucht. .

Vollständiger Binärbaum: Mit Ausnahme der letzten Ebene erreicht die Anzahl der Knoten auf jeder Ebene das Maximum; auf der letzten Ebene fehlen nur einige Knoten auf der rechten Seite.

Ich bin zu dem Schluss gekommen, dass dies genau an den folgenden zwei Merkmalen liegt:

1 Nur die letzte Ebene darf freie Knoten haben und die Leerstellen befinden sich auf der rechten Seite , die Blattknoten können nur auf den beiden größten Ebenen erscheinen (Regelmäßigkeit der Speichermethode); ;

macht das Sortieren sehr bequem.

Heap-Sortierung

Heap-Sortierung verwendet den großen oberen Heap für aufsteigende Reihenfolge und den kleinen oberen Heap für absteigende Reihenfolge.

In diesem Beispiel wird zur Analyse ein kleiner oberer Heap in absteigender Reihenfolge verwendet.

Die Schritte für die Heap-Sortierung sind wie folgt:

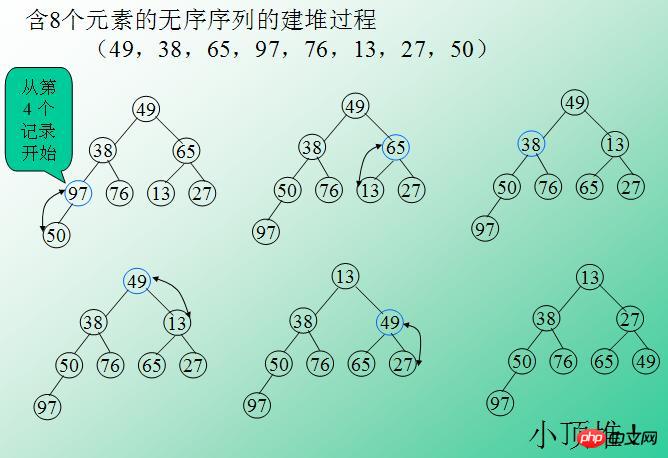
1 Wir erstellen ein Array $arr aus den Daten (49, 38, 65, 97, 76, 13 , 27, 50) ;

2. Verwenden Sie das Array $arr, um einen kleinen oberen Heap zu erstellen (die Hauptschritte werden in den Codekommentaren erläutert. Die folgende Abbildung zeigt den Prozess der Verwendung eines Arrays zum Erstellen eines kleinen oberen Heaps );
3. Ändern Sie die Wurzel des Heaps (Das kleinste Element) wird mit dem letzten Blatt ausgetauscht, und die Heap-Länge wird um eins reduziert und zum zweiten Schritt gesprungen; 3, bis nur noch ein Knoten im Heap vorhanden ist und die Sortierung abgeschlossen ist.

PHP-Implementierung der Heap-Sortierung

Folgendes ist das Endergebnis der Sortierung:

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2;
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);
//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);
for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);
}
//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
  //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
  //从$index处对一个树进行循环比较,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左节点,将其下标存进最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }
    }
  }
}
//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Beispiels für den PHP-Heap-Sortieralgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!