
In diesem Artikel werden hauptsächlich die grundlegenden, häufig verwendeten Sortieralgorithmen in Javascript ausführlich vorgestellt, die einen gewissen Referenzwert haben.
Hinweis: Der größte Teil des Inhalts wird aus dem Internet kopiert Der Code ist von Hand selbst zu schreiben. Es handelt sich lediglich um einen Rückblick auf die Vergangenheit und neues Wissen, nicht um Originalität.
1. Bubble Sort
(1) Algorithmusbeschreibung
Bubble Sort ist ein einfacher Sortieralgorithmus. Es durchläuft wiederholt die zu sortierende Sequenz, vergleicht jeweils zwei Elemente und vertauscht sie, wenn sie in der falschen Reihenfolge sind. Der Besuch des Arrays wird wiederholt, bis kein Austausch mehr erforderlich ist, was bedeutet, dass das Array sortiert wurde. Der Name dieses Algorithmus rührt von der Tatsache her, dass kleinere Elemente durch den Austausch langsam an die Spitze des Arrays „schweben“.
(2) Algorithmusbeschreibung und Implementierung
Der spezifische Algorithmus wird wie folgt beschrieben:
<1>. Wenn das erste größer als das zweite ist, tauschen Sie beide aus; <2> Machen Sie dasselbe für jedes Paar benachbarter Elemente, vom ersten Paar am Anfang bis zum letzten Paar am Ende, sodass das letzte Element Es sollte die größte Zahl sein; <3>. Wiederholen Sie die Schritte 1–3 für alle Elemente, bis die Sortierung abgeschlossen ist.
JavaScript-Code-Implementierung:

Verbesserte Blasensortierung: Legen Sie eine ikonische Variable pos fest, um die Position des letzten Austauschs in jedem Sortierdurchlauf aufzuzeichnen. Da die Datensätze nach der Pos-Position vertauscht wurden, muss beim nächsten Sortierdurchgang nur noch die Pos-Position gescannt werden.
Der verbesserte Algorithmus lautet wie folgt:

Bei der herkömmlichen Blasensortierung kann jeder Sortiervorgang nur einen Maximal- oder Minimalwert finden. Wir erwägen die Verwendung der Methode Durch die Durchführung von Vorwärts- und Rückwärtsblasen in jedem Sortierdurchgang können zwei Endwerte (der größte und der kleinste) gleichzeitig erhalten werden, wodurch die Anzahl der Sortierdurchgänge um fast die Hälfte reduziert wird.
Der verbesserte Algorithmus ist:

Die Laufzeit der drei Algorithmen beträgt:
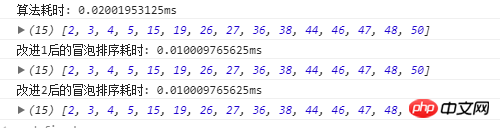
Aus den Laufergebnissen ist ersichtlich, dass die zeitliche Komplexität geringer und der Zeitverbrauch kürzer ist. Sie können es selbst ausprobieren. Es ist am besten, die drei Algorithmen beim Ausführen in eine Datei zu schreiben, da sonst aufgrund von Browsern und anderen Gründen Fehler auftreten.
Dynamische Diagrammdemonstration der Blasensortierung:
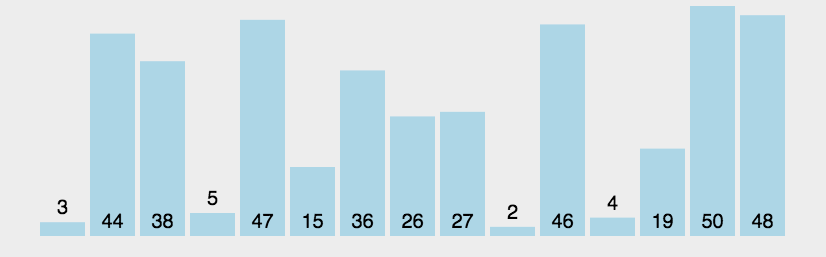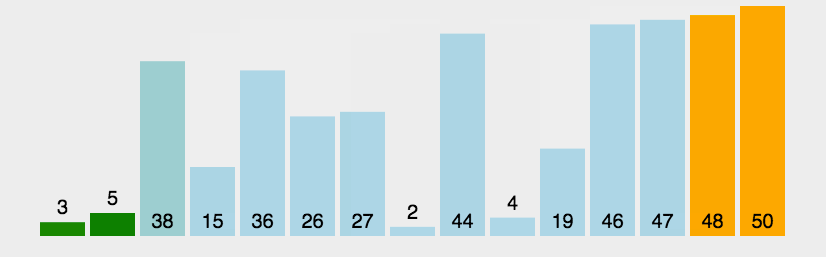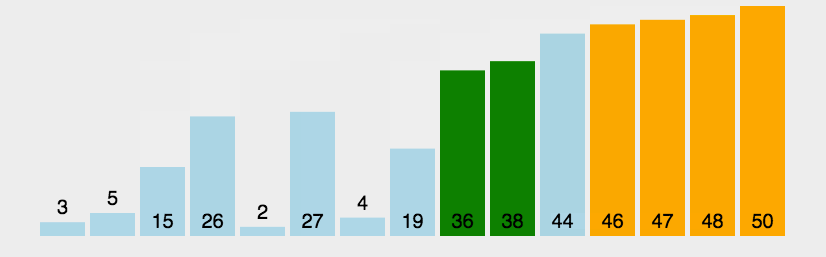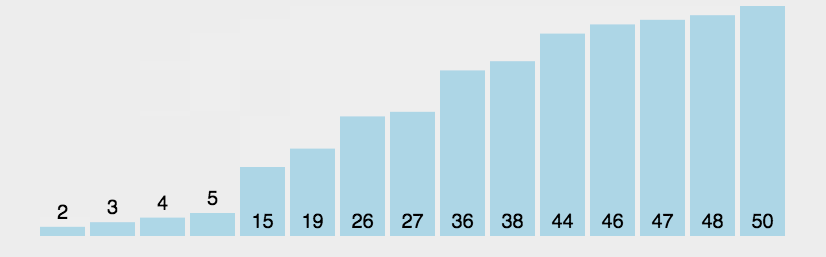
(3) Algorithmusanalyse
Bester Fall: T(n) = O (n )
Wenn die Eingabedaten bereits in positiver Reihenfolge vorliegen
Schlimmster Fall: T(n) = O(n2)
Wenn die Eingabedaten in umgekehrter Reihenfolge vorliegen
Durchschnittsfall: T(n) = O(n2)
2. Der stabilste Sortieralgorithmus Eins, denn egal welche Daten eingegeben wird, beträgt die zeitliche Komplexität O(n²). Bei der Verwendung gilt also: Je kleiner die Datengröße, desto besser. Der einzige Vorteil besteht möglicherweise darin, dass kein zusätzlicher Speicherplatz belegt wird. Theoretisch ist die Auswahlsortierung möglicherweise auch die häufigste Sortiermethode, an die die meisten Menschen beim Sortieren denken.
(1) Einführung in den Algorithmus Selection-Sort ist ein einfacher und intuitiver Sortieralgorithmus. So funktioniert es: Suchen Sie zunächst das kleinste (große) Element in der unsortierten Sequenz und speichern Sie es an der Startposition der sortierten Sequenz. Suchen Sie dann weiterhin das kleinste (große) Element aus den verbleibenden unsortierten Elementen und fügen Sie es dann ein in die sortierte Reihenfolge. Und so weiter, bis alle Elemente sortiert sind. (2) Beschreibung und Implementierung des Algorithmus Durch die Direktauswahlsortierung von n Datensätzen können geordnete Ergebnisse durch n-1 Direktauswahlsortierdurchgänge erzielt werden. Der spezifische Algorithmus wird wie folgt beschrieben: <1>. Der ungeordnete Bereich ist R[1..n], der geordnete Bereich ist leer; 1,2,3...n-1) Zu Beginn sind der aktuelle geordnete Bereich und der ungeordnete Bereich R[1..i-1] bzw. R(i..n). Diese Sortieroperation wählt den Datensatz R[k] mit dem kleinsten Schlüssel aus dem aktuellen ungeordneten Bereich aus und tauscht ihn mit dem ersten Datensatz R im ungeordneten Bereich aus, sodass R[1..i] und R[i+1 .. n) werden jeweils ein neuer geordneter Bereich mit einer um 1 erhöhten Anzahl von Datensätzen und ein neuer ungeordneter Bereich mit einer um 1 verringerten Anzahl von Datensätzen. Der n-1-Durchlauf endet und das Array ist geordnet. Javascript-Code-Implementierung: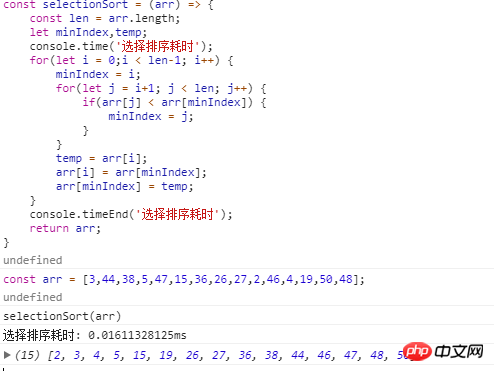
(3) Algorithmusanalyse 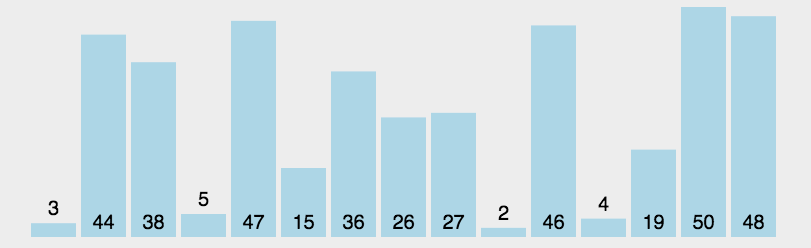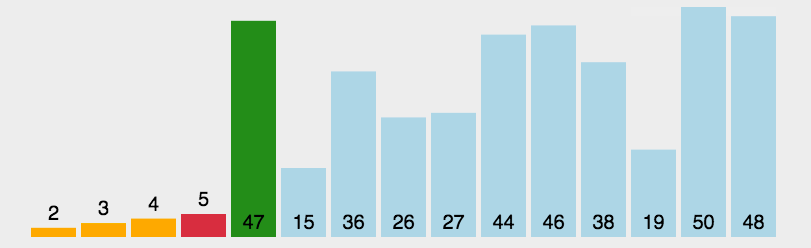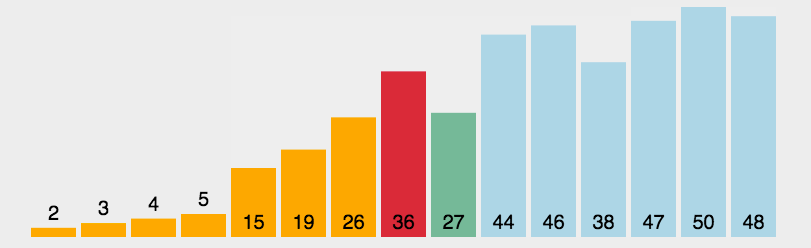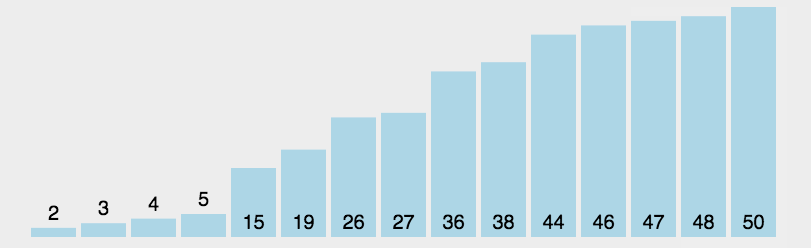
Das obige ist der detaillierte Inhalt vonBeispielanalyse grundlegender, häufig verwendeter Sortieralgorithmen in JavaScript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




